Een regelmatige veelhoek is een 2-dimensionale convexe figuur met congruente zijden en gelijke hoeken in maat. Veel polygonen, zoals vierhoeken of driehoeken, hebben eenvoudige formules om hun gebieden te vinden, maar als u met een polygoon werkt die meer dan vier zijden heeft, kunt u het beste een formule gebruiken die het apothema en de omtrek van de vorm gebruikt. Met een beetje moeite kunt u het gebied met reguliere polygonen in slechts een paar minuten vinden.
Deel een van de twee:
Het gebied berekenen
-
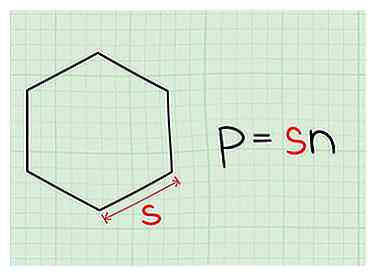 1 Bereken de omtrek. De omtrek is de gecombineerde lengte van de omtrek van een tweedimensionaal figuur. Voor een regelmatige polygoon kan deze worden berekend door de lengte van één zijde te vermenigvuldigen met het aantal zijden (n).[1]
1 Bereken de omtrek. De omtrek is de gecombineerde lengte van de omtrek van een tweedimensionaal figuur. Voor een regelmatige polygoon kan deze worden berekend door de lengte van één zijde te vermenigvuldigen met het aantal zijden (n).[1] -
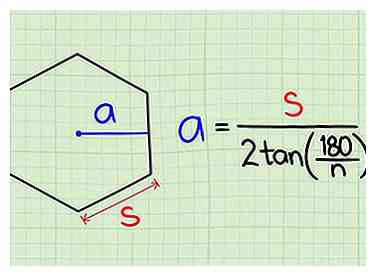 2 Bepaal de apothem. De afstand van een regelmatige veelhoek is de kortste afstand van het middelpunt tot één van de zijden, waardoor een rechte hoek ontstaat. Dit is een beetje lastiger om te berekenen dan de omtrek.
2 Bepaal de apothem. De afstand van een regelmatige veelhoek is de kortste afstand van het middelpunt tot één van de zijden, waardoor een rechte hoek ontstaat. Dit is een beetje lastiger om te berekenen dan de omtrek. - De formule voor het berekenen van de lengte van de apothem is deze: de lengte van de zijde (s) gedeeld door 2 maal de tangens (tan) van 180 graden gedeeld door het aantal zijden (n).
-
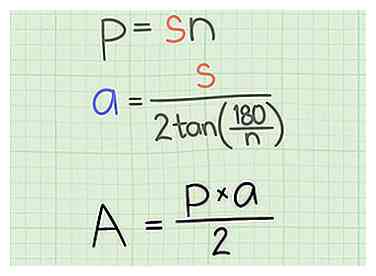 3 Ken de juiste formule. Het gebied van elke regelmatige veelhoek wordt gegeven door de formule: Gebied = (een X p)/2, waar een is de lengte van de apothem en p is de omtrek van de veelhoek.
3 Ken de juiste formule. Het gebied van elke regelmatige veelhoek wordt gegeven door de formule: Gebied = (een X p)/2, waar een is de lengte van de apothem en p is de omtrek van de veelhoek. -
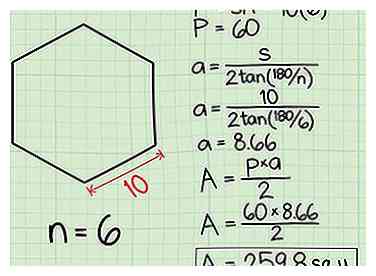 4 Sluit de waarden van een en p in de formule en haal het gebied op. Laten we als voorbeeld een zeskant (6 zijden) gebruiken met een zijde (s) lengte van 10.
4 Sluit de waarden van een en p in de formule en haal het gebied op. Laten we als voorbeeld een zeskant (6 zijden) gebruiken met een zijde (s) lengte van 10. - De omtrek is 6 x 10 (n X s), gelijk aan 60 (dus p = 60).
- De apothem wordt berekend door zijn eigen formule, door 6 en 10 aan te sluiten voor n en s. Het resultaat van 2tan (180/6) is 1.1547 en dan is 10 gedeeld door 1.1547 gelijk aan 8.66.
- Het gebied van de polygoon is Gebied = een X p / 2, of 8,66 vermenigvuldigd met 60 gedeeld door 2. De oplossing is een oppervlakte van 259,8 eenheden.
- Merk ook op dat er geen haakjes staan in de vergelijking "Gebied", dus 8,66 gedeeld door 2 vermenigvuldigd met 60, geven hetzelfde resultaat, net als 60 gedeeld door 2 vermenigvuldigd met 8,66 geeft hetzelfde resultaat.
Deel twee van twee:
De concepten op een andere manier begrijpen
-
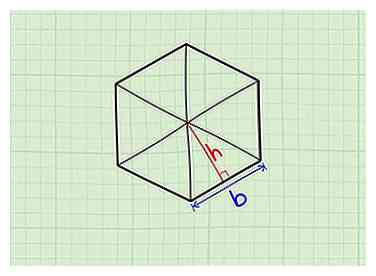 1 Begrijp dat een regelmatige polygoon kan worden beschouwd als een verzameling driehoeken. Elke zijde vertegenwoordigt de basis van een driehoek en er zijn evenveel driehoeken in de veelhoek als er zijden zijn. Elk van de driehoeken is gelijk in basislengte, hoogte en oppervlakte.[2]
1 Begrijp dat een regelmatige polygoon kan worden beschouwd als een verzameling driehoeken. Elke zijde vertegenwoordigt de basis van een driehoek en er zijn evenveel driehoeken in de veelhoek als er zijden zijn. Elk van de driehoeken is gelijk in basislengte, hoogte en oppervlakte.[2] -
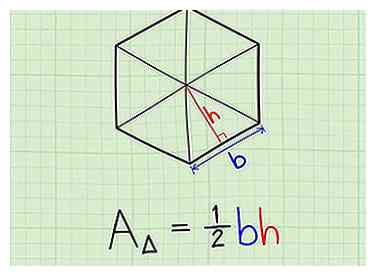 2 Denk aan de formule voor het gebied van een driehoek. Het gebied van een willekeurige driehoek is 1/2 keer de lengte van de basis (die in de veelhoek de lengte van een zijde is) vermenigvuldigd met de hoogte (die hetzelfde is als de apotheker in regelmatige veelhoek).[3]
2 Denk aan de formule voor het gebied van een driehoek. Het gebied van een willekeurige driehoek is 1/2 keer de lengte van de basis (die in de veelhoek de lengte van een zijde is) vermenigvuldigd met de hoogte (die hetzelfde is als de apotheker in regelmatige veelhoek).[3] -
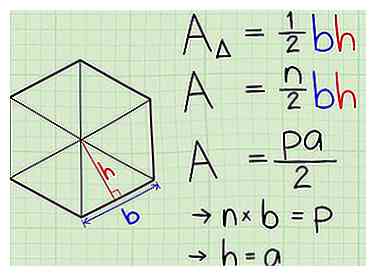 3 Zie de overeenkomsten. Nogmaals, de formule voor een regelmatige polygoon is 1/2 keer het apothem vermenigvuldigd met de omtrek. De omtrek is slechts de lengte van één zijde vermenigvuldigd met het aantal zijden (n); voor een gewone polygoon, n vertegenwoordigt ook het aantal driehoeken waaruit de figuur bestaat. De formule is dan niets meer dan het gebied van een driehoek vermenigvuldigd met het aantal driehoeken in de veelhoek.[4]
3 Zie de overeenkomsten. Nogmaals, de formule voor een regelmatige polygoon is 1/2 keer het apothem vermenigvuldigd met de omtrek. De omtrek is slechts de lengte van één zijde vermenigvuldigd met het aantal zijden (n); voor een gewone polygoon, n vertegenwoordigt ook het aantal driehoeken waaruit de figuur bestaat. De formule is dan niets meer dan het gebied van een driehoek vermenigvuldigd met het aantal driehoeken in de veelhoek.[4]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bereken de omtrek. De omtrek is de gecombineerde lengte van de omtrek van een tweedimensionaal figuur. Voor een regelmatige polygoon kan deze worden berekend door de lengte van één zijde te vermenigvuldigen met het aantal zijden (n).[1]
1 Bereken de omtrek. De omtrek is de gecombineerde lengte van de omtrek van een tweedimensionaal figuur. Voor een regelmatige polygoon kan deze worden berekend door de lengte van één zijde te vermenigvuldigen met het aantal zijden (n).[1]  2 Bepaal de apothem. De afstand van een regelmatige veelhoek is de kortste afstand van het middelpunt tot één van de zijden, waardoor een rechte hoek ontstaat. Dit is een beetje lastiger om te berekenen dan de omtrek.
2 Bepaal de apothem. De afstand van een regelmatige veelhoek is de kortste afstand van het middelpunt tot één van de zijden, waardoor een rechte hoek ontstaat. Dit is een beetje lastiger om te berekenen dan de omtrek. 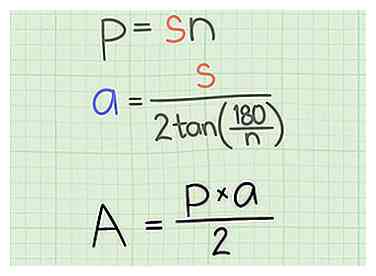 3 Ken de juiste formule. Het gebied van elke regelmatige veelhoek wordt gegeven door de formule: Gebied = (een X p)/2, waar een is de lengte van de apothem en p is de omtrek van de veelhoek.
3 Ken de juiste formule. Het gebied van elke regelmatige veelhoek wordt gegeven door de formule: Gebied = (een X p)/2, waar een is de lengte van de apothem en p is de omtrek van de veelhoek.  4 Sluit de waarden van een en p in de formule en haal het gebied op. Laten we als voorbeeld een zeskant (6 zijden) gebruiken met een zijde (s) lengte van 10.
4 Sluit de waarden van een en p in de formule en haal het gebied op. Laten we als voorbeeld een zeskant (6 zijden) gebruiken met een zijde (s) lengte van 10.  1 Begrijp dat een regelmatige polygoon kan worden beschouwd als een verzameling driehoeken. Elke zijde vertegenwoordigt de basis van een driehoek en er zijn evenveel driehoeken in de veelhoek als er zijden zijn. Elk van de driehoeken is gelijk in basislengte, hoogte en oppervlakte.[2]
1 Begrijp dat een regelmatige polygoon kan worden beschouwd als een verzameling driehoeken. Elke zijde vertegenwoordigt de basis van een driehoek en er zijn evenveel driehoeken in de veelhoek als er zijden zijn. Elk van de driehoeken is gelijk in basislengte, hoogte en oppervlakte.[2]  2 Denk aan de formule voor het gebied van een driehoek. Het gebied van een willekeurige driehoek is 1/2 keer de lengte van de basis (die in de veelhoek de lengte van een zijde is) vermenigvuldigd met de hoogte (die hetzelfde is als de apotheker in regelmatige veelhoek).[3]
2 Denk aan de formule voor het gebied van een driehoek. Het gebied van een willekeurige driehoek is 1/2 keer de lengte van de basis (die in de veelhoek de lengte van een zijde is) vermenigvuldigd met de hoogte (die hetzelfde is als de apotheker in regelmatige veelhoek).[3]  3 Zie de overeenkomsten. Nogmaals, de formule voor een regelmatige polygoon is 1/2 keer het apothem vermenigvuldigd met de omtrek. De omtrek is slechts de lengte van één zijde vermenigvuldigd met het aantal zijden (n); voor een gewone polygoon, n vertegenwoordigt ook het aantal driehoeken waaruit de figuur bestaat. De formule is dan niets meer dan het gebied van een driehoek vermenigvuldigd met het aantal driehoeken in de veelhoek.[4]
3 Zie de overeenkomsten. Nogmaals, de formule voor een regelmatige polygoon is 1/2 keer het apothem vermenigvuldigd met de omtrek. De omtrek is slechts de lengte van één zijde vermenigvuldigd met het aantal zijden (n); voor een gewone polygoon, n vertegenwoordigt ook het aantal driehoeken waaruit de figuur bestaat. De formule is dan niets meer dan het gebied van een driehoek vermenigvuldigd met het aantal driehoeken in de veelhoek.[4]