Hoe het gebied van een vierkant te vinden met behulp van de lengte van zijn diagonaal

De meest voorkomende formule voor het gebied van een vierkant is eenvoudig: het is de lengte van de vierkantkant, of s². Maar soms ken je alleen de lengte van de diagonaal van het vierkant, die tussen tegenoverliggende hoekpunten loopt. Als je de juiste driehoeken hebt bestudeerd, kun je een nieuwe gebiedsformule vinden die deze diagonaal als enige variabele gebruikt.

Deel een van de twee:
Het gebied vinden vanaf de diagonaal

1. 1 Teken je vierkant. Een vierkant heeft vier gelijke zijden. Laten we zeggen dat elk een lengte van "s" heeft.
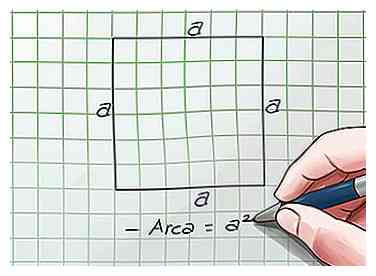2. 2 Bekijk de basisformule voor het gebied van een vierkant. Het gebied van een vierkant is gelijk aan de lengte in de breedte. Omdat elke kant is s, de formule is Gebied = s x s = s². Dit zal later nuttig zijn.
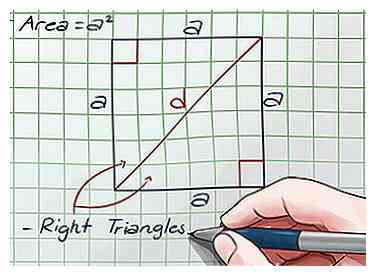3. 3 Verbind twee tegenover elkaar liggende hoeken om een ​​diagonaal te maken. Laat de maat van deze diagonaal zijn d units. Deze diagonaal verdeelt het vierkant in twee rechthoekige driehoeken.
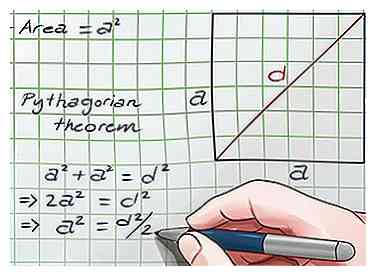4. 4 De stelling van Pythagoras toepassen op een van de driehoeken. De stelling van Pythagoras is een formule voor het vinden van de hypotenusa (langste zijde) van een rechthoekige driehoek: (zijkant)² + (zijde twee)² = (hypotenusa)²of $\ displaystyle a ^ 2 + b ^ 2 = c ^ 2$. Nu het vierkant in tweeën is verdeeld, kunt u deze formule gebruiken op een van de juiste driehoeken:
   • De twee kortere zijden van de driehoek zijn de zijkanten van het vierkant: elk heeft een lengte van s.
   • De hypotenusa is de diagonaal van het plein, d.
   • $\ displaystyle s ^ 2 + s ^ 2 = d ^ 2$
5. 5 Rangschik de vergelijking zo² staat aan de kant. Vergeet niet dat we al weten dat het gebied van het vierkant gelijk is aan s². Als je s kunt krijgen² alleen aan de zijkant, heb je een nieuwe vergelijking voor het gebied:
   • $\ displaystyle s ^ 2 + s ^ 2 = d ^ 2$
   • Makkelijker maken: $\ displaystyle 2s ^ 2 = d ^ 2$
   • Verdeel beide zijden door twee: $\ displaystyle s ^ 2 = \ frac d ^ 2 2$
   • Gebied = $\ displaystyle s ^ 2 = \ frac d ^ 2 2$
   • Gebied = $\ displaystyle \ frac d ^ 2 2$
6. 6 Gebruik deze formule op een voorbeeldvierkant. Deze stappen hebben bewezen dat de formule Area = $\ displaystyle \ frac d ^ 2 2$ werkt voor alle vierkanten. Sluit gewoon de lengte van de diagonaal in d en oplossen.
   • Laten we bijvoorbeeld zeggen dat een vierkant een diagonaal heeft van 10 cm.
   • Gebied = $\ displaystyle \ frac 10 ^ 2 2$
     = $\ displaystyle \ frac 100 2$
     = 50 vierkante centimeter.

Deel twee van twee:
Extra informatie

1. 1 Zoek de diagonaal uit de lengte van een zijkant. De stelling van Pythagoras voor een vierkant met zijde s en diagonaal d geeft je de formule $\ displaystyle 2s ^ 2 = d ^ 2$. Los op voor d als u de lengte van de zijkanten kent en de lengte van de diagonaal wilt weten:
   • $\ displaystyle 2s ^ 2 = d ^ 2$
     $\ displaystyle \ sqrt 2s ^ 2 = \ sqrt d ^ 2$
     $\ displaystyle s \ sqrt 2 = d$
   • Als een vierkant bijvoorbeeld zijden van 7 inch heeft, is de diagonaal d = 7√2 inch of ongeveer 9,9 inch.
   • Als u geen rekenmachine heeft, kunt u 1.4 gebruiken als schatting voor √2.
2. 2 Zoek de lengte van de zijkant van de diagonaal. Als je de diagonaal krijgt en je weet dat de diagonaal van een vierkant is $\ displaystyle s \ sqrt 2$, je kunt beide kanten opdelen $\ displaystyle \ sqrt 2$ krijgen $\ displaystyle s = \ frac d \ sqrt 2$.
   • Een vierkant met een diagonaal van 10 cm heeft bijvoorbeeld zijden met lengte $\ displaystyle \ frac 10 \ sqrt 2 = 7.071$ cm.
   • Als u zowel de lengte van de zijkant als het gebied van de diagonaal moet vinden, kunt u eerst deze formule gebruiken en vervolgens snel het antwoord verdelen om het gebied te krijgen: $\ displaystyle = s ^ 2 = 7.071 ^ 2 = 50$ vierkante centimeter. Dit is een beetje minder nauwkeurig, sindsdien $\ displaystyle \ sqrt 2$ is een irrationeel getal dat kan leiden tot afrondingsfouten.
3. 3 Interpreteer de gebiedsformule. De wiskunde zoekt naar de formule Area = $\ displaystyle \ frac d ^ 2 2$, maar is er een manier om dit direct te testen? Goed, $\ displaystyle d ^ 2$ is het gebied van een tweede vierkant met de diagonaal als een zijde. Omdat de volledige formule is $\ displaystyle \ frac d ^ 2 2$, je kunt redeneren dat dit tweede vierkant precies twee keer het gebied van het oorspronkelijke vierkant heeft. Je kunt dit zelf testen:
   • Teken een vierkant op een vel papier. Zorg ervoor dat alle zijden gelijk zijn.
   • Meet de diagonaal. Teken een tweede vierkant met die maat als de lengte van het vierkant.
   • Trek een kopie van je eerste vierkant, zodat je er twee hebt. Snijd alle drie de vierkanten eruit.
   • Knip de twee kleinere vierkanten in willekeurige vormen, zodat je ze in het grote vierkant kunt laten passen. Ze moeten de ruimte perfect vullen, en laten zien dat het gebied van het grotere vierkant precies twee keer zo groot is als het kleinere vierkant.