Hoe het gebied van een vierhoek te vinden (met cheat sheets)

Dus je hebt huiswerk gekregen dat vereist dat je het gebied van een vierhoek vindt ... maar je weet niet eens wat een vierhoek is. Maak je geen zorgen - hulp is hier! Een vierhoek is elke vorm met vier zijden - vierkanten, rechthoeken en ruiten zijn slechts enkele voorbeelden. Om het gebied van een vierhoek te vinden, hoeft u alleen maar het type vierhoek te identificeren waarmee u werkt en een eenvoudige formule te volgen. Dat is het!

Methode één van de vier:
Vierkanten, rechthoeken en andere parallellogrammen

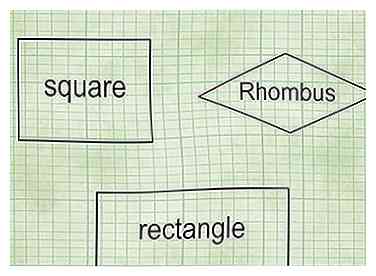1 Weet hoe je een parallellogram kunt identificeren. Een parallellogram is elke vierzijdige vorm met twee paren parallelle zijden waarbij de zijden tegenover elkaar dezelfde lengte hebben. Parallelogrammen omvatten:
- Squares: Vier zijden, allemaal even lang. Vier hoeken, alle 90 graden (rechte hoeken).
- rechthoeken: Vier zijden; tegenoverliggende zijden hebben dezelfde lengtes. Vier hoeken, alle 90 graden.
- ruiten: Vier zijden, allemaal met dezelfde lengte. Vier hoeken; geen enkele hoeft 90 graden te zijn, maar tegenovergestelde hoeken moeten dezelfde hoeken hebben.
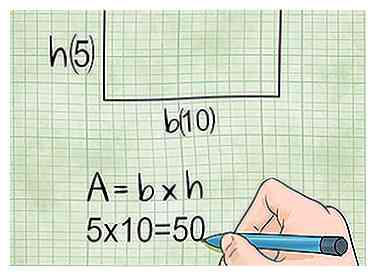2 Vermenigvuldig basistijden hoogte om het gebied van een rechthoek te krijgen. Om het gebied van een rechthoek te vinden, hebt u twee metingen nodig: de breedte of basis (de langere zijde van de rechthoek) en de lengte of hoogte (de kortere zijde van de rechthoek). Voeg ze vervolgens samen om het gebied te krijgen. Met andere woorden:
- Oppervlakte = basis × hoogteof A = b × h in het kort.
- Voorbeeld: Als de basis van een rechthoek een lengte van 10 inch heeft en de hoogte een lengte heeft van 5 inch, dan is het gebied van de rechthoek eenvoudigweg 10 × 5 (b x h) = 50 vierkante centimeter.
- Vergeet niet dat wanneer u het gebied van een vorm vindt, u het zult gebruiken vierkante eenheden (vierkante inch, vierkante voet, vierkante meter, etc.) voor uw antwoord.
3 Vermenigvuldig één kant apart om het gebied van een vierkant te vinden. Vierkanten zijn eigenlijk speciale rechthoeken, dus je kunt dezelfde formule gebruiken om hun gebied te vinden. Omdat de zijden van een vierkant allemaal even lang zijn, kunt u de snelkoppeling gebruiken door de lengte van een zijde alleen te vermenigvuldigen. Dit is hetzelfde als het vermenigvuldigen van de basis van het vierkant met zijn hoogte, omdat de basis en hoogte gewoon altijd hetzelfde zijn. Gebruik de volgende vergelijking:^[1]
- Gebied = zijde × zijkant of A = s²
- Voorbeeld: Als een zijde van een vierkant een lengte heeft van 4 voet (t = 4), dan is het gebied van dit vierkant eenvoudig t²of 4 x 4 = 16 vierkante voet.
4 Vermenigvuldig de diagonalen en deel ze door twee om het gebied van een ruit te vinden. Wees voorzichtig met deze - wanneer u het gebied van een ruit vindt, kunt u niet eenvoudig twee aangrenzende zijden vermenigvuldigen. Zoek in plaats daarvan de diagonalen (de lijnen die elke reeks tegenoverliggende hoeken verbinden), vermenigvuldig ze en deel ze door twee. Met andere woorden: ^[2]
- Oppervlakte = (Diag. 1 × Diag. 2) / 2 of A = (d₁ × d₂)/2
- Voorbeeld: Als een ruit diagonalen heeft met een lengte van 6 meter en 8 meter, dan is het gebied eenvoudig (6 × 8) / 2 = 48/2 = 24 vierkante meter.
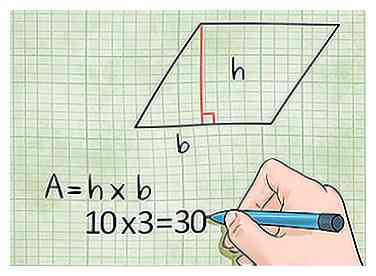5 U kunt ook de basis × hoogte gebruiken om het gebied van een ruit te vinden. Technisch gezien kun je ook de formule basistijdenhoogte gebruiken om het gebied van een ruit te vinden. Hier betekent "basis" en "hoogte" niet dat je alleen twee aangrenzende zijden kunt vermenigvuldigen. Kies eerst één kant om de basis te zijn. Teken vervolgens een lijn van de basis naar de andere kant. De lijn moet aan beide zijden op 90 graden liggen. De lengte van deze kant is wat je moet gebruiken voor de hoogte.
- Voorbeeld: Een ruit heeft zijden van 10 mijl en 5 mijl. De afstand in rechte lijn tussen de 16 km lange zijden is 3 mijl (4,8 km). Als u het gebied van de ruit wilt vinden, vermenigvuldigt u 10 × 3 = 30 vierkante mijlen.
6 Houd er rekening mee dat de formules ruit en rechthoek voor vierkanten werken. De bovenstaande zijgevel-formule voor vierkanten is veruit de handigste manier om het gebied voor deze vormen te vinden. Omdat vierkanten technisch zowel rechthoeken en ruiten als vierkanten zijn, kunt u de gebiedsformules van die vormen voor vierkanten gebruiken en het juiste antwoord krijgen. Met andere woorden, voor vierkanten:
- Oppervlakte = basis × hoogte of A = b × h
- Oppervlakte = (Diag. 1 × Diag. 2) / 2 of A = (d₁ × d₂)/2
- Voorbeeld: Een vierzijdige vorm heeft twee aangrenzende zijden met een lengte van 4 meter. Je kunt het gebied van dit vierkant vinden door de basistijden te vermenigvuldigen met de hoogte: 4 × 4 = 16 vierkante meter.
- Voorbeeld: De diagonalen van een vierkant zijn beide gelijk aan 10 centimeter. U kunt het gebied van dit vierkant vinden met de diagonale formule: (10 × 10) / 2 = 100/2 = 50 vierkante centimeter.

Methode twee van vier:
Het gebied van een trapezium vinden

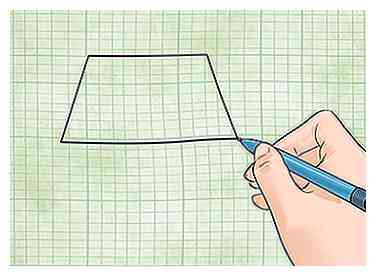1 Weet hoe je een trapezium kunt identificeren. Een trapezium is een vierhoek met ten minste twee zijden die parallel aan elkaar lopen. De hoeken kunnen willekeurige hoeken hebben. Elk van de vier zijden van een trapezium kan een andere lengte hebben.
- Er zijn twee verschillende manieren waarop je het gebied van een trapezium kunt vinden, afhankelijk van welke stukjes informatie je hebt. Hieronder ziet u hoe u beide kunt gebruiken.
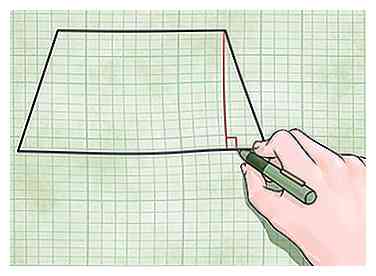2 Zoek de hoogte van de trapezium. De hoogte van een trapezoïde is de loodlijn die de twee evenwijdige zijden verbindt. Dit zal niet meestal dezelfde lengte als een van de zijkanten, omdat de zijkanten meestal diagonaal zijn gericht. Je hebt dit nodig voor beide gebiedsvergelijkingen. Zo kun je de hoogte van een trapezium vinden:^[3]
- Zoek de kortere van de twee basislijnen (de parallelle zijden). Plaats je potlood op de hoek tussen die basislijn en een van de niet-parallelle zijden.Teken een rechte lijn die haaks op de twee basislijnen ligt. Meet deze lijn om de hoogte te vinden.
- U kunt soms ook trigonometrie gebruiken om de hoogte te bepalen als de hoogtelijn, de basis en de andere zijde een rechthoekige driehoek vormen. Zie ons trig-artikel voor meer informatie.
3 Zoek het gebied van de trapezoïde op basis van de hoogte en de lengte van de basis. Als u de hoogte van de trapezoïde en de lengte van beide bases kent, gebruikt u de volgende vergelijking:
- Oppervlakte = (basis 1 + basis 2) / 2 × hoogte of A = (a + b) / 2 × h
- Voorbeeld: Als je een trapezium hebt met één basis van 7 yards, een andere basis van 11 yards, en de hoogtelijn die hen verbindt is 2 meter lang, kun je het gebied als volgt vinden: (7 + 11) / 2 × 2 = (18) / 2 × 2 = 9 × 2 = 18 vierkante meter.
- Als de hoogte 10 is en de basis de lengte heeft van 7 en 9, dan kun je het gebied eenvoudig vinden door het volgende te doen: (7 + 9) / 2 * 10 = (16/2) * 10 = 8 * 10 = 80
4 Vermenigvuldig het middensegment met twee om het gebied van een trapezium te vinden. Het middensegment is een denkbeeldige lijn die evenwijdig loopt aan de onderste en bovenste lijnen van de trapezium en op precies dezelfde afstand van elkaar ligt. Omdat de middensegment is altijd gelijk aan (Base 1 + Base 2) / 2, als u het weet, kunt u een snelkoppeling gebruiken voor de trapezoïde formule:
- Oppervlakte = middensegment × hoogte of A = m × h
- In wezen is dit hetzelfde als het gebruik van de oorspronkelijke formule, behalve dat u "m" gebruikt in plaats van (a + b) / 2.
- 'Voorbeeld:' Het middensegment van de trapezium in het bovenstaande voorbeeld is 9 meter lang. Dit betekent dat we het gebied van de trapezoïde eenvoudig kunnen vinden door 9 x 2 = te vermenigvuldigen 18 vierkante meter, Net als eerst.

Methode drie van vier:
Het gebied van een vlieger vinden

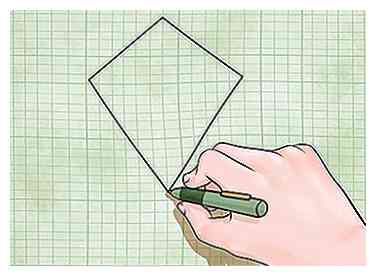1 Weet hoe je een vlieger moet identificeren. Een vlieger heeft een vierzijdige vorm met twee paar zijden van gelijke lengte aangrenzend naar elkaar, niet tegenover elkaar. Zoals hun naam doet vermoeden, lijken vliegers op echte vliegers.
- Er zijn twee verschillende manieren om het gebied van een vlieger te vinden, afhankelijk van welke stukjes informatie je hebt. Hieronder vindt u hoe u beide kunt gebruiken.
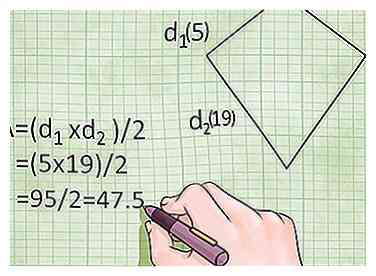2 Gebruik de rhombus diagonale formule om het gebied van een vlieger te vinden. Omdat een ruit gewoon een speciaal soort vlieger is waarvan de zijkanten even lang zijn, kun je de diagonale ruitformule ook gebruiken om een vliegergebied te vinden. Ter herinnering, diagonalen zijn de rechte lijnen tussen twee tegenovergestelde hoeken op de vlieger. Net als een ruit is de vliegeroppervlakformule:
- Oppervlakte = (Diag. 1 x Diag 2.) / 2 of A = (d₁ × d₂)/2
- Voorbeeld: Als een vlieger diagonalen heeft met een lengte van 19 meter en 5 meter, dan is het gebied eenvoudig (19 × 5) / 2 = 95/2 = 47.5 vierkante meter.
- Als u de lengte van de diagonalen niet weet en ze niet kunt meten, kunt u trigonometrie gebruiken om ze te berekenen. Zie ons artikel over het vinden van het gebied van een vlieger voor meer informatie.
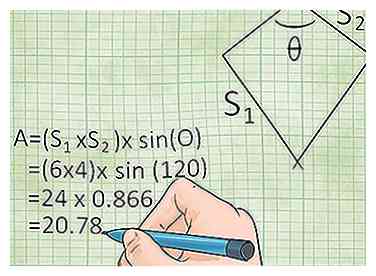3 Gebruik de lengtes van de zijden en de hoek ertussen om het gebied te vinden. Als je de twee verschillende waarden kent voor de lengtes van de zijkanten en de hoek in de hoek tussen die zijden, kun je het gebied van de vlieger oplossen met de principes van trigonometrie.^[4] Voor deze methode moet u weten hoe u sinusfuncties moet uitvoeren (of u moet op zijn minst een rekenmachine met een sinusfunctie hebben). Zie ons trig-artikel voor meer informatie of gebruik de onderstaande formule:
- Gebied = (zijde 1 × zijde 2) × sin (hoek) of A = (s₁ × s₂) × sin (θ) (waarbij θ de hoek tussen zijden 1 en 2 is).
- Voorbeeld: Je hebt een vlieger met twee zijden van lengte 6 voet en twee zijden van lengte 4 voet. De hoek ertussen is ongeveer 120 graden. In dit geval kunt u het gebied als volgt oplossen: (6 × 4) × sin (120) = 24 × 0.866 = 20,78 vierkante voet
- Merk op dat je de twee moet gebruiken verschillend zijden en de hoek hiertussen - het gebruik van de set zijden met dezelfde lengte zal niet werken.

Methode vier van vier:
Oplossen voor elke vierhoek

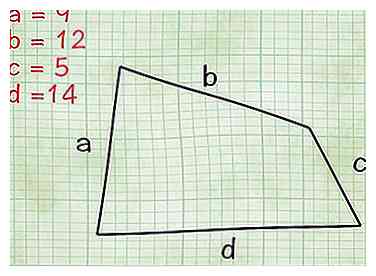1 Zoek de lengtes van alle vier de zijden. Valt uw vierhoek niet in een van de categorieën netjes opruimen (bijvoorbeeld, heeft deze zijden met alle verschillende lengtes en nul parallelle reeksen zijden?) Geloof het of niet, er zijn formules die u kunt gebruiken om het gebied van elke zijde te bepalen vierhoek, ongeacht de vorm. In deze sectie vindt u hoe u de meest gebruikelijke kunt gebruiken. Merk op dat deze formule kennis van trigonometrie vereist (nogmaals, hier is onze standaard trig-gids.
- Eerst moet je de lengtes van elk van de vier zijden van de vierhoek vinden. Voor de doeleinden van dit artikel zullen we ze labelen een, b, c en d. Sides een en c zijn tegenovergesteld aan elkaar en zijden b en d zijn tegenover elkaar.
- Voorbeeld: Als je een vreemd gevormde vierhoek hebt die niet in een van de bovenstaande categorieën past, meet dan eerst de vier zijden. Laten we zeggen dat ze lengtes hebben van 12, 9, 5 en 14 inch. In de onderstaande stappen gebruikt u deze informatie om het gebied van de vorm te vinden.
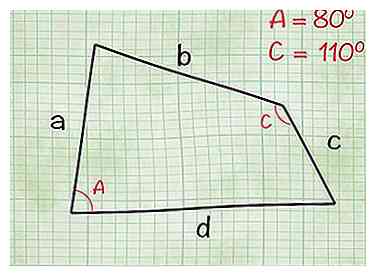2 Zoek de hoeken tussen een en d en b en c. Wanneer u met een onregelmatige vierhoek werkt, kunt u het gebied niet alleen aan de zijkanten vinden. Ga verder door twee van de tegenovergestelde hoeken te vinden. Voor de doeleinden van deze sectie gebruiken we hoek EEN tussen kanten een en den hoek C tussen kanten b en c. U kunt dit echter ook doen met de twee andere tegenovergestelde hoeken.
- Voorbeeld: Laten we zeggen dat in je vierhoek, EEN is gelijk aan 80 graden en C is gelijk aan 110 graden. In de volgende stap gebruikt u deze waarden om het totale gebied te vinden.
3 Gebruik de driehoeksgebiedformule om het gebied van de vierhoek te vinden. Stel je voor dat er een rechte lijn is vanuit de hoek ertussen een en b naar de hoek tussen c en d. Deze lijn verdeelt de vierhoek in twee driehoeken. Omdat het gebied van een driehoek is abzondeC, waar C is de hoek tussen zijden een en b, je kunt deze formule twee keer gebruiken (een keer voor elk van je denkbeeldige driehoeken) om het totale gebied van de vierhoek te krijgen. Met andere woorden, voor elke vierhoek:
- Oppervlakte = 0,5 Zij 1 × Zij 4 × sin (Zij 1 & 4 hoek) + 0,5 × Zij 2 × Zij 3 × sin (Zij 2 & 3 hoek) of
- Oppervlakte = 0,5 a × d × sin A + 0,5 × b × c × sin C
- Voorbeeld: Je hebt al de zijkanten en hoeken die je nodig hebt, dus laten we het oplossen:
  
  = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
  
  = 84 × sin (80) + 22.5 × sin (110)
  
  = 84 × 0.984 + 22.5 × 0.939
  
  = 82.66 + 21.13 = 103,79 vierkante inch
- Merk op dat als u het gebied van een parallellogram probeert te vinden, waarin de tegenovergestelde hoeken gelijk zijn, de vergelijking vermindert tot Oppervlakte = 0,5 * (ad + bc) * sin A.