Een prisma is een driedimensionale vorm met twee parallelle, congruente basen.[1] In een driehoekig prisma zijn de basissen driehoeken. Een driehoekig prisma heeft ook drie zijkanten. Om het oppervlak van het driehoekige prisma te vinden, moet je eerst het gebied van de zijkanten vinden, daarna moet je het gebied van de basis vinden. Ten slotte moet u deze twee gebieden bij elkaar optellen om de totale oppervlakte te vinden. Deze stappen worden weergegeven door de formule , waar is gelijk aan het laterale gedeelte van het prisma en is gelijk aan het oppervlak van één basis.
Deel een van de drie:
Het zijgebied vinden
-
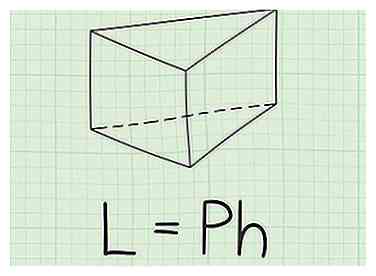 1 Schrijf de formule op voor het vinden van het laterale gebied van een driehoekig prisma. De formule is , waar is gelijk aan het laterale deel van het prisma, is gelijk aan de omtrek van één basis, en is gelijk aan de hoogte van het prisma.[2]
1 Schrijf de formule op voor het vinden van het laterale gebied van een driehoekig prisma. De formule is , waar is gelijk aan het laterale deel van het prisma, is gelijk aan de omtrek van één basis, en is gelijk aan de hoogte van het prisma.[2] - Het laterale gedeelte van een prisma is het oppervlak van alle zijden of gezichten, die niet de basis zijn.[3]
-
 2 Bereken de omtrek van één basis. De basis is een driehoek, dus het heeft drie zijden. Het gebied van de omtrek van een driehoek is , waar , , en zijn de lengte van elke zijde van de driehoek.[4] Het maakt niet uit welke basis je gebruikt om te berekenen, omdat de twee bases van een prisma congruent zijn.[5]
2 Bereken de omtrek van één basis. De basis is een driehoek, dus het heeft drie zijden. Het gebied van de omtrek van een driehoek is , waar , , en zijn de lengte van elke zijde van de driehoek.[4] Het maakt niet uit welke basis je gebruikt om te berekenen, omdat de twee bases van een prisma congruent zijn.[5] - Als de basis bijvoorbeeld drie zijden heeft van 6 cm, 5 cm en 4 cm, om de omtrek te berekenen, telt u alle drie de zijden op: . De omtrek van één basis is dus 15 cm.
-
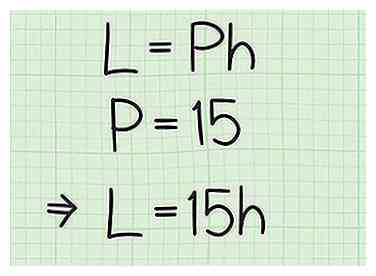 3 Sluit de omtrek aan op de formule voor het zijoppervlak. Zorg ervoor dat je de variabele vervangt in de formule.
3 Sluit de omtrek aan op de formule voor het zijoppervlak. Zorg ervoor dat je de variabele vervangt in de formule. - Bijvoorbeeld, .
-
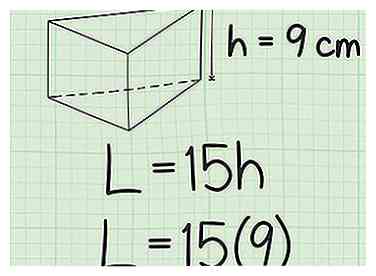 4 Steek de hoogte van het prisma in de laterale gebiedsformule. De hoogte van het prisma is hetzelfde als de lengte van de zijkant van een zijvlak dat niet is verbonden met de basis. Meestal (maar niet altijd) is dit de langere zijde van het zijvlak.
4 Steek de hoogte van het prisma in de laterale gebiedsformule. De hoogte van het prisma is hetzelfde als de lengte van de zijkant van een zijvlak dat niet is verbonden met de basis. Meestal (maar niet altijd) is dit de langere zijde van het zijvlak. - Als de hoogte van het prisma bijvoorbeeld 9 cm is, ziet uw formule er als volgt uit: .
-
 5 Vermenigvuldig de omtrek van een basis met de hoogte van het prisma. Het resultaat geeft u in vierkante eenheden het laterale oppervlak van het prisma. Dit is de eerste waarde die u nodig hebt om het totale oppervlak van het prisma te vinden, dus zet deze waarde opzij terwijl u het gebied van de basis berekent.
5 Vermenigvuldig de omtrek van een basis met de hoogte van het prisma. Het resultaat geeft u in vierkante eenheden het laterale oppervlak van het prisma. Dit is de eerste waarde die u nodig hebt om het totale oppervlak van het prisma te vinden, dus zet deze waarde opzij terwijl u het gebied van de basis berekent. - Bijvoorbeeld, Dus, het zijoppervlak van het prisma is 135 vierkante centimeter.
Tweede deel van de drie:
Het gebied van de basis vinden
-
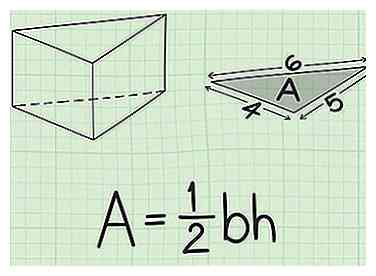 1 Stel de formule in voor het gebied van een driehoek. Omdat de basis van een driehoekig prisma driehoeken zijn, gebruikt u deze formule om hun gebied te berekenen. De formule voor het gebied van een driehoek is , waar is gelijk aan het gebied van de driehoek, is gelijk aan de basis van de driehoek, en is gelijk aan de hoogte van de driehoek.[6]
1 Stel de formule in voor het gebied van een driehoek. Omdat de basis van een driehoekig prisma driehoeken zijn, gebruikt u deze formule om hun gebied te berekenen. De formule voor het gebied van een driehoek is , waar is gelijk aan het gebied van de driehoek, is gelijk aan de basis van de driehoek, en is gelijk aan de hoogte van de driehoek.[6] - Dit is de meest gebruikelijke manier om het gebied van een driehoek te berekenen. Als u de hoogte van de driehoek niet weet, kunt u het gebied ook berekenen aan de hand van de lengte van de drie zijden van de driehoek.
- Je hoeft maar het gebied van één basis te vinden, omdat de twee bases van een prisma congruent zijn en daarom hetzelfde gebied hebben.[7]
-
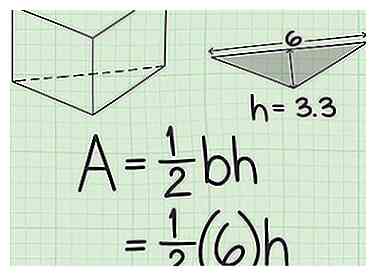 2 Steek de basis van de driehoek in de formule. Verwar de basis niet met een andere kant van de driehoek. De basis is de zijkant loodrecht op de hoogte.
2 Steek de basis van de driehoek in de formule. Verwar de basis niet met een andere kant van de driehoek. De basis is de zijkant loodrecht op de hoogte. - Als de basis van de driehoek bijvoorbeeld 6 cm is, ziet uw formule er als volgt uit: .
-
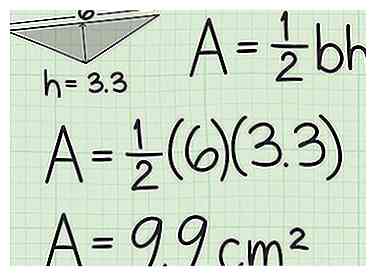 3 Steek de hoogte van de driehoek in de formule. Vermenigvuldig de basis met de hoogte. Neem dan de helft van deze waarde. Dit geeft je het gebied van de basis, in vierkante eenheden. Dit is de tweede waarde die u nodig hebt om het totale oppervlak van het prisma te berekenen.
3 Steek de hoogte van de driehoek in de formule. Vermenigvuldig de basis met de hoogte. Neem dan de helft van deze waarde. Dit geeft je het gebied van de basis, in vierkante eenheden. Dit is de tweede waarde die u nodig hebt om het totale oppervlak van het prisma te berekenen. - Als de hoogte bijvoorbeeld 3,3 cm is, zien uw berekeningen er als volgt uit:
Het oppervlak van de basis is dus 9,9 vierkante centimeter.
- Als de hoogte bijvoorbeeld 3,3 cm is, zien uw berekeningen er als volgt uit:
Derde deel van de drie:
Het oppervlak vinden
-
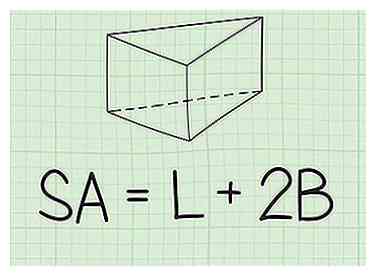 1 Stel de formule in om het oppervlak van een prisma te vinden. De formule is , waar is gelijk aan het oppervlak van het prisma, is gelijk aan het laterale gedeelte van het prisma, en is gelijk aan het oppervlak van één basis.[8]
1 Stel de formule in om het oppervlak van een prisma te vinden. De formule is , waar is gelijk aan het oppervlak van het prisma, is gelijk aan het laterale gedeelte van het prisma, en is gelijk aan het oppervlak van één basis.[8] -
 2 Steek het zijgedeelte in de formule. Dit is het oppervlak van alle zijden van het prisma die niet de basis vormen. Je had dit eerder moeten berekenen. Zorg ervoor dat u het laterale gebied vervangt door de variabele .
2 Steek het zijgedeelte in de formule. Dit is het oppervlak van alle zijden van het prisma die niet de basis vormen. Je had dit eerder moeten berekenen. Zorg ervoor dat u het laterale gebied vervangt door de variabele . - Als het zijgebied van uw driehoekige prisma bijvoorbeeld 135 vierkante centimeter is, ziet uw formule er als volgt uit: .
-
 3 Steek het gebied van één basis in de formule. Zorg ervoor dat je het gebied van slechts één basis gebruikt, niet het totale gebied van beide basen gecombineerd. Vervang het basisgebied voor de variabele .
3 Steek het gebied van één basis in de formule. Zorg ervoor dat je het gebied van slechts één basis gebruikt, niet het totale gebied van beide basen gecombineerd. Vervang het basisgebied voor de variabele . - Als het gebied van één basis van uw prisma bijvoorbeeld 9,9 vierkante centimeter is, ziet uw formule er als volgt uit: .
-
 4 Voer de berekeningen uit. Vermenigvuldig het gebied van de basis met 2 en voeg vervolgens het laterale gebied toe. Dit geeft je de totale oppervlakte, in vierkante eenheden, van je driehoekige prisma.
4 Voer de berekeningen uit. Vermenigvuldig het gebied van de basis met 2 en voeg vervolgens het laterale gebied toe. Dit geeft je de totale oppervlakte, in vierkante eenheden, van je driehoekige prisma. - Bijvoorbeeld:
Dus heeft het oppervlak van een driehoekig prisma met een basis met zijden van 6, 5 en 4 centimeter lang en een hoogte van 9 centimeter lang een oppervlak van 154,8 vierkante centimeter.
- Bijvoorbeeld:
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Schrijf de formule op voor het vinden van het laterale gebied van een driehoekig prisma. De formule is
1 Schrijf de formule op voor het vinden van het laterale gebied van een driehoekig prisma. De formule is  2 Bereken de omtrek van één basis. De basis is een driehoek, dus het heeft drie zijden. Het gebied van de omtrek van een driehoek is
2 Bereken de omtrek van één basis. De basis is een driehoek, dus het heeft drie zijden. Het gebied van de omtrek van een driehoek is  3 Sluit de omtrek aan op de formule voor het zijoppervlak. Zorg ervoor dat je de variabele vervangt
3 Sluit de omtrek aan op de formule voor het zijoppervlak. Zorg ervoor dat je de variabele vervangt  4 Steek de hoogte van het prisma in de laterale gebiedsformule. De hoogte van het prisma is hetzelfde als de lengte van de zijkant van een zijvlak dat niet is verbonden met de basis. Meestal (maar niet altijd) is dit de langere zijde van het zijvlak.
4 Steek de hoogte van het prisma in de laterale gebiedsformule. De hoogte van het prisma is hetzelfde als de lengte van de zijkant van een zijvlak dat niet is verbonden met de basis. Meestal (maar niet altijd) is dit de langere zijde van het zijvlak.  5 Vermenigvuldig de omtrek van een basis met de hoogte van het prisma. Het resultaat geeft u in vierkante eenheden het laterale oppervlak van het prisma. Dit is de eerste waarde die u nodig hebt om het totale oppervlak van het prisma te vinden, dus zet deze waarde opzij terwijl u het gebied van de basis berekent.
5 Vermenigvuldig de omtrek van een basis met de hoogte van het prisma. Het resultaat geeft u in vierkante eenheden het laterale oppervlak van het prisma. Dit is de eerste waarde die u nodig hebt om het totale oppervlak van het prisma te vinden, dus zet deze waarde opzij terwijl u het gebied van de basis berekent.  1 Stel de formule in voor het gebied van een driehoek. Omdat de basis van een driehoekig prisma driehoeken zijn, gebruikt u deze formule om hun gebied te berekenen. De formule voor het gebied van een driehoek is
1 Stel de formule in voor het gebied van een driehoek. Omdat de basis van een driehoekig prisma driehoeken zijn, gebruikt u deze formule om hun gebied te berekenen. De formule voor het gebied van een driehoek is  2 Steek de basis van de driehoek in de formule. Verwar de basis niet met een andere kant van de driehoek. De basis is de zijkant loodrecht op de hoogte.
2 Steek de basis van de driehoek in de formule. Verwar de basis niet met een andere kant van de driehoek. De basis is de zijkant loodrecht op de hoogte. 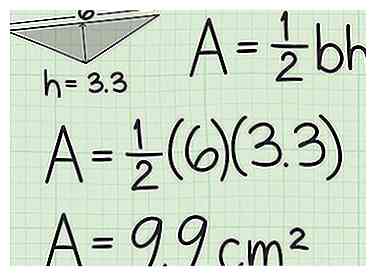 3 Steek de hoogte van de driehoek in de formule. Vermenigvuldig de basis met de hoogte. Neem dan de helft van deze waarde. Dit geeft je het gebied van de basis, in vierkante eenheden. Dit is de tweede waarde die u nodig hebt om het totale oppervlak van het prisma te berekenen.
3 Steek de hoogte van de driehoek in de formule. Vermenigvuldig de basis met de hoogte. Neem dan de helft van deze waarde. Dit geeft je het gebied van de basis, in vierkante eenheden. Dit is de tweede waarde die u nodig hebt om het totale oppervlak van het prisma te berekenen.  1 Stel de formule in om het oppervlak van een prisma te vinden. De formule is
1 Stel de formule in om het oppervlak van een prisma te vinden. De formule is  2 Steek het zijgedeelte in de formule. Dit is het oppervlak van alle zijden van het prisma die niet de basis vormen. Je had dit eerder moeten berekenen. Zorg ervoor dat u het laterale gebied vervangt door de variabele
2 Steek het zijgedeelte in de formule. Dit is het oppervlak van alle zijden van het prisma die niet de basis vormen. Je had dit eerder moeten berekenen. Zorg ervoor dat u het laterale gebied vervangt door de variabele  3 Steek het gebied van één basis in de formule. Zorg ervoor dat je het gebied van slechts één basis gebruikt, niet het totale gebied van beide basen gecombineerd. Vervang het basisgebied voor de variabele
3 Steek het gebied van één basis in de formule. Zorg ervoor dat je het gebied van slechts één basis gebruikt, niet het totale gebied van beide basen gecombineerd. Vervang het basisgebied voor de variabele  4 Voer de berekeningen uit. Vermenigvuldig het gebied van de basis met 2 en voeg vervolgens het laterale gebied toe. Dit geeft je de totale oppervlakte, in vierkante eenheden, van je driehoekige prisma.
4 Voer de berekeningen uit. Vermenigvuldig het gebied van de basis met 2 en voeg vervolgens het laterale gebied toe. Dit geeft je de totale oppervlakte, in vierkante eenheden, van je driehoekige prisma.