Er zijn verschillende manieren om een ontbrekende dimensie van een rechthoek te vinden en de methode die u gebruikt, is afhankelijk van welke informatie u al hebt. Zolang u het gebied of de omtrek kent, evenals de lengte van een zijde van de rechthoek (of de relatie tussen de lengte en breedte), kunt u een ontbrekende dimensie vinden. De eigenschappen van een rechthoek zijn zodanig dat u deze methoden kunt gebruiken om de breedte of lengte te vinden.
Methode één van de vier:
Gebied en lengte gebruiken
-
 1 Stel de formule in voor het gebied van een rechthoek. De formule is , waar is gelijk aan het gebied van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[1]
1 Stel de formule in voor het gebied van een rechthoek. De formule is , waar is gelijk aan het gebied van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[1] - Deze methode werkt alleen als u het gebied en de lengte van de rechthoek hebt opgegeven.
- U ziet mogelijk ook de formule die is geschreven als , waar is gelijk aan de hoogte van de rechthoek en wordt gebruikt in plaats van de lengte.[2] Deze twee termen verwijzen naar dezelfde meting.
-
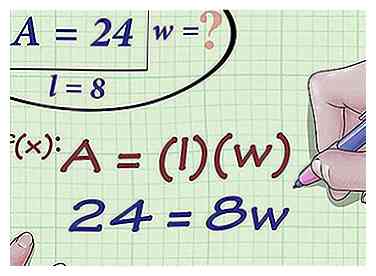 2 Steek de waarden voor het gebied en de lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor het gebied en de lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt. - Als u bijvoorbeeld de breedte van een rechthoek met een oppervlakte van 24 vierkante centimeter en een lengte van 8 centimeter probeert te vinden, ziet uw formule er als volgt uit:
- Als u bijvoorbeeld de breedte van een rechthoek met een oppervlakte van 24 vierkante centimeter en een lengte van 8 centimeter probeert te vinden, ziet uw formule er als volgt uit:
-
 3 Oplossen voor . Om dit te doen, moet u elke zijde van de vergelijking verdelen over de lengte.
3 Oplossen voor . Om dit te doen, moet u elke zijde van de vergelijking verdelen over de lengte. - Bijvoorbeeld in de vergelijking , zou je elke kant delen door 8.
- Bijvoorbeeld in de vergelijking , zou je elke kant delen door 8.
-
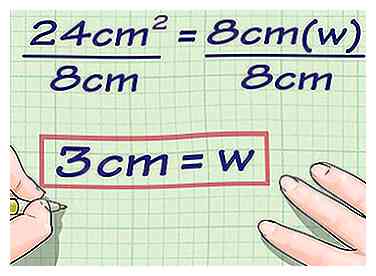 4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen. - Bijvoorbeeld voor een rechthoek met een gebied van en een lengte van zou de breedte zijn .
Methode twee van vier:
Omtrek en lengte gebruiken
-
 1 Stel de formule in voor de omtrek van een rechthoek. De formule is , waar is gelijk aan de omtrek van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[3]
1 Stel de formule in voor de omtrek van een rechthoek. De formule is , waar is gelijk aan de omtrek van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[3] - Deze methode werkt alleen als u de omtrek en lengte van de rechthoek hebt gekregen.
- U ziet mogelijk ook de formule die is geschreven als , waar is gelijk aan de hoogte van de rechthoek en wordt gebruikt in plaats van de lengte.[4] De variabelen en verwijzen naar dezelfde meting, en de distributieve eigenschap dicteert dat deze twee formules, hoewel anders gerangschikt, u hetzelfde resultaat zullen geven.
-
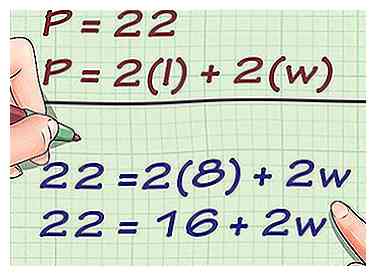 2 Steek de waarden voor omtrek en lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor omtrek en lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt. - Als u bijvoorbeeld de breedte van een rechthoek met een omtrek van 22 centimeter en een lengte van 8 centimeter probeert te vinden, ziet uw formule er als volgt uit:
- Als u bijvoorbeeld de breedte van een rechthoek met een omtrek van 22 centimeter en een lengte van 8 centimeter probeert te vinden, ziet uw formule er als volgt uit:
-
 3 Oplossen voor . Om dit te doen, moet u de lengte van elke kant van de vergelijking aftrekken en vervolgens delen door 2.
3 Oplossen voor . Om dit te doen, moet u de lengte van elke kant van de vergelijking aftrekken en vervolgens delen door 2. - Bijvoorbeeld in de vergelijking , je zou 16 van elke kant aftrekken, en dan delen door 2.
- Bijvoorbeeld in de vergelijking , je zou 16 van elke kant aftrekken, en dan delen door 2.
-
 4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen. - Bijvoorbeeld voor een rechthoek met een omtrek van en een lengte van zou de breedte zijn .
Methode drie van vier:
De diagonaal en lengte gebruiken
-
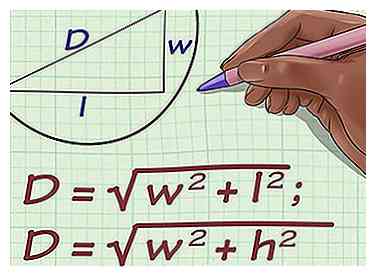 1 Stel de formule in voor de diagonaal van een rechthoek. De formule is , waar is gelijk aan de lengte van de diagonaal van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[5]
1 Stel de formule in voor de diagonaal van een rechthoek. De formule is , waar is gelijk aan de lengte van de diagonaal van de rechthoek, is gelijk aan de lengte van de rechthoek, en is gelijk aan de breedte van de rechthoek.[5] - Deze methode werkt alleen als u de lengte van de diagonaal en de lengte van de zijkant van de rechthoek hebt opgegeven.
- U ziet mogelijk ook de formule die is geschreven als , waar is gelijk aan de hoogte van de rechthoek en wordt gebruikt in plaats van de lengte.[6] De variabelen en refereer naar dezelfde meting.
-
 2 Steek de waarden voor de diagonaal en de lengte van de zijkant in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor de diagonaal en de lengte van de zijkant in de formule. Zorg ervoor dat u de juiste variabelen vervangt. - Als u bijvoorbeeld de breedte van een rechthoek met een diagonale lengte van 5 centimeter en een lengte van 4 centimeter aan de zijkant probeert te vinden, ziet uw formule er als volgt uit:
-
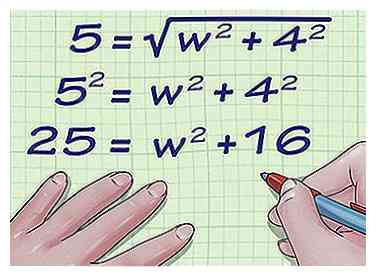 3 Vierkant van beide zijden van de formule. U moet dit doen om van het vierkantswortelbord af te komen, wat het isoleren van de breedtevariabele eenvoudiger maakt.
3 Vierkant van beide zijden van de formule. U moet dit doen om van het vierkantswortelbord af te komen, wat het isoleren van de breedtevariabele eenvoudiger maakt. - Bijvoorbeeld:
- Bijvoorbeeld:
-
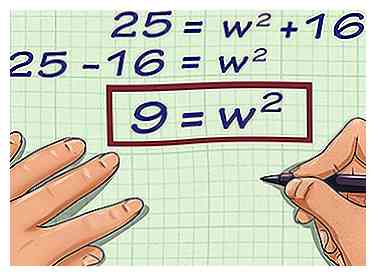 4 Isoleer de variabel. Om dit te doen, moet u de vierkante lengte van elke kant van de vergelijking aftrekken.
4 Isoleer de variabel. Om dit te doen, moet u de vierkante lengte van elke kant van de vergelijking aftrekken. - Bijvoorbeeld in de vergelijking , je zou 16 van elke kant aftrekken.
- Bijvoorbeeld in de vergelijking , je zou 16 van elke kant aftrekken.
-
 5 Oplossen voor . Om dit te doen, moet je de vierkantswortel van elke kant van de vergelijking vinden.
5 Oplossen voor . Om dit te doen, moet je de vierkantswortel van elke kant van de vergelijking vinden. - Bijvoorbeeld:
- Bijvoorbeeld:
-
 6 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
6 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen. - Bijvoorbeeld voor een rechthoek met een diagonale lengte van en een lengte van de zijkant van zou de breedte zijn .
Methode vier van vier:
Gebied of perimeter en relatieve lengte gebruiken
-
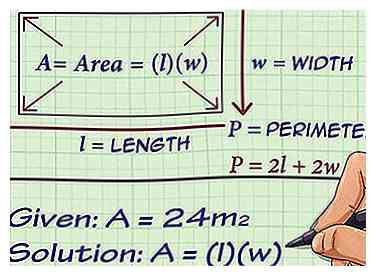 1 Stel de formule in voor het gebied of de omtrek van een rechthoek. Welke formule u gebruikt, hangt af van de meting die u krijgt. Als u het gebied krijgt, stelt u de gebiedformule in. Als u de perimeter krijgt, stelt u de perimeterformule in.
1 Stel de formule in voor het gebied of de omtrek van een rechthoek. Welke formule u gebruikt, hangt af van de meting die u krijgt. Als u het gebied krijgt, stelt u de gebiedformule in. Als u de perimeter krijgt, stelt u de perimeterformule in. - Als u het gebied of de perimeter niet kent, of de relatie tussen de lengte en de breedte, kunt u deze methode niet gebruiken.
- De formule voor gebied is .
- De formule voor de perimeter is .
- U weet bijvoorbeeld dat het gebied van een rechthoek 24 vierkante centimeter is, dus u zou de formule voor het gebied van een rechthoek instellen.
-
 2 Schrijf de uitdrukking die de relatie tussen de lengte en de breedte beschrijft. Schrijf je expressie in termen van wat gelijken.
2 Schrijf de uitdrukking die de relatie tussen de lengte en de breedte beschrijft. Schrijf je expressie in termen van wat gelijken. - De relatie kan worden gegeven door te zeggen hoeveel keer groter de ene kant is dan de andere, of hoeveel eenheden meer of minder is.
- U weet bijvoorbeeld dat de lengte vijf centimeter langer is dan de breedte. Je uitdrukking voor de lengte is dan .
-
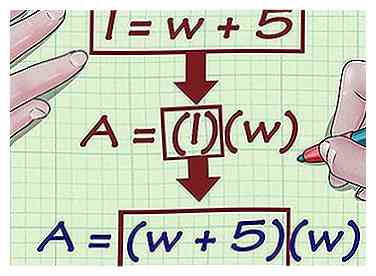 3 Vervang de variabele in uw gebied (of perimeter) formule met de uitdrukking voor lengte. Uw formule zou nu alleen de variabele moeten bevatten , wat betekent dat je de breedte kunt oplossen.
3 Vervang de variabele in uw gebied (of perimeter) formule met de uitdrukking voor lengte. Uw formule zou nu alleen de variabele moeten bevatten , wat betekent dat je de breedte kunt oplossen. - Bijvoorbeeld, als u weet dat dat gebied 24 vierkante centimeter is, en dat , je formule ziet er als volgt uit:
- Bijvoorbeeld, als u weet dat dat gebied 24 vierkante centimeter is, en dat , je formule ziet er als volgt uit:
-
 4 Vereenvoudig de vergelijking. Uw vereenvoudigde vergelijking kan verschillende vormen aannemen, afhankelijk van de relatie tussen de lengte en de breedte en afhankelijk van of u met een gebied of perimeter werkt.[7] Denk aan het opstellen van een vergelijking waarmee je kunt oplossen op de eenvoudigste manier.
4 Vereenvoudig de vergelijking. Uw vereenvoudigde vergelijking kan verschillende vormen aannemen, afhankelijk van de relatie tussen de lengte en de breedte en afhankelijk van of u met een gebied of perimeter werkt.[7] Denk aan het opstellen van een vergelijking waarmee je kunt oplossen op de eenvoudigste manier. - U kunt bijvoorbeeld vereenvoudigen naar .
-
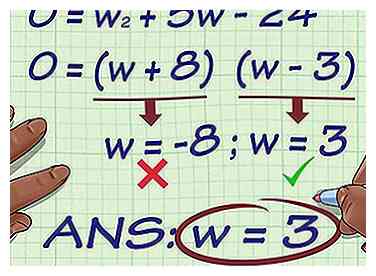 5 Oplossen voor . Nogmaals, hoe je het oplost zal afhangen van uw vereenvoudigde vergelijking. Gebruik de basisregels van algebra en geometrie om op te lossen.
5 Oplossen voor . Nogmaals, hoe je het oplost zal afhangen van uw vereenvoudigde vergelijking. Gebruik de basisregels van algebra en geometrie om op te lossen. - Mogelijk moet je optellen of delen gebruiken om op te lossen, of moet je een kwadratische vergelijking factoreren of de kwadratische formule gebruiken om op te lossen.[8]
- Bijvoorbeeld, kan als volgt worden verwerkt:
U hebt dan twee mogelijke oplossingen voor : of . Aangezien een rechthoek geen negatieve breedte kan hebben, kunt u -8 elimineren. Dus jouw oplossing is .[9]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Stel de formule in voor het gebied van een rechthoek. De formule is
1 Stel de formule in voor het gebied van een rechthoek. De formule is 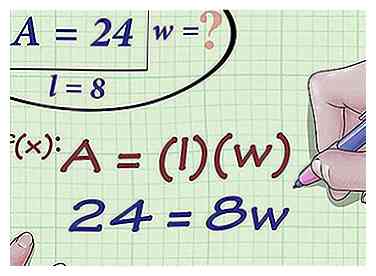 2 Steek de waarden voor het gebied en de lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor het gebied en de lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.  3 Oplossen voor
3 Oplossen voor  4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.  1 Stel de formule in voor de omtrek van een rechthoek. De formule is
1 Stel de formule in voor de omtrek van een rechthoek. De formule is 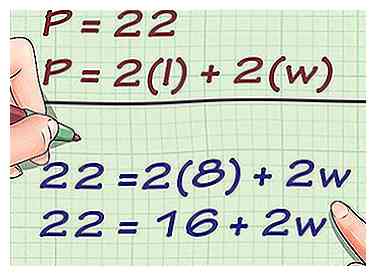 2 Steek de waarden voor omtrek en lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor omtrek en lengte in de formule. Zorg ervoor dat u de juiste variabelen vervangt.  3 Oplossen voor
3 Oplossen voor  4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
4 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen. 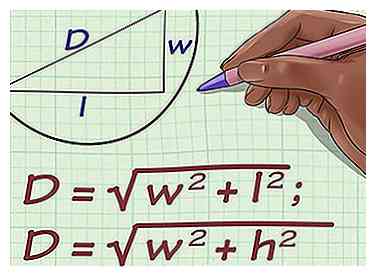 1 Stel de formule in voor de diagonaal van een rechthoek. De formule is
1 Stel de formule in voor de diagonaal van een rechthoek. De formule is  2 Steek de waarden voor de diagonaal en de lengte van de zijkant in de formule. Zorg ervoor dat u de juiste variabelen vervangt.
2 Steek de waarden voor de diagonaal en de lengte van de zijkant in de formule. Zorg ervoor dat u de juiste variabelen vervangt. 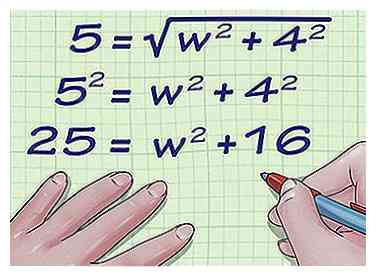 3 Vierkant van beide zijden van de formule. U moet dit doen om van het vierkantswortelbord af te komen, wat het isoleren van de breedtevariabele eenvoudiger maakt.
3 Vierkant van beide zijden van de formule. U moet dit doen om van het vierkantswortelbord af te komen, wat het isoleren van de breedtevariabele eenvoudiger maakt. 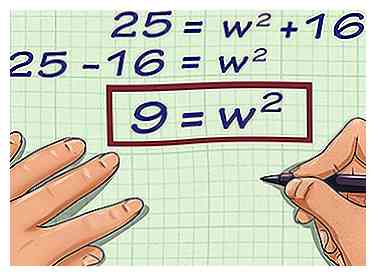 4 Isoleer de
4 Isoleer de  5 Oplossen voor
5 Oplossen voor  6 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.
6 Schrijf je laatste antwoord. Vergeet niet om de maateenheid op te nemen.  1 Stel de formule in voor het gebied of de omtrek van een rechthoek. Welke formule u gebruikt, hangt af van de meting die u krijgt. Als u het gebied krijgt, stelt u de gebiedformule in. Als u de perimeter krijgt, stelt u de perimeterformule in.
1 Stel de formule in voor het gebied of de omtrek van een rechthoek. Welke formule u gebruikt, hangt af van de meting die u krijgt. Als u het gebied krijgt, stelt u de gebiedformule in. Als u de perimeter krijgt, stelt u de perimeterformule in.  2 Schrijf de uitdrukking die de relatie tussen de lengte en de breedte beschrijft. Schrijf je expressie in termen van wat
2 Schrijf de uitdrukking die de relatie tussen de lengte en de breedte beschrijft. Schrijf je expressie in termen van wat 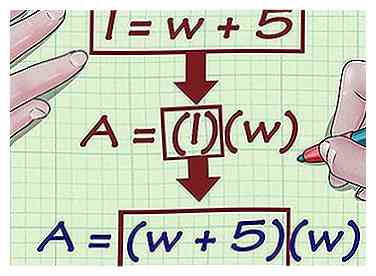 3 Vervang de
3 Vervang de  4 Vereenvoudig de vergelijking. Uw vereenvoudigde vergelijking kan verschillende vormen aannemen, afhankelijk van de relatie tussen de lengte en de breedte en afhankelijk van of u met een gebied of perimeter werkt.[7] Denk aan het opstellen van een vergelijking waarmee je kunt oplossen
4 Vereenvoudig de vergelijking. Uw vereenvoudigde vergelijking kan verschillende vormen aannemen, afhankelijk van de relatie tussen de lengte en de breedte en afhankelijk van of u met een gebied of perimeter werkt.[7] Denk aan het opstellen van een vergelijking waarmee je kunt oplossen 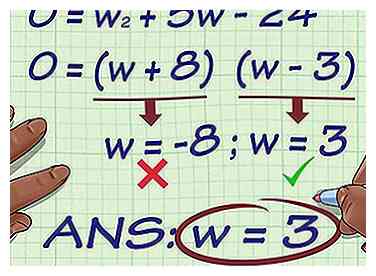 5 Oplossen voor
5 Oplossen voor