Een vijfhoek is een polygoon met vijf rechte zijden. Bijna alle problemen die je in de wiskundeles tegenkomt, hebben betrekking op gewone vijfhoeken, met vijf gelijke kanten. Er zijn twee veelgebruikte manieren om het gebied te vinden, afhankelijk van de hoeveelheid informatie die je hebt.
Methode één van de drie:
Het gebied vinden vanaf de zijkant Lengte en Apothem
-
 1 Begin met de lengte van de zijkant en apothem. Deze methode werkt voor gewone vijfhoeken, met vijf gelijke zijden. Naast de lengte van de zijkant heb je de "apothem" van de vijfhoek nodig. De apothem is de lijn van het midden van de vijfhoek naar een zijde, die de zijkant kruist in een rechte hoek van 90 °.
1 Begin met de lengte van de zijkant en apothem. Deze methode werkt voor gewone vijfhoeken, met vijf gelijke zijden. Naast de lengte van de zijkant heb je de "apothem" van de vijfhoek nodig. De apothem is de lijn van het midden van de vijfhoek naar een zijde, die de zijkant kruist in een rechte hoek van 90 °. - Verwar apothem niet met de straal, die een hoek (vertex) raakt in plaats van een middelpunt. Als u alleen de lengte en straal van de zijkant kent, gaat u naar de volgende methode.
- We gebruiken een voorbeeld vijfhoek met lengte van de zijkant 3 eenheden en apothem 2 units.
-
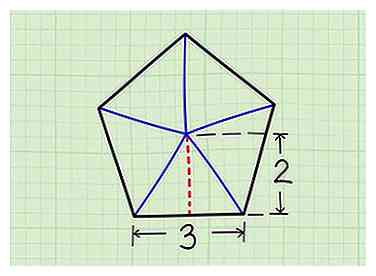 2 Verdeel de pentagon in vijf driehoeken. Teken vijf lijnen vanuit het midden van de vijfhoek, leidend tot elke hoekpunt (hoek). Je hebt nu vijf driehoeken.
2 Verdeel de pentagon in vijf driehoeken. Teken vijf lijnen vanuit het midden van de vijfhoek, leidend tot elke hoekpunt (hoek). Je hebt nu vijf driehoeken. -
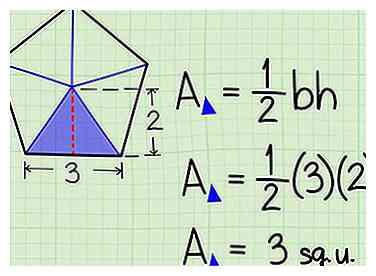 3 Bereken het gebied van een driehoek. Elke driehoek heeft een baseren gelijk aan de zijkant van de vijfhoek. Het heeft ook een hoogte gelijk aan de apothem van het pentagon. (Denk eraan, de hoogte van een driehoek loopt van een hoekpunt naar de andere kant, in een rechte hoek.) Bereken ½ x basis x hoogte om het gebied van een willekeurige driehoek te vinden.
3 Bereken het gebied van een driehoek. Elke driehoek heeft een baseren gelijk aan de zijkant van de vijfhoek. Het heeft ook een hoogte gelijk aan de apothem van het pentagon. (Denk eraan, de hoogte van een driehoek loopt van een hoekpunt naar de andere kant, in een rechte hoek.) Bereken ½ x basis x hoogte om het gebied van een willekeurige driehoek te vinden. - In ons voorbeeld, gebied van driehoek = ½ x 3 x 2 = 3 vierkante eenheden.
-
 4 Vermenigvuldig met vijf om het totale gebied te vinden. We hebben de vijfhoek verdeeld in vijf gelijke driehoeken. Om het totale gebied te vinden, vermenigvuldigt u het gebied van één driehoek met vijf.
4 Vermenigvuldig met vijf om het totale gebied te vinden. We hebben de vijfhoek verdeeld in vijf gelijke driehoeken. Om het totale gebied te vinden, vermenigvuldigt u het gebied van één driehoek met vijf. - In ons voorbeeld is A (totaal vijfhoek) = 5 x A (driehoek) = 5 x 3 = 15 vierkante eenheden.
Methode twee van drie:
Het gebied van opzij vinden
-
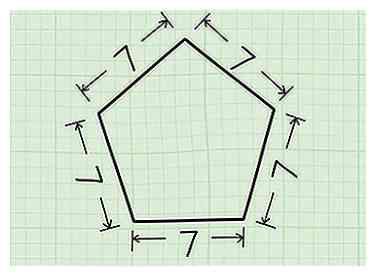 1 Begin met alleen de lengte van de zijkant. Deze methode werkt alleen voor gewone vijfhoeken, die vijf zijden van gelijke lengte hebben.
1 Begin met alleen de lengte van de zijkant. Deze methode werkt alleen voor gewone vijfhoeken, die vijf zijden van gelijke lengte hebben. - In dit voorbeeld gebruiken we een vijfhoek met de lengte van de zijkant 7 units.
-
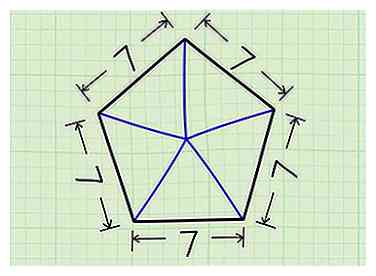 2 Verdeel de pentagon in vijf driehoeken. Trek een lijn vanuit het midden van de vijfhoek naar een hoekpunt. Herhaal dit voor elke vertex. Je hebt nu vijf driehoeken, elk van hetzelfde formaat.
2 Verdeel de pentagon in vijf driehoeken. Trek een lijn vanuit het midden van de vijfhoek naar een hoekpunt. Herhaal dit voor elke vertex. Je hebt nu vijf driehoeken, elk van hetzelfde formaat. -
 3 Verdeel een driehoek doormidden. Trek een lijn vanuit het midden van de vijfhoek naar de basis van één driehoek. Deze lijn moet de basis raken in een rechte hoek van 90º, en de driehoek verdelen in twee gelijke, kleinere driehoeken.
3 Verdeel een driehoek doormidden. Trek een lijn vanuit het midden van de vijfhoek naar de basis van één driehoek. Deze lijn moet de basis raken in een rechte hoek van 90º, en de driehoek verdelen in twee gelijke, kleinere driehoeken. -
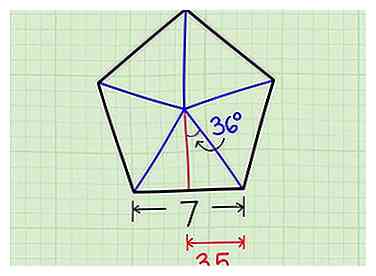 4 Label een van de kleinere driehoeken. We kunnen alvast een kant en een hoek van de kleinere driehoek labelen:
4 Label een van de kleinere driehoeken. We kunnen alvast een kant en een hoek van de kleinere driehoek labelen: - De baseren van de driehoek is ½ aan de zijkant van de vijfhoek. In ons voorbeeld is dit ½ x 7 = 3.5 eenheden.
- De hoek in het midden van de vijfhoek is altijd 36º.[1] (Beginnend met een volledig 360º centrum, zou je het in 10 van deze kleinere driehoeken kunnen verdelen. 360 ÷ 10 = 36, dus de hoek bij één driehoek is 36º.)
-
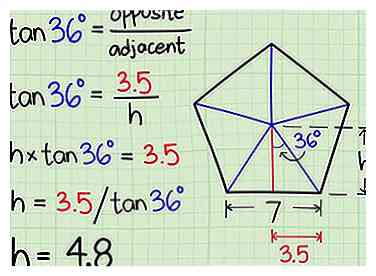 5 Bereken de hoogte van de driehoek. De hoogte van deze driehoek is de zijde haaks op de rand van het pentagon, die naar het midden leidt. We kunnen beginnende trigonometrie gebruiken om de lengte van deze zijde te vinden:[2]
5 Bereken de hoogte van de driehoek. De hoogte van deze driehoek is de zijde haaks op de rand van het pentagon, die naar het midden leidt. We kunnen beginnende trigonometrie gebruiken om de lengte van deze zijde te vinden:[2] - In een rechthoekige driehoek, de raaklijn van een hoek is gelijk aan de lengte van de tegenoverliggende zijde, gedeeld door de lengte van de aangrenzende zijde.
- De zijde tegenover de hoek van 36º is de basis van de driehoek (de helft van de zijde van de vijfhoek). De zijde naast de hoek van 36º is de hoogte van de driehoek.
- tan (36º) = tegenover / naast
- In ons voorbeeld is tan (36º) = 3,5 / hoogte
- hoogte x tan (36º) = 3,5
- hoogte = 3,5 / tan (36º)
- hoogte = (ongeveer) 4.8 units.
-
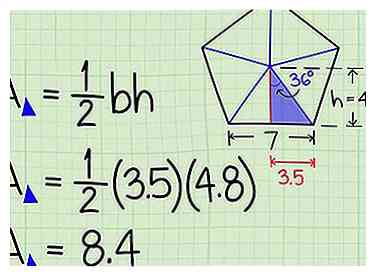 6 Zoek het gebied van de driehoek. Het gebied van een driehoek is gelijk aan ½ de basis x de hoogte. (A = ½bh.) Nu u de hoogte kent, sluit u deze waarden aan om het gebied van uw kleine driehoek te vinden.
6 Zoek het gebied van de driehoek. Het gebied van een driehoek is gelijk aan ½ de basis x de hoogte. (A = ½bh.) Nu u de hoogte kent, sluit u deze waarden aan om het gebied van uw kleine driehoek te vinden. - In ons voorbeeld is het gebied met de kleine driehoek = ½bh = ½ (3.5) (4.8) = 8.4 vierkante eenheden.
-
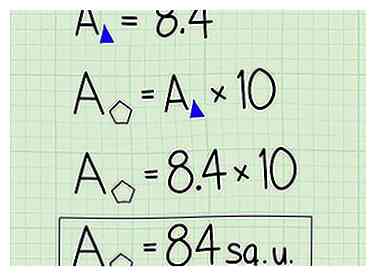 7 Vermenigvuldig om het gebied van de vijfhoek te vinden. Een van deze kleinere driehoeken beslaat 1/10 van het gebied van de vijfhoek. Om het totale gebied te vinden, vermenigvuldigt u het gebied van de kleinere driehoek met 10.
7 Vermenigvuldig om het gebied van de vijfhoek te vinden. Een van deze kleinere driehoeken beslaat 1/10 van het gebied van de vijfhoek. Om het totale gebied te vinden, vermenigvuldigt u het gebied van de kleinere driehoek met 10. - In ons voorbeeld is het gebied van de hele vijfhoek = 8.4 x 10 = 84 vierkante eenheden.
Methode drie van drie:
Een formule gebruiken
-
 1 Gebruik de omtrek en apothem. De apothem is een lijn vanuit het midden van een vijfhoek, die een zijde raakt in een rechte hoek. Als u de lengte ervan krijgt, kunt u deze eenvoudige formule gebruiken
1 Gebruik de omtrek en apothem. De apothem is een lijn vanuit het midden van een vijfhoek, die een zijde raakt in een rechte hoek. Als u de lengte ervan krijgt, kunt u deze eenvoudige formule gebruiken - Gebied van een regelmatige vijfhoek = vader/ 2, waar p = de omtrek en een = het apothem.[3]
- Als u de perimeter niet kent, bereken deze dan aan de hand van de lengte van de zijkant: p = 5s, waarbij s de lengte van de zijkant is.
-
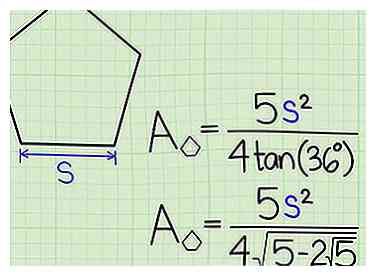 2 Gebruik de lengte van de zijkant. Als u alleen de lengte van de zijde kent, gebruikt u de volgende formule:[4]
2 Gebruik de lengte van de zijkant. Als u alleen de lengte van de zijde kent, gebruikt u de volgende formule:[4] - Gebied van een regelmatige vijfhoek = (5s2) / (4tan (36º)), waar s = lengte van de zijkant.
- tan (36º) = √ (5-2√5).[5] Dus als uw rekenmachine geen "tan" -functie heeft, gebruik dan de formule Area = (5s2) / (4√(5-2√5)).
-
 3 Kies een formule die alleen radius gebruikt. Je kunt het gebied zelfs vinden als je alleen de straal kent. Gebruik deze formule:[6]
3 Kies een formule die alleen radius gebruikt. Je kunt het gebied zelfs vinden als je alleen de straal kent. Gebruik deze formule:[6] - Gebied van een regelmatige vijfhoek = (5/2)r2sin (72º), waar r is de straal.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Begin met de lengte van de zijkant en apothem. Deze methode werkt voor gewone vijfhoeken, met vijf gelijke zijden. Naast de lengte van de zijkant heb je de "apothem" van de vijfhoek nodig. De apothem is de lijn van het midden van de vijfhoek naar een zijde, die de zijkant kruist in een rechte hoek van 90 °.
1 Begin met de lengte van de zijkant en apothem. Deze methode werkt voor gewone vijfhoeken, met vijf gelijke zijden. Naast de lengte van de zijkant heb je de "apothem" van de vijfhoek nodig. De apothem is de lijn van het midden van de vijfhoek naar een zijde, die de zijkant kruist in een rechte hoek van 90 °.  2 Verdeel de pentagon in vijf driehoeken. Teken vijf lijnen vanuit het midden van de vijfhoek, leidend tot elke hoekpunt (hoek). Je hebt nu vijf driehoeken.
2 Verdeel de pentagon in vijf driehoeken. Teken vijf lijnen vanuit het midden van de vijfhoek, leidend tot elke hoekpunt (hoek). Je hebt nu vijf driehoeken.  3 Bereken het gebied van een driehoek. Elke driehoek heeft een baseren gelijk aan de zijkant van de vijfhoek. Het heeft ook een hoogte gelijk aan de apothem van het pentagon. (Denk eraan, de hoogte van een driehoek loopt van een hoekpunt naar de andere kant, in een rechte hoek.) Bereken ½ x basis x hoogte om het gebied van een willekeurige driehoek te vinden.
3 Bereken het gebied van een driehoek. Elke driehoek heeft een baseren gelijk aan de zijkant van de vijfhoek. Het heeft ook een hoogte gelijk aan de apothem van het pentagon. (Denk eraan, de hoogte van een driehoek loopt van een hoekpunt naar de andere kant, in een rechte hoek.) Bereken ½ x basis x hoogte om het gebied van een willekeurige driehoek te vinden.  4 Vermenigvuldig met vijf om het totale gebied te vinden. We hebben de vijfhoek verdeeld in vijf gelijke driehoeken. Om het totale gebied te vinden, vermenigvuldigt u het gebied van één driehoek met vijf.
4 Vermenigvuldig met vijf om het totale gebied te vinden. We hebben de vijfhoek verdeeld in vijf gelijke driehoeken. Om het totale gebied te vinden, vermenigvuldigt u het gebied van één driehoek met vijf.  1 Begin met alleen de lengte van de zijkant. Deze methode werkt alleen voor gewone vijfhoeken, die vijf zijden van gelijke lengte hebben.
1 Begin met alleen de lengte van de zijkant. Deze methode werkt alleen voor gewone vijfhoeken, die vijf zijden van gelijke lengte hebben.  2 Verdeel de pentagon in vijf driehoeken. Trek een lijn vanuit het midden van de vijfhoek naar een hoekpunt. Herhaal dit voor elke vertex. Je hebt nu vijf driehoeken, elk van hetzelfde formaat.
2 Verdeel de pentagon in vijf driehoeken. Trek een lijn vanuit het midden van de vijfhoek naar een hoekpunt. Herhaal dit voor elke vertex. Je hebt nu vijf driehoeken, elk van hetzelfde formaat.  3 Verdeel een driehoek doormidden. Trek een lijn vanuit het midden van de vijfhoek naar de basis van één driehoek. Deze lijn moet de basis raken in een rechte hoek van 90º, en de driehoek verdelen in twee gelijke, kleinere driehoeken.
3 Verdeel een driehoek doormidden. Trek een lijn vanuit het midden van de vijfhoek naar de basis van één driehoek. Deze lijn moet de basis raken in een rechte hoek van 90º, en de driehoek verdelen in twee gelijke, kleinere driehoeken.  4 Label een van de kleinere driehoeken. We kunnen alvast een kant en een hoek van de kleinere driehoek labelen:
4 Label een van de kleinere driehoeken. We kunnen alvast een kant en een hoek van de kleinere driehoek labelen:  5 Bereken de hoogte van de driehoek. De hoogte van deze driehoek is de zijde haaks op de rand van het pentagon, die naar het midden leidt. We kunnen beginnende trigonometrie gebruiken om de lengte van deze zijde te vinden:[2]
5 Bereken de hoogte van de driehoek. De hoogte van deze driehoek is de zijde haaks op de rand van het pentagon, die naar het midden leidt. We kunnen beginnende trigonometrie gebruiken om de lengte van deze zijde te vinden:[2] 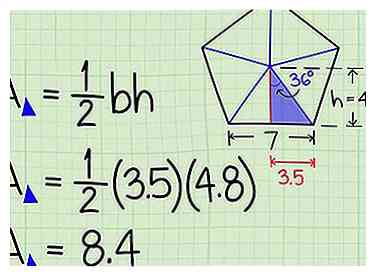 6 Zoek het gebied van de driehoek. Het gebied van een driehoek is gelijk aan ½ de basis x de hoogte. (A = ½bh.) Nu u de hoogte kent, sluit u deze waarden aan om het gebied van uw kleine driehoek te vinden.
6 Zoek het gebied van de driehoek. Het gebied van een driehoek is gelijk aan ½ de basis x de hoogte. (A = ½bh.) Nu u de hoogte kent, sluit u deze waarden aan om het gebied van uw kleine driehoek te vinden. 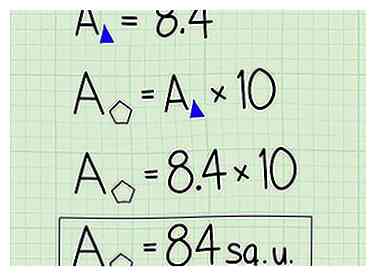 7 Vermenigvuldig om het gebied van de vijfhoek te vinden. Een van deze kleinere driehoeken beslaat 1/10 van het gebied van de vijfhoek. Om het totale gebied te vinden, vermenigvuldigt u het gebied van de kleinere driehoek met 10.
7 Vermenigvuldig om het gebied van de vijfhoek te vinden. Een van deze kleinere driehoeken beslaat 1/10 van het gebied van de vijfhoek. Om het totale gebied te vinden, vermenigvuldigt u het gebied van de kleinere driehoek met 10.  1 Gebruik de omtrek en apothem. De apothem is een lijn vanuit het midden van een vijfhoek, die een zijde raakt in een rechte hoek. Als u de lengte ervan krijgt, kunt u deze eenvoudige formule gebruiken
1 Gebruik de omtrek en apothem. De apothem is een lijn vanuit het midden van een vijfhoek, die een zijde raakt in een rechte hoek. Als u de lengte ervan krijgt, kunt u deze eenvoudige formule gebruiken  2 Gebruik de lengte van de zijkant. Als u alleen de lengte van de zijde kent, gebruikt u de volgende formule:[4]
2 Gebruik de lengte van de zijkant. Als u alleen de lengte van de zijde kent, gebruikt u de volgende formule:[4]  3 Kies een formule die alleen radius gebruikt. Je kunt het gebied zelfs vinden als je alleen de straal kent. Gebruik deze formule:[6]
3 Kies een formule die alleen radius gebruikt. Je kunt het gebied zelfs vinden als je alleen de straal kent. Gebruik deze formule:[6]