Een gelijkbenige driehoek is een driehoek met twee zijden van dezelfde lengte. Deze twee gelijke zijden verbinden zich altijd onder dezelfde hoek met de basis (de derde zijde) en komen direct boven het middelpunt van de basis samen. Je kunt dit zelf testen met een liniaal en twee potloden van gelijke lengte: als je de driehoek in de ene of de andere richting probeert te kantelen, kun je niet krijgen dat de uiteinden van de potloden elkaar raken. Met deze speciale eigenschappen van de gelijkbenige driehoek kun je het gebied uit slechts een paar stukjes informatie berekenen.
Methode één van de twee:
Het gebied van de lengten van de zijkant vinden
-
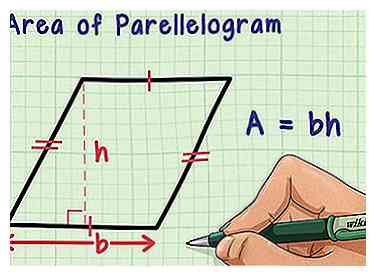 1 Beoordeel het gebied van een parallellogram. Vierkanten en rechthoeken zijn parallellogrammen, evenals elke vierzijdige vorm met twee sets evenwijdige zijden. Alle parallellogrammen hebben een eenvoudige gebiedformule: oppervlakte is gelijk aan basis vermenigvuldigd met de hoogte, of A = bh.[1] Als u het parallellogram plat op een horizontaal oppervlak plaatst, is de basis de lengte van de zijde waarop deze staat. De hoogte (zoals je zou verwachten) is hoe hoog hij van de grond is: de afstand van de basis naar de andere kant. Meet altijd de hoogte in een rechte hoek (90 graden) ten opzichte van de basis.
1 Beoordeel het gebied van een parallellogram. Vierkanten en rechthoeken zijn parallellogrammen, evenals elke vierzijdige vorm met twee sets evenwijdige zijden. Alle parallellogrammen hebben een eenvoudige gebiedformule: oppervlakte is gelijk aan basis vermenigvuldigd met de hoogte, of A = bh.[1] Als u het parallellogram plat op een horizontaal oppervlak plaatst, is de basis de lengte van de zijde waarop deze staat. De hoogte (zoals je zou verwachten) is hoe hoog hij van de grond is: de afstand van de basis naar de andere kant. Meet altijd de hoogte in een rechte hoek (90 graden) ten opzichte van de basis. - In vierkanten en rechthoeken is de hoogte gelijk aan de lengte van een verticale zijde, omdat deze zijden haaks op de grond staan.
-
 2 Vergelijk driehoeken en parallellogrammen. Er is een eenvoudige relatie tussen deze twee vormen. Knip een parallellogram doormidden langs de diagonaal en het splitst in twee gelijke driehoeken. Evenzo, als je twee identieke driehoeken hebt, kun je ze altijd samen plakken om een parallellogram te maken. Dit betekent dat het gebied van elke driehoek kan worden geschreven als A = ½bh, precies de helft van de grootte van een overeenkomstig parallellogram.
2 Vergelijk driehoeken en parallellogrammen. Er is een eenvoudige relatie tussen deze twee vormen. Knip een parallellogram doormidden langs de diagonaal en het splitst in twee gelijke driehoeken. Evenzo, als je twee identieke driehoeken hebt, kun je ze altijd samen plakken om een parallellogram te maken. Dit betekent dat het gebied van elke driehoek kan worden geschreven als A = ½bh, precies de helft van de grootte van een overeenkomstig parallellogram. -
 3 Zoek de basis van de gelijkbenige driehoek. Nu heb je de formule, maar wat betekent "base" en "height" precies in een gelijkbenige driehoek? De basis is het makkelijke gedeelte: gebruik gewoon de derde, ongelijke kant van de gelijkbenige.
3 Zoek de basis van de gelijkbenige driehoek. Nu heb je de formule, maar wat betekent "base" en "height" precies in een gelijkbenige driehoek? De basis is het makkelijke gedeelte: gebruik gewoon de derde, ongelijke kant van de gelijkbenige. - Als uw gelijkbenige driehoek bijvoorbeeld zijden heeft van 5 centimeter, 5 cm en 6 cm, gebruikt u 6 cm als basis.
- Als je driehoek drie gelijke zijden heeft (gelijkzijdig), kun je degene kiezen die de basis is. Een gelijkzijdige driehoek is een speciaal type gelijkbenig, maar je kunt het gebied op dezelfde manier vinden.[2]
-
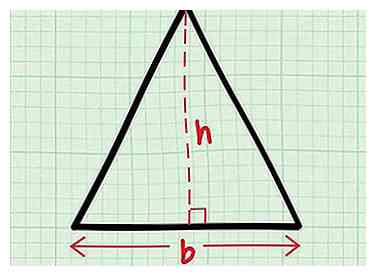 4 Teken een lijn tussen de basis en de tegenovergestelde hoek. Zorg ervoor dat de lijn de basis raakt in een rechte hoek. De lengte van deze lijn is de hoogte van je driehoek, dus label hem h. Zodra u de waarde van hebt berekend h, je zult het gebied kunnen vinden.
4 Teken een lijn tussen de basis en de tegenovergestelde hoek. Zorg ervoor dat de lijn de basis raakt in een rechte hoek. De lengte van deze lijn is de hoogte van je driehoek, dus label hem h. Zodra u de waarde van hebt berekend h, je zult het gebied kunnen vinden. - In een gelijkbenige driehoek raakt deze lijn altijd de basis op het exacte middelpunt.
-
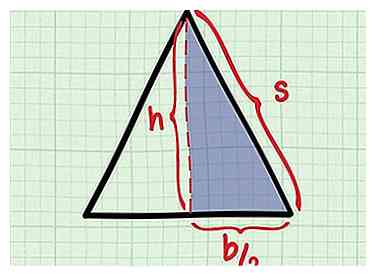 5 Kijk naar de helft van je gelijkbenige driehoek. U ziet dat de hoogtelijn uw gelijkbenige driehoek verdeelt in twee identieke rechthoekige driehoeken. Kijk naar een van hen en identificeer de drie kanten:
5 Kijk naar de helft van je gelijkbenige driehoek. U ziet dat de hoogtelijn uw gelijkbenige driehoek verdeelt in twee identieke rechthoekige driehoeken. Kijk naar een van hen en identificeer de drie kanten: - Een van de korte zijden is gelijk aan de helft van de basis: .
- De andere korte zijde is de hoogte, h.
- De hypotenusa van de rechthoekige driehoek is een van de twee gelijke zijden van de gelijkbenige. Laten we het noemen s.
-
 6 Zet de stelling van Pythagoras op. Telkens wanneer u twee zijden van een rechthoekige driehoek kent en de derde wilt vinden, kunt u de stelling van Pythagoras gebruiken: (zijde 1)2 + (zijde 2)2 = (hypotenusa)2 Vervang de variabelen die we gebruiken om dit probleem te krijgen .
6 Zet de stelling van Pythagoras op. Telkens wanneer u twee zijden van een rechthoekige driehoek kent en de derde wilt vinden, kunt u de stelling van Pythagoras gebruiken: (zijde 1)2 + (zijde 2)2 = (hypotenusa)2 Vervang de variabelen die we gebruiken om dit probleem te krijgen . - Je hebt waarschijnlijk de stelling van Pythagoras geleerd als . Het schrijven als "sides" en "hypotenusa" voorkomt verwarring met de variabelen van uw driehoek.
-
 7 Oplossen voor h. Vergeet niet dat de gebiedsformule gebruikt wordt b en h, maar je weet de waarde niet van h nog. Herschik de formule om op te lossen h:
7 Oplossen voor h. Vergeet niet dat de gebiedsformule gebruikt wordt b en h, maar je weet de waarde niet van h nog. Herschik de formule om op te lossen h: -
.
-
-
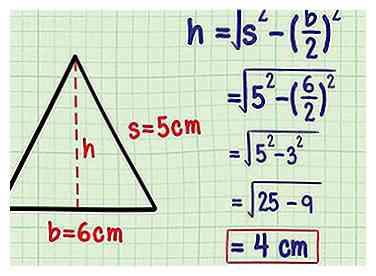 8 Sluit de waarden voor uw driehoek in om te vinden h. Nu je deze formule kent, kun je hem gebruiken voor elke gelijkbenige driehoek waar je de zijkanten kent. Plug gewoon de lengte van de basis in b en de lengte van een van de gelijke zijden voor s, bereken vervolgens de waarde van h.
8 Sluit de waarden voor uw driehoek in om te vinden h. Nu je deze formule kent, kun je hem gebruiken voor elke gelijkbenige driehoek waar je de zijkanten kent. Plug gewoon de lengte van de basis in b en de lengte van een van de gelijke zijden voor s, bereken vervolgens de waarde van h. - U hebt bijvoorbeeld een gelijkbenige driehoek met zijden van 5 cm, 5 cm en 6 cm. b = 6 en s = 5.
- Vervang deze in uw formule:
cm.
-
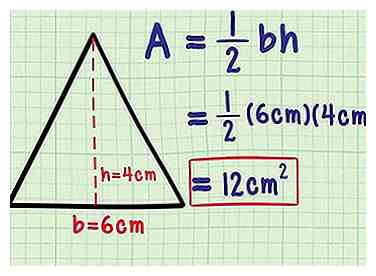 9 Steek de basis en hoogte in uw gebiedsformule. Nu heb je wat je nodig hebt om de formule te gebruiken vanaf het begin van dit gedeelte: Area = ½bh. Sluit gewoon de waarden die u hebt gevonden voor b en h in deze formule in en bereken het antwoord. Vergeet niet om uw antwoord te schrijven in termen van vierkante eenheden.
9 Steek de basis en hoogte in uw gebiedsformule. Nu heb je wat je nodig hebt om de formule te gebruiken vanaf het begin van dit gedeelte: Area = ½bh. Sluit gewoon de waarden die u hebt gevonden voor b en h in deze formule in en bereken het antwoord. Vergeet niet om uw antwoord te schrijven in termen van vierkante eenheden. - Om het voorbeeld voort te zetten, had de 5-5-6 driehoek een basis van 6 cm en een hoogte van 4 cm.
- A = ½bh
A = ½ (6 cm) (4 cm)
A = 12 cm2.
-
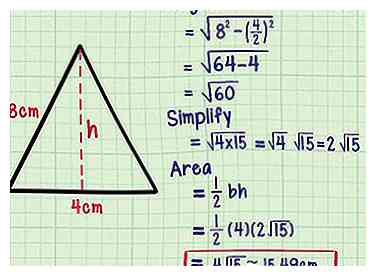 10 Probeer een moeilijker voorbeeld. De meeste gelijkbenige driehoeken zijn moeilijker om mee te werken dan het laatste voorbeeld. De hoogte bevat vaak een vierkantswortel die niet vereenvoudigt tot een geheel getal. Als dit gebeurt, laat de hoogte dan als een vierkantswortel in de eenvoudigste vorm. Hier is een voorbeeld:
10 Probeer een moeilijker voorbeeld. De meeste gelijkbenige driehoeken zijn moeilijker om mee te werken dan het laatste voorbeeld. De hoogte bevat vaak een vierkantswortel die niet vereenvoudigt tot een geheel getal. Als dit gebeurt, laat de hoogte dan als een vierkantswortel in de eenvoudigste vorm. Hier is een voorbeeld: - Wat is het gebied van een driehoek met zijden van 8 cm, 8 cm en 4 cm?
- Laat de ongelijke zijde, 4 cm, de basis zijn b.
- De hoogte
- Vereenvoudig de wortel door factoren te vinden:
- Gebied
- Laat dit antwoord zoals geschreven staan of voer het in op een rekenmachine om een decimale schatting te vinden (ongeveer 15,49 vierkante centimeter).
Methode twee van twee:
Goniometrie gebruiken
-
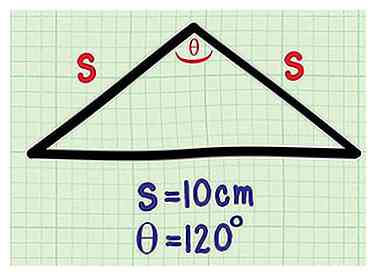 1 Begin met een zijde en een hoek. Als u enige trigonometrie kent, kunt u de oppervlakte van een gelijkbenige driehoek vinden, zelfs als u de lengte van een van de zijden niet kent. Dit is een voorbeeldprobleem waarbij u alleen het volgende kent:[3]
1 Begin met een zijde en een hoek. Als u enige trigonometrie kent, kunt u de oppervlakte van een gelijkbenige driehoek vinden, zelfs als u de lengte van een van de zijden niet kent. Dit is een voorbeeldprobleem waarbij u alleen het volgende kent:[3] - De lengte s van de twee gelijke zijden is 10 cm.
- De hoek θ tussen de twee gelijke zijden is 120 graden.
-
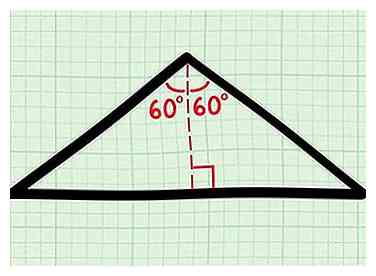 2 Verdeel de gelijkbenige in twee rechthoekige driehoeken. Trek een lijn naar beneden vanaf de top tussen de twee gelijke zijden, die de basis raakt in een rechte hoek. Je hebt nu twee gelijke rechthoekige driehoeken.
2 Verdeel de gelijkbenige in twee rechthoekige driehoeken. Trek een lijn naar beneden vanaf de top tussen de twee gelijke zijden, die de basis raakt in een rechte hoek. Je hebt nu twee gelijke rechthoekige driehoeken. - Deze lijn verdeelt θ perfect in twee. Elke rechthoekige driehoek heeft een hoek van ½θ, of in dit geval (½) (120) = 60 graden.
-
 3 Gebruik trigonometrie om de waarde van te vinden h. Nu dat u een rechthoekige driehoek hebt, kunt u de trigonometrische functies sinus, cosinus en tangens gebruiken. In het voorbeeldprobleem kent u de hypotenusa en wilt u de waarde van h, de zijde grenzend aan de bekende hoek. Gebruik het feit dat cosinus = aangrenzende / hypotenusa op te lossen h:
3 Gebruik trigonometrie om de waarde van te vinden h. Nu dat u een rechthoekige driehoek hebt, kunt u de trigonometrische functies sinus, cosinus en tangens gebruiken. In het voorbeeldprobleem kent u de hypotenusa en wilt u de waarde van h, de zijde grenzend aan de bekende hoek. Gebruik het feit dat cosinus = aangrenzende / hypotenusa op te lossen h: - cos (θ / 2) = h / s
- cos (60º) = h / 10
- h = 10cos (60º)
-
 4 Zoek de waarde van de overgebleven kant. Er is één resterende onbekende kant van de rechthoekige driehoek, die u kunt oproepen X. Los dit op met behulp van de definitie sine = tegenover / hypotenusa:
4 Zoek de waarde van de overgebleven kant. Er is één resterende onbekende kant van de rechthoekige driehoek, die u kunt oproepen X. Los dit op met behulp van de definitie sine = tegenover / hypotenusa: - sin (θ / 2) = x / s
- sin (60º) = x / 10
- x = 10sin (60º)
-
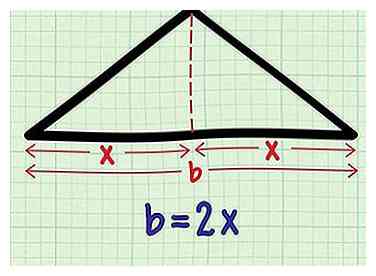 5 Verbind x met de basis van de gelijkbenige driehoek. U kunt nu "uitzoomen" naar de belangrijkste gelijkbenige driehoek. De totale basis b is gelijk aan 2X, omdat het was verdeeld in twee segmenten met elk een lengte van X.
5 Verbind x met de basis van de gelijkbenige driehoek. U kunt nu "uitzoomen" naar de belangrijkste gelijkbenige driehoek. De totale basis b is gelijk aan 2X, omdat het was verdeeld in twee segmenten met elk een lengte van X. -
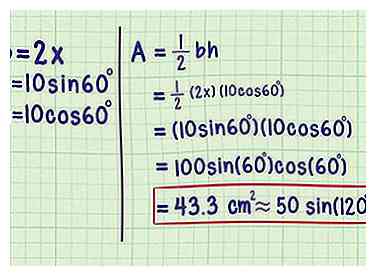 6 Sluit uw waarden aan voor h en b in de basisgebiedformule. Nu u de basis en hoogte kent, kunt u vertrouwen op de standaardformule A = ½bh:
6 Sluit uw waarden aan voor h en b in de basisgebiedformule. Nu u de basis en hoogte kent, kunt u vertrouwen op de standaardformule A = ½bh: -
- U kunt dit invoeren in een rekenmachine (ingesteld op graden), waarmee u een antwoord krijgt van ongeveer 43,3 vierkante centimeter. U kunt ook eigenschappen van trigonometrie gebruiken om het te vereenvoudigen tot A = 50sin (120º).
-
-
 7 Verander dit in een universele formule. Nu u weet hoe dit is opgelost, kunt u vertrouwen op de algemene formule zonder elke keer het volledige proces te doorlopen. Dit is wat u uiteindelijk krijgt als u dit proces herhaalt zonder specifieke waarden te gebruiken (en het gebruik van eigenschappen van trigonometrie te vereenvoudigen):[4]
7 Verander dit in een universele formule. Nu u weet hoe dit is opgelost, kunt u vertrouwen op de algemene formule zonder elke keer het volledige proces te doorlopen. Dit is wat u uiteindelijk krijgt als u dit proces herhaalt zonder specifieke waarden te gebruiken (en het gebruik van eigenschappen van trigonometrie te vereenvoudigen):[4] - s is de lengte van een van de twee gelijke zijden.
- θ is de hoek tussen de twee gelijke zijden.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Beoordeel het gebied van een parallellogram. Vierkanten en rechthoeken zijn parallellogrammen, evenals elke vierzijdige vorm met twee sets evenwijdige zijden. Alle parallellogrammen hebben een eenvoudige gebiedformule: oppervlakte is gelijk aan basis vermenigvuldigd met de hoogte, of A = bh.[1] Als u het parallellogram plat op een horizontaal oppervlak plaatst, is de basis de lengte van de zijde waarop deze staat. De hoogte (zoals je zou verwachten) is hoe hoog hij van de grond is: de afstand van de basis naar de andere kant. Meet altijd de hoogte in een rechte hoek (90 graden) ten opzichte van de basis.
1 Beoordeel het gebied van een parallellogram. Vierkanten en rechthoeken zijn parallellogrammen, evenals elke vierzijdige vorm met twee sets evenwijdige zijden. Alle parallellogrammen hebben een eenvoudige gebiedformule: oppervlakte is gelijk aan basis vermenigvuldigd met de hoogte, of A = bh.[1] Als u het parallellogram plat op een horizontaal oppervlak plaatst, is de basis de lengte van de zijde waarop deze staat. De hoogte (zoals je zou verwachten) is hoe hoog hij van de grond is: de afstand van de basis naar de andere kant. Meet altijd de hoogte in een rechte hoek (90 graden) ten opzichte van de basis.  2 Vergelijk driehoeken en parallellogrammen. Er is een eenvoudige relatie tussen deze twee vormen. Knip een parallellogram doormidden langs de diagonaal en het splitst in twee gelijke driehoeken. Evenzo, als je twee identieke driehoeken hebt, kun je ze altijd samen plakken om een parallellogram te maken. Dit betekent dat het gebied van elke driehoek kan worden geschreven als A = ½bh, precies de helft van de grootte van een overeenkomstig parallellogram.
2 Vergelijk driehoeken en parallellogrammen. Er is een eenvoudige relatie tussen deze twee vormen. Knip een parallellogram doormidden langs de diagonaal en het splitst in twee gelijke driehoeken. Evenzo, als je twee identieke driehoeken hebt, kun je ze altijd samen plakken om een parallellogram te maken. Dit betekent dat het gebied van elke driehoek kan worden geschreven als A = ½bh, precies de helft van de grootte van een overeenkomstig parallellogram.  3 Zoek de basis van de gelijkbenige driehoek. Nu heb je de formule, maar wat betekent "base" en "height" precies in een gelijkbenige driehoek? De basis is het makkelijke gedeelte: gebruik gewoon de derde, ongelijke kant van de gelijkbenige.
3 Zoek de basis van de gelijkbenige driehoek. Nu heb je de formule, maar wat betekent "base" en "height" precies in een gelijkbenige driehoek? De basis is het makkelijke gedeelte: gebruik gewoon de derde, ongelijke kant van de gelijkbenige.  4 Teken een lijn tussen de basis en de tegenovergestelde hoek. Zorg ervoor dat de lijn de basis raakt in een rechte hoek. De lengte van deze lijn is de hoogte van je driehoek, dus label hem h. Zodra u de waarde van hebt berekend h, je zult het gebied kunnen vinden.
4 Teken een lijn tussen de basis en de tegenovergestelde hoek. Zorg ervoor dat de lijn de basis raakt in een rechte hoek. De lengte van deze lijn is de hoogte van je driehoek, dus label hem h. Zodra u de waarde van hebt berekend h, je zult het gebied kunnen vinden.  5 Kijk naar de helft van je gelijkbenige driehoek. U ziet dat de hoogtelijn uw gelijkbenige driehoek verdeelt in twee identieke rechthoekige driehoeken. Kijk naar een van hen en identificeer de drie kanten:
5 Kijk naar de helft van je gelijkbenige driehoek. U ziet dat de hoogtelijn uw gelijkbenige driehoek verdeelt in twee identieke rechthoekige driehoeken. Kijk naar een van hen en identificeer de drie kanten:  6 Zet de stelling van Pythagoras op. Telkens wanneer u twee zijden van een rechthoekige driehoek kent en de derde wilt vinden, kunt u de stelling van Pythagoras gebruiken: (zijde 1)2 + (zijde 2)2 = (hypotenusa)2 Vervang de variabelen die we gebruiken om dit probleem te krijgen
6 Zet de stelling van Pythagoras op. Telkens wanneer u twee zijden van een rechthoekige driehoek kent en de derde wilt vinden, kunt u de stelling van Pythagoras gebruiken: (zijde 1)2 + (zijde 2)2 = (hypotenusa)2 Vervang de variabelen die we gebruiken om dit probleem te krijgen  7 Oplossen voor h. Vergeet niet dat de gebiedsformule gebruikt wordt b en h, maar je weet de waarde niet van h nog. Herschik de formule om op te lossen h:
7 Oplossen voor h. Vergeet niet dat de gebiedsformule gebruikt wordt b en h, maar je weet de waarde niet van h nog. Herschik de formule om op te lossen h:  8 Sluit de waarden voor uw driehoek in om te vinden h. Nu je deze formule kent, kun je hem gebruiken voor elke gelijkbenige driehoek waar je de zijkanten kent. Plug gewoon de lengte van de basis in b en de lengte van een van de gelijke zijden voor s, bereken vervolgens de waarde van h.
8 Sluit de waarden voor uw driehoek in om te vinden h. Nu je deze formule kent, kun je hem gebruiken voor elke gelijkbenige driehoek waar je de zijkanten kent. Plug gewoon de lengte van de basis in b en de lengte van een van de gelijke zijden voor s, bereken vervolgens de waarde van h.  9 Steek de basis en hoogte in uw gebiedsformule. Nu heb je wat je nodig hebt om de formule te gebruiken vanaf het begin van dit gedeelte: Area = ½bh. Sluit gewoon de waarden die u hebt gevonden voor b en h in deze formule in en bereken het antwoord. Vergeet niet om uw antwoord te schrijven in termen van vierkante eenheden.
9 Steek de basis en hoogte in uw gebiedsformule. Nu heb je wat je nodig hebt om de formule te gebruiken vanaf het begin van dit gedeelte: Area = ½bh. Sluit gewoon de waarden die u hebt gevonden voor b en h in deze formule in en bereken het antwoord. Vergeet niet om uw antwoord te schrijven in termen van vierkante eenheden.  10 Probeer een moeilijker voorbeeld. De meeste gelijkbenige driehoeken zijn moeilijker om mee te werken dan het laatste voorbeeld. De hoogte bevat vaak een vierkantswortel die niet vereenvoudigt tot een geheel getal. Als dit gebeurt, laat de hoogte dan als een vierkantswortel in de eenvoudigste vorm. Hier is een voorbeeld:
10 Probeer een moeilijker voorbeeld. De meeste gelijkbenige driehoeken zijn moeilijker om mee te werken dan het laatste voorbeeld. De hoogte bevat vaak een vierkantswortel die niet vereenvoudigt tot een geheel getal. Als dit gebeurt, laat de hoogte dan als een vierkantswortel in de eenvoudigste vorm. Hier is een voorbeeld:  1 Begin met een zijde en een hoek. Als u enige trigonometrie kent, kunt u de oppervlakte van een gelijkbenige driehoek vinden, zelfs als u de lengte van een van de zijden niet kent. Dit is een voorbeeldprobleem waarbij u alleen het volgende kent:[3]
1 Begin met een zijde en een hoek. Als u enige trigonometrie kent, kunt u de oppervlakte van een gelijkbenige driehoek vinden, zelfs als u de lengte van een van de zijden niet kent. Dit is een voorbeeldprobleem waarbij u alleen het volgende kent:[3]  2 Verdeel de gelijkbenige in twee rechthoekige driehoeken. Trek een lijn naar beneden vanaf de top tussen de twee gelijke zijden, die de basis raakt in een rechte hoek. Je hebt nu twee gelijke rechthoekige driehoeken.
2 Verdeel de gelijkbenige in twee rechthoekige driehoeken. Trek een lijn naar beneden vanaf de top tussen de twee gelijke zijden, die de basis raakt in een rechte hoek. Je hebt nu twee gelijke rechthoekige driehoeken.  3 Gebruik trigonometrie om de waarde van te vinden h. Nu dat u een rechthoekige driehoek hebt, kunt u de trigonometrische functies sinus, cosinus en tangens gebruiken. In het voorbeeldprobleem kent u de hypotenusa en wilt u de waarde van h, de zijde grenzend aan de bekende hoek. Gebruik het feit dat cosinus = aangrenzende / hypotenusa op te lossen h:
3 Gebruik trigonometrie om de waarde van te vinden h. Nu dat u een rechthoekige driehoek hebt, kunt u de trigonometrische functies sinus, cosinus en tangens gebruiken. In het voorbeeldprobleem kent u de hypotenusa en wilt u de waarde van h, de zijde grenzend aan de bekende hoek. Gebruik het feit dat cosinus = aangrenzende / hypotenusa op te lossen h:  4 Zoek de waarde van de overgebleven kant. Er is één resterende onbekende kant van de rechthoekige driehoek, die u kunt oproepen X. Los dit op met behulp van de definitie sine = tegenover / hypotenusa:
4 Zoek de waarde van de overgebleven kant. Er is één resterende onbekende kant van de rechthoekige driehoek, die u kunt oproepen X. Los dit op met behulp van de definitie sine = tegenover / hypotenusa:  5 Verbind x met de basis van de gelijkbenige driehoek. U kunt nu "uitzoomen" naar de belangrijkste gelijkbenige driehoek. De totale basis b is gelijk aan 2X, omdat het was verdeeld in twee segmenten met elk een lengte van X.
5 Verbind x met de basis van de gelijkbenige driehoek. U kunt nu "uitzoomen" naar de belangrijkste gelijkbenige driehoek. De totale basis b is gelijk aan 2X, omdat het was verdeeld in twee segmenten met elk een lengte van X. 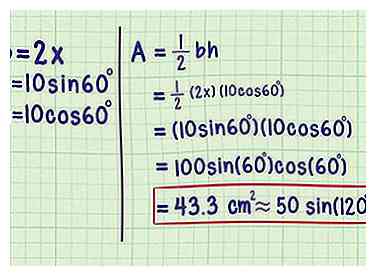 6 Sluit uw waarden aan voor h en b in de basisgebiedformule. Nu u de basis en hoogte kent, kunt u vertrouwen op de standaardformule A = ½bh:
6 Sluit uw waarden aan voor h en b in de basisgebiedformule. Nu u de basis en hoogte kent, kunt u vertrouwen op de standaardformule A = ½bh:  7 Verander dit in een universele formule. Nu u weet hoe dit is opgelost, kunt u vertrouwen op de algemene formule zonder elke keer het volledige proces te doorlopen. Dit is wat u uiteindelijk krijgt als u dit proces herhaalt zonder specifieke waarden te gebruiken (en het gebruik van eigenschappen van trigonometrie te vereenvoudigen):[4]
7 Verander dit in een universele formule. Nu u weet hoe dit is opgelost, kunt u vertrouwen op de algemene formule zonder elke keer het volledige proces te doorlopen. Dit is wat u uiteindelijk krijgt als u dit proces herhaalt zonder specifieke waarden te gebruiken (en het gebruik van eigenschappen van trigonometrie te vereenvoudigen):[4]