Een matrix is een rechthoekige rangschikking van getallen, symbolen of uitdrukkingen in rijen en kolommen. Als u matrices wilt vermenigvuldigen, moet u de elementen (of getallen) in de rij van de eerste matrix vermenigvuldigen met de elementen in de rijen van de tweede matrix en hun producten toevoegen. U kunt matrices in slechts een paar eenvoudige stappen vermenigvuldigen die toevoeging, vermenigvuldiging en de juiste plaatsing van de resultaten vereisen.
Stappen
-
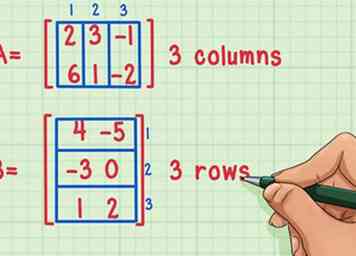 1 Controleer of de matrices kunnen worden vermenigvuldigd. U kunt matrices alleen vermenigvuldigen als het aantal kolommen van de eerste matrix gelijk is aan het aantal rijen in de tweede matrix.
1 Controleer of de matrices kunnen worden vermenigvuldigd. U kunt matrices alleen vermenigvuldigen als het aantal kolommen van de eerste matrix gelijk is aan het aantal rijen in de tweede matrix. - Deze matrices kunnen worden vermenigvuldigd omdat de eerste matrix, matrix A, 3 kolommen heeft, terwijl de tweede matrix, matrix B, 3 rijen heeft.
-
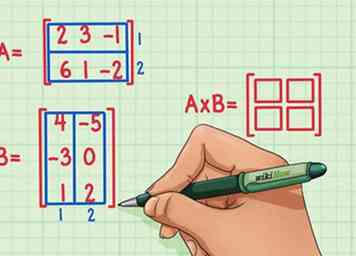 2 Markeer de afmetingen van het matrixproduct. Maak een nieuwe lege matrix die de afmetingen van het matrixproduct, het product van de twee matrices, markeert. De matrix die het product van Matrix A en Matrix B vertegenwoordigt, heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. U kunt lege vakken tekenen om het aantal rijen en kolommen in deze matrix aan te geven.
2 Markeer de afmetingen van het matrixproduct. Maak een nieuwe lege matrix die de afmetingen van het matrixproduct, het product van de twee matrices, markeert. De matrix die het product van Matrix A en Matrix B vertegenwoordigt, heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. U kunt lege vakken tekenen om het aantal rijen en kolommen in deze matrix aan te geven. - Matrix A heeft 2 rijen, dus het matrixproduct heeft 2 rijen.
- Matrix B heeft 2 kolommen, dus het matrixproduct heeft 2 kolommen.
- Het matrixproduct heeft 2 rijen en 2 kolommen.
-
 3 Zoek het eerste puntproduct. Om een puntproduct te vinden, moet u het eerste element in de eerste rij vermenigvuldigen met het eerste element van de eerste kolom, het tweede element van de eerste rij met het tweede element van de eerste kolom en het derde element in de eerste rij door het derde element in de eerste kolom. Voeg vervolgens hun producten toe om het te vinden punt product. Laten we zeggen dat je hebt besloten om op te lossen voor het element in de 2nd rij en 2nd kolom (rechtsonder) van het matrixproduct eerst. Hier is hoe je het doet:
3 Zoek het eerste puntproduct. Om een puntproduct te vinden, moet u het eerste element in de eerste rij vermenigvuldigen met het eerste element van de eerste kolom, het tweede element van de eerste rij met het tweede element van de eerste kolom en het derde element in de eerste rij door het derde element in de eerste kolom. Voeg vervolgens hun producten toe om het te vinden punt product. Laten we zeggen dat je hebt besloten om op te lossen voor het element in de 2nd rij en 2nd kolom (rechtsonder) van het matrixproduct eerst. Hier is hoe je het doet: - 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
- Het puntproduct is -34 en het hoort rechts onderaan het matrixproduct.
- Wanneer u matrices vermenigvuldigt, gaat het puntproduct in de positie van de rij van de eerste matrix en de kolom van de tweede matrix. Als u bijvoorbeeld het puntproduct van de onderste rij van matrix A en de rechterkolom van matrix B hebt gevonden, is het antwoord, -34, in de onderste rij en rechter kolom van het matrixproduct terechtgekomen.
-
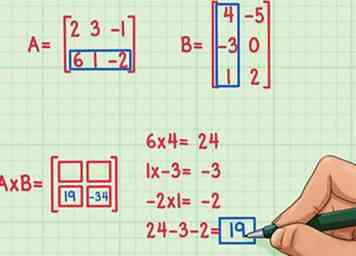 4 Zoek het tweede puntproduct. Stel dat u de term links onderaan het matrixproduct wilt vinden. Om deze term te vinden, hoeft u alleen maar de elementen in de onderste rij van de eerste matrix te vermenigvuldigen met de elementen in de eerste kolom van de tweede matrix en ze vervolgens op te tellen. Gebruik dezelfde methode die u hebt gebruikt om de eerste rij en kolom te vermenigvuldigen - zoek de punt product nog een keer.
4 Zoek het tweede puntproduct. Stel dat u de term links onderaan het matrixproduct wilt vinden. Om deze term te vinden, hoeft u alleen maar de elementen in de onderste rij van de eerste matrix te vermenigvuldigen met de elementen in de eerste kolom van de tweede matrix en ze vervolgens op te tellen. Gebruik dezelfde methode die u hebt gebruikt om de eerste rij en kolom te vermenigvuldigen - zoek de punt product nog een keer. - 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Het puntproduct is -19 en het hoort links onderaan het matrixproduct.
-
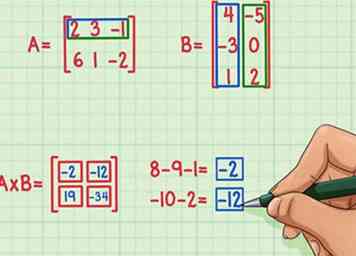 5 Zoek de resterende producten met twee stippen. Als u de term linksboven in het matrixproduct wilt vinden, begint u met het vinden van het puntproduct van de bovenste rij van matrix A en de linkerkolom van matrix B. Hier ziet u hoe u het doet:
5 Zoek de resterende producten met twee stippen. Als u de term linksboven in het matrixproduct wilt vinden, begint u met het vinden van het puntproduct van de bovenste rij van matrix A en de linkerkolom van matrix B. Hier ziet u hoe u het doet: - 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
- Het puntproduct is -2 en het hoort bovenaan links van het matrixproduct.
- Als u de term in de rechterbovenhoek van het matrixproduct wilt vinden, vindt u het puntproduct van de bovenste rij van matrix A en de rechterkolom van matrix B. Hier ziet u hoe u het doet:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Het puntproduct is -12 en het hoort in de rechterbovenhoek van het matrixproduct.
-
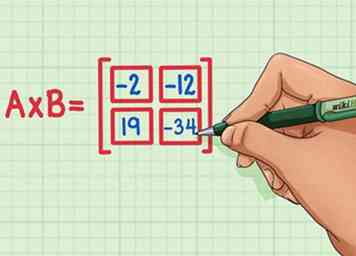 6 Controleer of alle vier de puntproducten zich op de juiste locatie in het matrixproduct bevinden. 19 moet linksonder staan, -34 moet rechtsonder staan, -2 moet linksboven staan en -12 moet rechtsboven staan.
6 Controleer of alle vier de puntproducten zich op de juiste locatie in het matrixproduct bevinden. 19 moet linksonder staan, -34 moet rechtsonder staan, -2 moet linksboven staan en -12 moet rechtsboven staan.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Controleer of de matrices kunnen worden vermenigvuldigd. U kunt matrices alleen vermenigvuldigen als het aantal kolommen van de eerste matrix gelijk is aan het aantal rijen in de tweede matrix.
1 Controleer of de matrices kunnen worden vermenigvuldigd. U kunt matrices alleen vermenigvuldigen als het aantal kolommen van de eerste matrix gelijk is aan het aantal rijen in de tweede matrix. 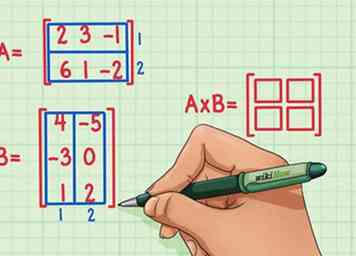 2 Markeer de afmetingen van het matrixproduct. Maak een nieuwe lege matrix die de afmetingen van het matrixproduct, het product van de twee matrices, markeert. De matrix die het product van Matrix A en Matrix B vertegenwoordigt, heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. U kunt lege vakken tekenen om het aantal rijen en kolommen in deze matrix aan te geven.
2 Markeer de afmetingen van het matrixproduct. Maak een nieuwe lege matrix die de afmetingen van het matrixproduct, het product van de twee matrices, markeert. De matrix die het product van Matrix A en Matrix B vertegenwoordigt, heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. U kunt lege vakken tekenen om het aantal rijen en kolommen in deze matrix aan te geven.  3 Zoek het eerste puntproduct. Om een puntproduct te vinden, moet u het eerste element in de eerste rij vermenigvuldigen met het eerste element van de eerste kolom, het tweede element van de eerste rij met het tweede element van de eerste kolom en het derde element in de eerste rij door het derde element in de eerste kolom. Voeg vervolgens hun producten toe om het te vinden punt product. Laten we zeggen dat je hebt besloten om op te lossen voor het element in de 2nd rij en 2nd kolom (rechtsonder) van het matrixproduct eerst. Hier is hoe je het doet:
3 Zoek het eerste puntproduct. Om een puntproduct te vinden, moet u het eerste element in de eerste rij vermenigvuldigen met het eerste element van de eerste kolom, het tweede element van de eerste rij met het tweede element van de eerste kolom en het derde element in de eerste rij door het derde element in de eerste kolom. Voeg vervolgens hun producten toe om het te vinden punt product. Laten we zeggen dat je hebt besloten om op te lossen voor het element in de 2nd rij en 2nd kolom (rechtsonder) van het matrixproduct eerst. Hier is hoe je het doet:  4 Zoek het tweede puntproduct. Stel dat u de term links onderaan het matrixproduct wilt vinden. Om deze term te vinden, hoeft u alleen maar de elementen in de onderste rij van de eerste matrix te vermenigvuldigen met de elementen in de eerste kolom van de tweede matrix en ze vervolgens op te tellen. Gebruik dezelfde methode die u hebt gebruikt om de eerste rij en kolom te vermenigvuldigen - zoek de punt product nog een keer.
4 Zoek het tweede puntproduct. Stel dat u de term links onderaan het matrixproduct wilt vinden. Om deze term te vinden, hoeft u alleen maar de elementen in de onderste rij van de eerste matrix te vermenigvuldigen met de elementen in de eerste kolom van de tweede matrix en ze vervolgens op te tellen. Gebruik dezelfde methode die u hebt gebruikt om de eerste rij en kolom te vermenigvuldigen - zoek de punt product nog een keer.  5 Zoek de resterende producten met twee stippen. Als u de term linksboven in het matrixproduct wilt vinden, begint u met het vinden van het puntproduct van de bovenste rij van matrix A en de linkerkolom van matrix B. Hier ziet u hoe u het doet:
5 Zoek de resterende producten met twee stippen. Als u de term linksboven in het matrixproduct wilt vinden, begint u met het vinden van het puntproduct van de bovenste rij van matrix A en de linkerkolom van matrix B. Hier ziet u hoe u het doet:  6 Controleer of alle vier de puntproducten zich op de juiste locatie in het matrixproduct bevinden. 19 moet linksonder staan, -34 moet rechtsonder staan, -2 moet linksboven staan en -12 moet rechtsboven staan.
6 Controleer of alle vier de puntproducten zich op de juiste locatie in het matrixproduct bevinden. 19 moet linksonder staan, -34 moet rechtsonder staan, -2 moet linksboven staan en -12 moet rechtsboven staan.