Algebra is een tak van de wiskunde die getallen bestudeert door onbekende grootheden te representeren met lettervariabelen, evenals de wiskundige bewerkingen die daarop worden toegepast. Het is de toegangspoort voor studenten tot hogere wiskunde en is al te vaak een struikelblok voor hen, niet alleen in termen van school, maar ook in termen van het kunnen instappen in een goed college en studeren voor hun gewenste carrière. Het belang en de druk van algebra, en wiskunde in het algemeen, motiveren veel ouders om manieren te vinden om hun kinderen te helpen zich voor te bereiden op algebra, niet altijd met een goed begrip van de vaardigheden die hun kinderen zouden moeten beheersen om klaar te zijn voor algebra.

Methode één van de twee:
Het bepalen van de gereedheid van uw kind voor algebra

  1. 1 Overweeg de leeftijd van uw kind. Sommige onderwijskundige onderzoekers, zoals Dr. Herman Epstein, geloven dat het menselijk brein perioden kent van snelle ontwikkeling en perioden waarin weinig ontwikkeling plaatsvindt, waarvan er een samenvalt met een fysieke groeispurt in de leeftijd van 14 tot 17, de middelbare schooljaren.
  2. 2 Overweeg het volwassenheidsniveau van uw kind. Uw kind moet algemene probleemoplossende vaardigheden vertonen, conclusies kunnen trekken uit logisch redeneren en projecten kunnen organiseren.
  3. 3 Let op het wiskundecurriculum in het schooldistrict van uw kind. Historisch gezien werd op Amerikaanse scholen algebra geïntroduceerd in de 9e of 10e klas. Vanwege de politieke druk die gedeeltelijk voortvloeit uit de No Child Left Behind Act, hebben veel schooldistricten de algebra formeel geïntroduceerd in de 8e klas, met voorlopige concepten die in de 7e klas worden onderwezen.
    • Als u uw kind homeschoolt, bekijk dan de curricula uit verschillende districten in uw directe omgeving voor een betere behandeling wanneer het een geschikt moment is om uw kind voor te bereiden op algebra.
  4. 4 Beoordeel de bereidheid van uw kind voor algebra. U kunt dit op 1 of 2 manieren doen:
    • Via een formele algebra gereedheidstest. Veel schooldistricten bieden algebra-bereidheidstests aan als middel om studenten in studietrajecten te plaatsen voor hun middelbare schooltijd. Deze tests worden meestal aangeboden tijdens de middelbare schooljaren van een student. Organisaties zoals College Preparatory Mathematics en Sylvan Learning bieden online of downloadbare algebra gereedheidstests.
    • Door regelmatig het wiskundehuiswerk van je kind te bekijken. Gebruik de informatie die wordt gepresenteerd onder 'Vereisten voor Algebra', samen met een goed begrip van het leerplan van uw schooldistrict om de voortgang van uw kind bij het ontwikkelen van de voorlopige vaardigheden voor het leren van de algebra te volgen.
  5. 5 Introduceer algebraïsche concepten voor uw kind. Veel van de concepten die in de algebra worden onderwezen, kunnen op een jongere leeftijd aan kinderen worden gepresenteerd als ze op een manier worden gedaan die past bij hun leeftijd. U kunt bijvoorbeeld het begrip variabelen introduceren door uw kind te vragen welk nummer is toegevoegd aan 6 merken 10.

Methode twee van twee:
Vereisten voor Algebra

  1. 1 Begrijp en schrijf verschillende nummervormen. Uw kind moet tussen de volgende formulieren kunnen lezen, schrijven, vergelijken en converteren:
    • Gehele getallen. Gehele getallen omvatten getallen (1, 2, 3, enz., Die positieve gehele getallen zijn), gehele getallen (0, 1, 2, 3, etc.) en hun tegenhangers met negatieve waarden (additief invers, -1, -2, -3, etc.).
    • Breuken. Breuken worden geschreven als één getal (de teller) boven een andere (de noemer), gescheiden door een lijn, zoals 1/2. Uw kind moet de juiste breuken begrijpen (die een teller hebben die kleiner is dan de noemer, zoals 2/3), onjuiste breuken (die een teller hebben die groter of groter is dan de noemer, zoals 3/2) en gemengde cijfers (die een geheel getal combineren met een breuk, zoals 1 1/2).
    • Decimalen. Decimalen zijn een andere manier om fractionele waarden uit te drukken met een decimaal in plaats van een breukstreep. Uw kind moet de waarde van de decimale plaats kunnen begrijpen (0,5 is groter dan 0,05 omdat 5 tienden meer dan 5 honderdsten is) en decimalen in breuken kunnen omzetten en omgekeerd.
    • Procenten. Percents zijn een uitdrukking van numerieke waarden als delen van 100 ("percent"). Uw kind moet in staat zijn om voor hetzelfde getal tussen procentuele en decimale waarden te converteren.
    • Exponenten. Exponenten zijn superscript (verhoogde) getallen die worden gebruikt om aan te geven hoe vaak een basegetal wordt gebruikt als factor bij vermenigvuldiging. Ze worden soms 'krachten' genoemd. Exponenten kunnen ook worden geschreven als normale cijfers na een cursor (^) wanneer superscripting niet mogelijk is. Uw kind moet getallen die zijn verhoogd naar bevoegdheden kunnen converteren naar hun equivalente waarden, zoals 4 ^ 2 = 16 en 10 ^ 3 = 1000.
    • Wetenschappelijke notatie. Wetenschappelijke notatie schrijft een grote numerieke waarde als een decimaal vermenigvuldigd met 10 verhoogd tot een macht. Het aantal 1.600.000 zou in wetenschappelijke notatie worden geschreven als 1.6 x 10 ^ 6.
  2. 2 Bereken cijfers in alle hierboven beschreven vormen. Uw kind moet gehele getallen, breuken, decimalen, procenten en in wetenschappelijke notatie kunnen toevoegen, aftrekken, vermenigvuldigen en delen, met enkele van de volgende gerelateerde vaardigheden:
    • Bij het optellen of aftrekken van breuken moet uw kind in staat zijn breuken in equivalente vormen om te zetten, zodat beide termen dezelfde noemer hebben. Bij het vermenigvuldigen van breuken moet uw kind in staat zijn de tellers samen en de noemers bij elkaar te vermenigvuldigen en het resultaat tot de laagste termen te reduceren.
    • Bij het vermenigvuldigen van decimalen samen, moet uw kind de decimale punt correct in het product kunnen plaatsen. Wanneer de ene decimaal door een andere wordt gedeeld, moet uw kind in staat zijn om de decimale punt correct in het quotiënt te plaatsen door de decimale punten in het dividend en de deler hetzelfde aantal plaatsen naar rechts te verplaatsen om van de deler een geheel getal te maken.
  3. 3 Factornummers kunnen zijn. Factoring is het vermogen om een ​​nummer te identificeren als het product van 2 of meer kleinere getallen (factoren). Uw kind moet in staat zijn om factoren voor een bepaald aantal te identificeren en priemgetallen te identificeren, die alleen deelbaar zijn door 1 en zichzelf. Bovendien moet uw kind het volgende kunnen begrijpen en uitvoeren:
    • De grootste gemeenschappelijke factor (GCF). Dit is het grootste aantal dat gelijk verdeeld kan worden in 2 of meer verschillende nummers; bijvoorbeeld, de grootste gemeenschappelijke factor van 12 en 20 is 4 (3 x 4 = 12, 5 x 4 = 20).
    • Minst (of laagste) veelvoud (LCM). Dit is het kleinste getal dat een veelvoud is van 2 of meer verschillende nummers; het kleinste gemene veelvoud van 6 en 9 is bijvoorbeeld 18 (3 x 6 = 18, 2 x 9 = 18).
    • Prime factoring. Dit is het kunnen uitdrukken van een gegeven getal als een product van priemgetallen. De primaire factoring van 60 is bijvoorbeeld 2 x 2 x 3 x 5.
  4. 4 Informatie over verhoudingen, verhoudingen en tarieven. "Ratio" is de vergelijking van 2 hoeveelheden met elkaar, terwijl "verhouding" verwijst naar de hoeveelheid van een item tegen een geheel. In een kom fruit met 3 appels en 5 sinaasappelen is de verhouding van appels tot sinaasappels 3: 5 (ook beschrijfbaar als 3/5), terwijl het aandeel appels tot alle vruchten 3: 8 (of 3/8) is. "Snelheid" is een verhouding van 2 metingen, meestal van verschillende typen, zoals mijlen per uur, hartslagen per minuut of cycli per seconde.
    • Gerelateerd aan verhoudingen en verhoudingen zijn de concepten van kansen en kansen. Waarschijnlijkheid is een verhouding van het gewenste resultaat tot alle mogelijke uitkomsten; de kans om koppen te krijgen op een muntflip is 1: 2 (1/2), omdat een muntstuk ofwel kop of munt kan oplopen. "Kansen" is de verhouding tussen het gewenste resultaat en ongewenste resultaten; de kans om koppen te krijgen op een toss is 1: 1.
  5. 5 Identificeer en teken verschillende geometrische vormen. Deze vaardigheden zijn iets meer een voorwaarde voor meetkundeklassen dan voor algebra, maar ze hebben betrekking op het vermogen om patronen te herkennen in getallenreeksen en andere gebieden.
  6. 6 Meet en bereken de afmetingen en eigenschappen van verschillende geometrische vormen. Uw kind moet in staat zijn om een ​​liniaal, kompas en gradenboog te gebruiken en moet het volgende kunnen vinden:
    • Perimeter: de totale lengte van alle randen van een 2-dimensionaal object.
    • Gebied: de hoeveelheid ruimte die een tweedimensionaal object in beslag neemt.
    • Volume: de hoeveelheid ruimte die een driedimensionaal object in beslag neemt.
    • Oppervlakte: het totale oppervlak van elk oppervlak van een driedimensionaal object.
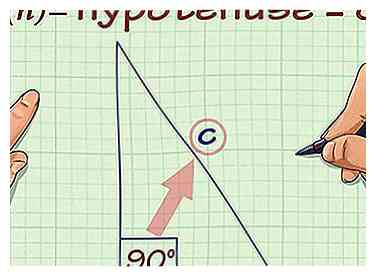  7. 7 Werk met de stelling van Pythagoras. De stelling van Pythagoras stelt dat het kwadraat van de lengte van de hypotenusa van een rechthoekige driehoek (de zijde tegenover de rechte hoek) gelijk is aan de som van de vierkanten van de lengte van de andere twee zijden. Deze vaardigheid helpt je kind voor te bereiden, niet alleen voor algebra en geometrie, maar ook trigonometrie. Uw kind moet deze relatie kunnen gebruiken om de lengte van elke zijde van een rechthoekige driehoek te vinden wanneer de andere 2 lengten bekend zijn en ook aangeven of een driehoek een rechthoekige driehoek is als de lengte van alle 3 zijden wordt gegeven.
    • Omdat het berekenen van de lengte van een onbekende zijde vierkante wortels vereist, is dit een mogelijkheid voor uw kind om vaardigheden te ontwikkelen met behulp van een rekenmachine.
  8. 8 Verzamel, organiseer en presenteer informatie zodat anderen het kunnen begrijpen. Uw kind moet een rudimentair inzicht hebben in statistieken (gemiddelde, mediaan, modus en bereik) en in staat zijn om staafdiagrammen, lijngrafieken en cirkeldiagrammen te lezen en te maken, evenals punten op een tweedimensionaal raster te kunnen plotten .
  9. 9 Patronen begrijpen en analyseren. Patronen met constante veranderingsbereiken (zoals 2, 4, 6, 8, etc.) hebben betrekking op zowel algebra als geometrie. Uw kind moet in staat zijn de aard van een patroon te herkennen en te projecteren wat het volgende getal in een numerieke volgorde zal zijn.
  10. 10 Begrijp het concept van variabelen. Variabelen zijn onbekend of variërende grootheden in vergelijkingen die in de algebra per letter worden weergegeven. Dit concept wordt vaak enkele jaren vóór elementaire algebra geïntroduceerd door dozen of spaties te gebruiken om de onbekende hoeveelheden weer te geven. Uw kind moet het begrip variabelen in dit formaat kunnen begrijpen en de waarde van de onbekende hoeveelheid kunnen vinden.
  11. 11 Vertegenwoordig wiskundige functies als vergelijkingen en op grafieken. Een functie is de relatie tussen een ingangsnummer en een enkel, resulterend uitgangsnummer. (Als een functie werd gedefinieerd als het toevoegen van 7 aan elk getal, zou 1 een invoer zijn en 8 de bijbehorende uitvoer.) Uw kind moet het uitvoernummer voor een bepaald invoernummer en de functie kunnen berekenen, een tabel met invoer en uitvoer kunnen opbouwen waarden voor een bepaalde functie en construeer een lijngrafiek uit een tabel met invoer- en uitvoerwaarden.