Een fundamenteel onderdeel van het leren van de algebra is het leren hoe het omgekeerde van een functie te vinden, of f (x). De inverse van een functie wordt aangeduid met f ^ -1 (x) en wordt visueel weergegeven als de oorspronkelijke functie die wordt gereflecteerd over de lijn y = x. Dit artikel laat zien hoe je de inverse van een functie kunt vinden.
Stappen
-
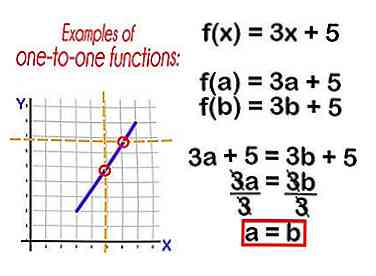 1 Zorg ervoor dat uw functie één-op-één is. Alleen een-op-een-functies hebben inversie.
1 Zorg ervoor dat uw functie één-op-één is. Alleen een-op-een-functies hebben inversie. - Een functie is één-op-één als deze de verticale-lijntest en de horizontale-lijntest doorstaat. Teken een verticale lijn door de hele grafiek van de functie en tel het aantal keren dat de lijn de functie raakt. Teken vervolgens een horizontale lijn door de hele grafiek van de functie en tel het aantal keren dat deze lijn de functie raakt. Als elke regel slechts één keer de functie raakt, is de functie één-op-één.
- Als een grafiek de verticale lijntest niet doorstaat, is dit geen functie.
- Om algebraïsch te bepalen of de functie één-op-één is, plug je f (a) en f (b) in je functie en kijk je of a = b. Laten we als voorbeeld f (x) = 3x + 5 nemen.
- f (a) = 3a + 5; f (b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Dus, f (x) is één-op-één.
- Een functie is één-op-één als deze de verticale-lijntest en de horizontale-lijntest doorstaat. Teken een verticale lijn door de hele grafiek van de functie en tel het aantal keren dat de lijn de functie raakt. Teken vervolgens een horizontale lijn door de hele grafiek van de functie en tel het aantal keren dat deze lijn de functie raakt. Als elke regel slechts één keer de functie raakt, is de functie één-op-één.
-
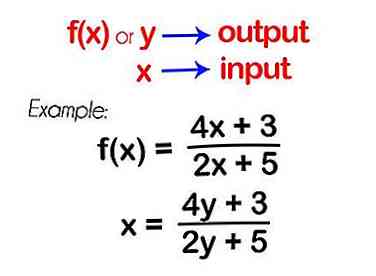 2 Gegeven een functie, wissel je de x's en de y's. Onthoud dat f (x) een vervanging is voor 'y'.
2 Gegeven een functie, wissel je de x's en de y's. Onthoud dat f (x) een vervanging is voor 'y'. - In een functie staat "f (x)" of "y" voor de uitvoer en "x" voor de invoer. Om de inverse van een functie te vinden, schakelt u de ingangen en de uitgangen.
- Voorbeeld: Laten we f (x) = (4x + 3) / (2x + 5) nemen - dat is één-op-één. Door de x's en y's te veranderen, krijgen we x = (4y + 3) / (2y + 5).
-
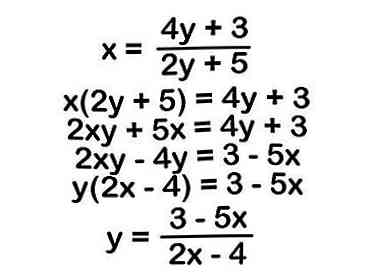 3 Los op voor de nieuwe "y."U moet de expressies manipuleren om op te lossen voor y, of om de nieuwe bewerkingen te vinden die moeten worden uitgevoerd op de invoer om de inverse als een uitvoer te verkrijgen.
3 Los op voor de nieuwe "y."U moet de expressies manipuleren om op te lossen voor y, of om de nieuwe bewerkingen te vinden die moeten worden uitgevoerd op de invoer om de inverse als een uitvoer te verkrijgen. - Dit kan lastig zijn, afhankelijk van je expressie. Mogelijk moet je algebraïsche trucs gebruiken zoals cross-vermenigvuldiging of factoring om de uitdrukking te evalueren en te vereenvoudigen.
- In ons voorbeeld nemen we de volgende stappen om y te isoleren:
- We beginnen met x = (4y + 3) / (2y + 5)
- x (2y + 5) = 4y + 3 - vermenigvuldig beide zijden met (2y + 5)
- 2xy + 5x = 4y + 3 - Verdeel de x's
- 2xy - 4y = 3 - 5x - Haal alle y-termen op één kant op
- y (2x - 4) = 3 - 5x - Omgekeerd distribueren om de y-termen te consolideren
- y = (3 - 5x) / (2x - 4) - Verdelen om uw antwoord te krijgen
-
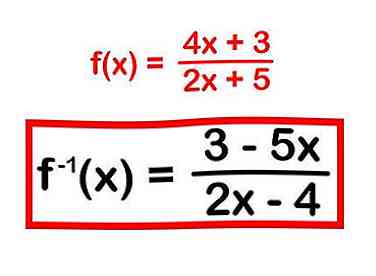 4 Vervang de nieuwe "y" door f ^ -1 (x). Dit is de vergelijking voor de inverse van uw oorspronkelijke functie.
4 Vervang de nieuwe "y" door f ^ -1 (x). Dit is de vergelijking voor de inverse van uw oorspronkelijke functie. - Ons laatste antwoord is f ^ -1 (x) = (3 - 5x) / (2x - 4). Dit is de inverse van f (x) = (4x + 3) / (2x + 5).
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Zorg ervoor dat uw functie één-op-één is. Alleen een-op-een-functies hebben inversie.
1 Zorg ervoor dat uw functie één-op-één is. Alleen een-op-een-functies hebben inversie. 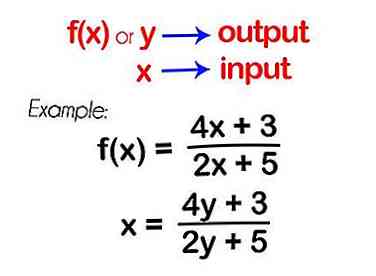 2 Gegeven een functie, wissel je de x's en de y's. Onthoud dat f (x) een vervanging is voor 'y'.
2 Gegeven een functie, wissel je de x's en de y's. Onthoud dat f (x) een vervanging is voor 'y'. 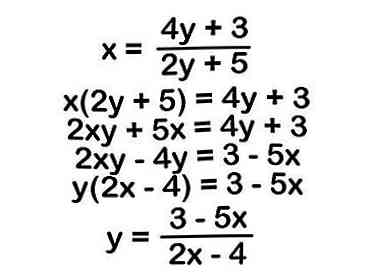 3 Los op voor de nieuwe "y."U moet de expressies manipuleren om op te lossen voor y, of om de nieuwe bewerkingen te vinden die moeten worden uitgevoerd op de invoer om de inverse als een uitvoer te verkrijgen.
3 Los op voor de nieuwe "y."U moet de expressies manipuleren om op te lossen voor y, of om de nieuwe bewerkingen te vinden die moeten worden uitgevoerd op de invoer om de inverse als een uitvoer te verkrijgen. 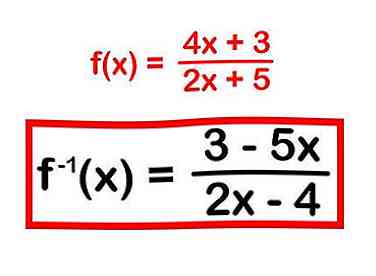 4 Vervang de nieuwe "y" door f ^ -1 (x). Dit is de vergelijking voor de inverse van uw oorspronkelijke functie.
4 Vervang de nieuwe "y" door f ^ -1 (x). Dit is de vergelijking voor de inverse van uw oorspronkelijke functie.