Polynomiaal betekent "veel termen" en het kan verwijzen naar een verscheidenheid aan uitdrukkingen die constanten, variabelen en exponenten kunnen omvatten. Bijvoorbeeld, x - 2 is een polynoom; zo is het 25. Om de graad van een polynoom te vinden, hoeft u alleen de grootste exponent in de polynoom te vinden.[1] Als u de mate van een polynoom in verschillende situaties wilt vinden, volgt u deze stappen.
Deel een van de drie:
Polynomen met één variabele of minder
-
 1 Combineer dezelfde termen. Combineer alle gelijke termen in de uitdrukking zodat u het kunt vereenvoudigen, als ze al niet zijn gecombineerd. Laten we zeggen dat je met de volgende expressie werkt: 3x2 - 3x4 - 5 + 2x + 2x2 - x. Combineer gewoon alle x2, x, en constante termen van de expressie om 5x te krijgen2 - 3x4 - 5 + x.
1 Combineer dezelfde termen. Combineer alle gelijke termen in de uitdrukking zodat u het kunt vereenvoudigen, als ze al niet zijn gecombineerd. Laten we zeggen dat je met de volgende expressie werkt: 3x2 - 3x4 - 5 + 2x + 2x2 - x. Combineer gewoon alle x2, x, en constante termen van de expressie om 5x te krijgen2 - 3x4 - 5 + x. -
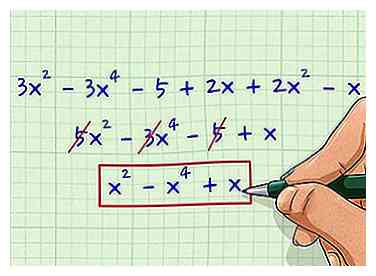 2 Laat alle constanten en coëfficiënten vallen. De constante termen zijn alle termen die niet aan een variabele zijn gekoppeld, zoals 3 of 5. De coëfficiënten zijn de termen die zijn gekoppeld aan de variabele. Wanneer u op zoek bent naar de mate van een veelterm, kunt u deze voorwaarden negeren of deze gewoon negeren. Bijvoorbeeld, de coëfficiënt van de term 5x2 zou 5 zijn. De mate is onafhankelijk van de coëfficiënten, dus je hebt ze niet nodig.
2 Laat alle constanten en coëfficiënten vallen. De constante termen zijn alle termen die niet aan een variabele zijn gekoppeld, zoals 3 of 5. De coëfficiënten zijn de termen die zijn gekoppeld aan de variabele. Wanneer u op zoek bent naar de mate van een veelterm, kunt u deze voorwaarden negeren of deze gewoon negeren. Bijvoorbeeld, de coëfficiënt van de term 5x2 zou 5 zijn. De mate is onafhankelijk van de coëfficiënten, dus je hebt ze niet nodig. - Werken met de vergelijking 5x2 - 3x4 - 5 + x, je zou de constanten en coëfficiënten laten vallen om x te krijgen2 - x4 + x.
-
 3 Zet de termen in dalende volgorde van hun exponenten. Dit wordt ook wel de polynomiaal genoemd standaard vorm.[2]. De term met de hoogste exponent moet de eerste zijn en de term met de laagste exponent moet de laatste zijn. Hiermee kunt u zien welke term de exponent heeft met de grootste waarde. In het vorige voorbeeld zou u overblijven
3 Zet de termen in dalende volgorde van hun exponenten. Dit wordt ook wel de polynomiaal genoemd standaard vorm.[2]. De term met de hoogste exponent moet de eerste zijn en de term met de laagste exponent moet de laatste zijn. Hiermee kunt u zien welke term de exponent heeft met de grootste waarde. In het vorige voorbeeld zou u overblijven
-X4 + x2 + x. -
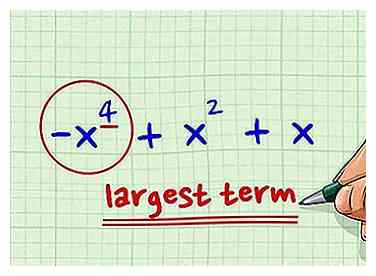 4 Zoek de kracht van de grootste term. De kracht is gewoon nummer in de exponent. In het voorbeeld, -x4 + x2 + x, de kracht van de eerste term is 4. Omdat je de veelterm hebt gerangschikt om de grootste exponent als eerste te plaatsen, zul je daar de grootste term vinden.
4 Zoek de kracht van de grootste term. De kracht is gewoon nummer in de exponent. In het voorbeeld, -x4 + x2 + x, de kracht van de eerste term is 4. Omdat je de veelterm hebt gerangschikt om de grootste exponent als eerste te plaatsen, zul je daar de grootste term vinden. -
 5 Identificeer dit nummer als de graad van het polynoom. Je kunt alleen schrijven dat de graad van de polynoom = 4 is, of je kunt het antwoord in een meer geschikte vorm schrijven: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Je bent helemaal klaar.[3]
5 Identificeer dit nummer als de graad van het polynoom. Je kunt alleen schrijven dat de graad van de polynoom = 4 is, of je kunt het antwoord in een meer geschikte vorm schrijven: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Je bent helemaal klaar.[3] -
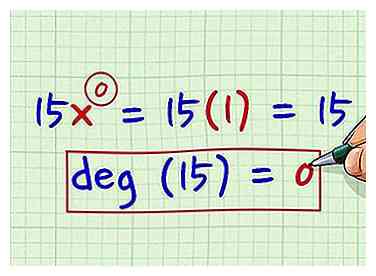 6 Weet dat de graad van een constante nul is. Als je polynoom slechts een constante is, zoals 15 of 55, dan is de graad van die polynoom eigenlijk nul. Je kunt de constante term zien als vastgemaakt aan een variabele in de mate van 0, wat echt 1 is. Als je bijvoorbeeld de constante 15 hebt, kun je het zien als 15x0, wat echt 15 x 1 of 15 is. Dit bewijst dat de graad van een constante 0 is.
6 Weet dat de graad van een constante nul is. Als je polynoom slechts een constante is, zoals 15 of 55, dan is de graad van die polynoom eigenlijk nul. Je kunt de constante term zien als vastgemaakt aan een variabele in de mate van 0, wat echt 1 is. Als je bijvoorbeeld de constante 15 hebt, kun je het zien als 15x0, wat echt 15 x 1 of 15 is. Dit bewijst dat de graad van een constante 0 is.
Tweede deel van de drie:
Polynomen met meerdere variabelen
-
 1 Schrijf de uitdrukking. Het vinden van de graad van een polynoom met meerdere variabelen is alleen een beetje lastiger dan het vinden van de graad van een polynoom met één variabele. Laten we zeggen dat je met de volgende expressie werkt:
1 Schrijf de uitdrukking. Het vinden van de graad van een polynoom met meerdere variabelen is alleen een beetje lastiger dan het vinden van de graad van een polynoom met één variabele. Laten we zeggen dat je met de volgende expressie werkt: - X5Y3z + 2xy3 + 4x2yz2
-
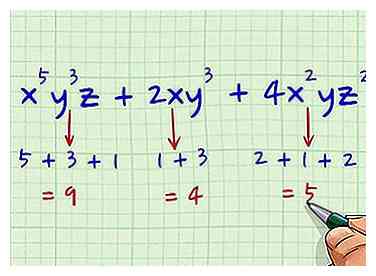 2 Voeg de mate van variabelen in elke term toe. Tel de graden van de variabelen op in elk van de termen; het maakt niet uit dat het andere variabelen zijn. Onthoud dat de graad van een variabele zonder een schriftelijke graad, zoals x of y, er slechts één is. Hier is hoe je het doet voor alle drie de termen:[4]
2 Voeg de mate van variabelen in elke term toe. Tel de graden van de variabelen op in elk van de termen; het maakt niet uit dat het andere variabelen zijn. Onthoud dat de graad van een variabele zonder een schriftelijke graad, zoals x of y, er slechts één is. Hier is hoe je het doet voor alle drie de termen:[4] - X5Y3z = 5 + 3 + 1 = 9
- 2xy3 = 1 + 3 = 4
- 4x2yz2 = 2 + 1 + 2 = 5
-
 3 Identificeer de grootste mate van deze voorwaarden. De grootste van deze drie termen is 9, de waarde van de toegevoegde graadwaarden van de eerste term.
3 Identificeer de grootste mate van deze voorwaarden. De grootste van deze drie termen is 9, de waarde van de toegevoegde graadwaarden van de eerste term. -
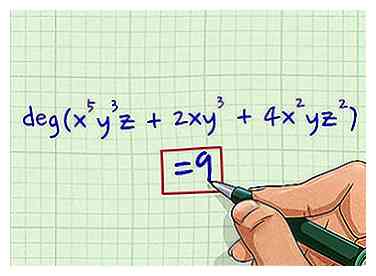 4 Identificeer dit nummer als de graad van het polynoom. 9 is de graad van het gehele polynoom. U kunt het definitieve antwoord als volgt schrijven: graden (x5Y3z + 2xy3 + 4x2yz2) = 9.
4 Identificeer dit nummer als de graad van het polynoom. 9 is de graad van het gehele polynoom. U kunt het definitieve antwoord als volgt schrijven: graden (x5Y3z + 2xy3 + 4x2yz2) = 9.
Derde deel van de drie:
Rationele uitdrukkingen
-
 1 Noteer de uitdrukking. Stel dat u met de volgende expressie werkt: (x2 + 1) / (6x -2).[5]
1 Noteer de uitdrukking. Stel dat u met de volgende expressie werkt: (x2 + 1) / (6x -2).[5] -
 2 Elimineer alle coëfficiënten en constanten. U hebt de coëfficiënten of constante termen niet nodig om de graad van een polynoom met breuken te vinden. Dus, elimineer de 1 van de teller en de 6 en -2 van de noemer. Je blijft zitten met x2/X.
2 Elimineer alle coëfficiënten en constanten. U hebt de coëfficiënten of constante termen niet nodig om de graad van een polynoom met breuken te vinden. Dus, elimineer de 1 van de teller en de 6 en -2 van de noemer. Je blijft zitten met x2/X. -
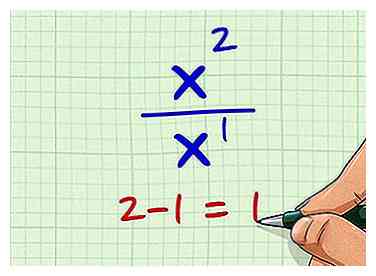 3 Trek de mate van de variabele in de noemer af van de graad van de variabele in de teller. De graad van de variabele in de teller is 2 en de graad van de variabele in de noemer is 1. Dus, trek 1 van 2 af. 2-1 = 1.
3 Trek de mate van de variabele in de noemer af van de graad van de variabele in de teller. De graad van de variabele in de teller is 2 en de graad van de variabele in de noemer is 1. Dus, trek 1 van 2 af. 2-1 = 1. -
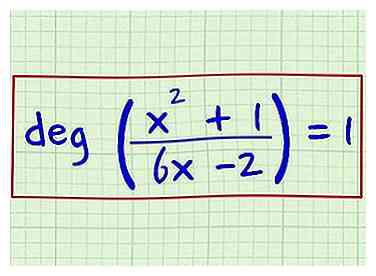 4 Schrijf het resultaat als uw antwoord. De mate van deze rationele expressie is 1. Je kunt het zo schrijven: graden [(x2 + 1) / (6x -2)] = 1.
4 Schrijf het resultaat als uw antwoord. De mate van deze rationele expressie is 1. Je kunt het zo schrijven: graden [(x2 + 1) / (6x -2)] = 1.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Combineer dezelfde termen. Combineer alle gelijke termen in de uitdrukking zodat u het kunt vereenvoudigen, als ze al niet zijn gecombineerd. Laten we zeggen dat je met de volgende expressie werkt: 3x2 - 3x4 - 5 + 2x + 2x2 - x. Combineer gewoon alle x2, x, en constante termen van de expressie om 5x te krijgen2 - 3x4 - 5 + x.
1 Combineer dezelfde termen. Combineer alle gelijke termen in de uitdrukking zodat u het kunt vereenvoudigen, als ze al niet zijn gecombineerd. Laten we zeggen dat je met de volgende expressie werkt: 3x2 - 3x4 - 5 + 2x + 2x2 - x. Combineer gewoon alle x2, x, en constante termen van de expressie om 5x te krijgen2 - 3x4 - 5 + x. 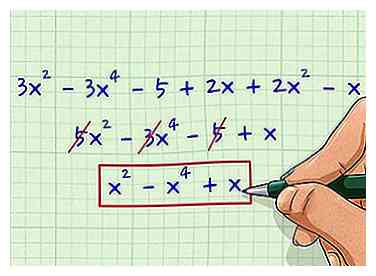 2 Laat alle constanten en coëfficiënten vallen. De constante termen zijn alle termen die niet aan een variabele zijn gekoppeld, zoals 3 of 5. De coëfficiënten zijn de termen die zijn gekoppeld aan de variabele. Wanneer u op zoek bent naar de mate van een veelterm, kunt u deze voorwaarden negeren of deze gewoon negeren. Bijvoorbeeld, de coëfficiënt van de term 5x2 zou 5 zijn. De mate is onafhankelijk van de coëfficiënten, dus je hebt ze niet nodig.
2 Laat alle constanten en coëfficiënten vallen. De constante termen zijn alle termen die niet aan een variabele zijn gekoppeld, zoals 3 of 5. De coëfficiënten zijn de termen die zijn gekoppeld aan de variabele. Wanneer u op zoek bent naar de mate van een veelterm, kunt u deze voorwaarden negeren of deze gewoon negeren. Bijvoorbeeld, de coëfficiënt van de term 5x2 zou 5 zijn. De mate is onafhankelijk van de coëfficiënten, dus je hebt ze niet nodig.  3 Zet de termen in dalende volgorde van hun exponenten. Dit wordt ook wel de polynomiaal genoemd standaard vorm.[2]. De term met de hoogste exponent moet de eerste zijn en de term met de laagste exponent moet de laatste zijn. Hiermee kunt u zien welke term de exponent heeft met de grootste waarde. In het vorige voorbeeld zou u overblijven
3 Zet de termen in dalende volgorde van hun exponenten. Dit wordt ook wel de polynomiaal genoemd standaard vorm.[2]. De term met de hoogste exponent moet de eerste zijn en de term met de laagste exponent moet de laatste zijn. Hiermee kunt u zien welke term de exponent heeft met de grootste waarde. In het vorige voorbeeld zou u overblijven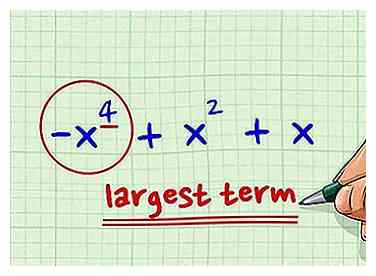 4 Zoek de kracht van de grootste term. De kracht is gewoon nummer in de exponent. In het voorbeeld, -x4 + x2 + x, de kracht van de eerste term is 4. Omdat je de veelterm hebt gerangschikt om de grootste exponent als eerste te plaatsen, zul je daar de grootste term vinden.
4 Zoek de kracht van de grootste term. De kracht is gewoon nummer in de exponent. In het voorbeeld, -x4 + x2 + x, de kracht van de eerste term is 4. Omdat je de veelterm hebt gerangschikt om de grootste exponent als eerste te plaatsen, zul je daar de grootste term vinden.  5 Identificeer dit nummer als de graad van het polynoom. Je kunt alleen schrijven dat de graad van de polynoom = 4 is, of je kunt het antwoord in een meer geschikte vorm schrijven: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Je bent helemaal klaar.[3]
5 Identificeer dit nummer als de graad van het polynoom. Je kunt alleen schrijven dat de graad van de polynoom = 4 is, of je kunt het antwoord in een meer geschikte vorm schrijven: deg (3x2 - 3x4 - 5 + 2x + 2x2 - x) = 3. Je bent helemaal klaar.[3] 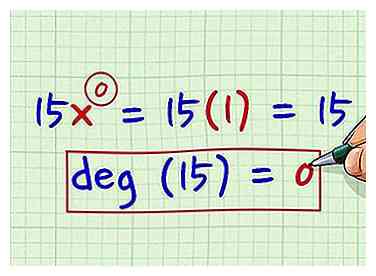 6 Weet dat de graad van een constante nul is. Als je polynoom slechts een constante is, zoals 15 of 55, dan is de graad van die polynoom eigenlijk nul. Je kunt de constante term zien als vastgemaakt aan een variabele in de mate van 0, wat echt 1 is. Als je bijvoorbeeld de constante 15 hebt, kun je het zien als 15x0, wat echt 15 x 1 of 15 is. Dit bewijst dat de graad van een constante 0 is.
6 Weet dat de graad van een constante nul is. Als je polynoom slechts een constante is, zoals 15 of 55, dan is de graad van die polynoom eigenlijk nul. Je kunt de constante term zien als vastgemaakt aan een variabele in de mate van 0, wat echt 1 is. Als je bijvoorbeeld de constante 15 hebt, kun je het zien als 15x0, wat echt 15 x 1 of 15 is. Dit bewijst dat de graad van een constante 0 is.  1 Schrijf de uitdrukking. Het vinden van de graad van een polynoom met meerdere variabelen is alleen een beetje lastiger dan het vinden van de graad van een polynoom met één variabele. Laten we zeggen dat je met de volgende expressie werkt:
1 Schrijf de uitdrukking. Het vinden van de graad van een polynoom met meerdere variabelen is alleen een beetje lastiger dan het vinden van de graad van een polynoom met één variabele. Laten we zeggen dat je met de volgende expressie werkt: 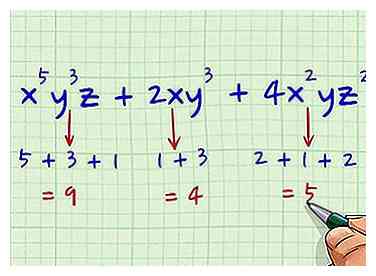 2 Voeg de mate van variabelen in elke term toe. Tel de graden van de variabelen op in elk van de termen; het maakt niet uit dat het andere variabelen zijn. Onthoud dat de graad van een variabele zonder een schriftelijke graad, zoals x of y, er slechts één is. Hier is hoe je het doet voor alle drie de termen:[4]
2 Voeg de mate van variabelen in elke term toe. Tel de graden van de variabelen op in elk van de termen; het maakt niet uit dat het andere variabelen zijn. Onthoud dat de graad van een variabele zonder een schriftelijke graad, zoals x of y, er slechts één is. Hier is hoe je het doet voor alle drie de termen:[4]  3 Identificeer de grootste mate van deze voorwaarden. De grootste van deze drie termen is 9, de waarde van de toegevoegde graadwaarden van de eerste term.
3 Identificeer de grootste mate van deze voorwaarden. De grootste van deze drie termen is 9, de waarde van de toegevoegde graadwaarden van de eerste term. 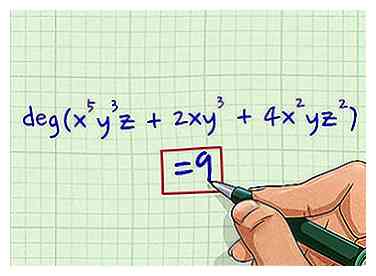 4 Identificeer dit nummer als de graad van het polynoom. 9 is de graad van het gehele polynoom. U kunt het definitieve antwoord als volgt schrijven: graden (x5Y3z + 2xy3 + 4x2yz2) = 9.
4 Identificeer dit nummer als de graad van het polynoom. 9 is de graad van het gehele polynoom. U kunt het definitieve antwoord als volgt schrijven: graden (x5Y3z + 2xy3 + 4x2yz2) = 9.  1 Noteer de uitdrukking. Stel dat u met de volgende expressie werkt: (x2 + 1) / (6x -2).[5]
1 Noteer de uitdrukking. Stel dat u met de volgende expressie werkt: (x2 + 1) / (6x -2).[5]  2 Elimineer alle coëfficiënten en constanten. U hebt de coëfficiënten of constante termen niet nodig om de graad van een polynoom met breuken te vinden. Dus, elimineer de 1 van de teller en de 6 en -2 van de noemer. Je blijft zitten met x2/X.
2 Elimineer alle coëfficiënten en constanten. U hebt de coëfficiënten of constante termen niet nodig om de graad van een polynoom met breuken te vinden. Dus, elimineer de 1 van de teller en de 6 en -2 van de noemer. Je blijft zitten met x2/X. 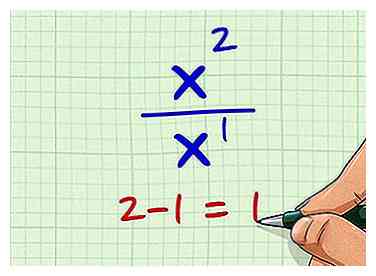 3 Trek de mate van de variabele in de noemer af van de graad van de variabele in de teller. De graad van de variabele in de teller is 2 en de graad van de variabele in de noemer is 1. Dus, trek 1 van 2 af. 2-1 = 1.
3 Trek de mate van de variabele in de noemer af van de graad van de variabele in de teller. De graad van de variabele in de teller is 2 en de graad van de variabele in de noemer is 1. Dus, trek 1 van 2 af. 2-1 = 1. 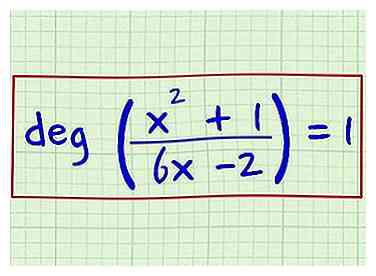 4 Schrijf het resultaat als uw antwoord. De mate van deze rationele expressie is 1. Je kunt het zo schrijven: graden [(x2 + 1) / (6x -2)] = 1.
4 Schrijf het resultaat als uw antwoord. De mate van deze rationele expressie is 1. Je kunt het zo schrijven: graden [(x2 + 1) / (6x -2)] = 1.