De grafiek van een polynoom of functie onthult veel kenmerken die niet duidelijk zouden zijn zonder een visuele representatie. Een van deze kenmerken is de symmetrie-as: een verticale lijn op een grafiek die de grafiek in twee symmetrische spiegelbeelden splitst. Het vinden van de symmetrieas voor een bepaald polynoom is tamelijk eenvoudig. Er zijn twee basismethoden.
Methode één van de twee:
De as van symmetrie voor polynomen vinden met een graad van 2
-
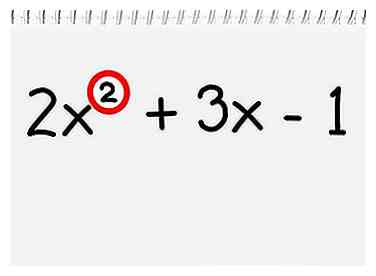 1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas met behulp van deze methode vinden. Gebruik methode 2 als de graad van het polynoom hoger is dan 2.
1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas met behulp van deze methode vinden. Gebruik methode 2 als de graad van het polynoom hoger is dan 2. - Ter illustratie, neem als voorbeeld de veelterm 2x2 + 3x - 1. Deze hoogste aanwezige exponent is de x2, dus het is een polynoom van de 2e orde, en je kunt deze eerste methode gebruiken om de symmetrieas te vinden.
-
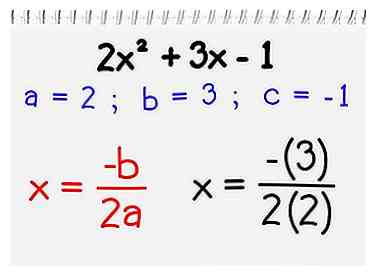 2 Steek uw nummers in de symmetrie-assen-formule. Om de symmetrieas te berekenen voor een 2e-orde polynoom in de formulierbijl2 + bx + c (een parabool), gebruik de basisformule x = -b / 2a.
2 Steek uw nummers in de symmetrie-assen-formule. Om de symmetrieas te berekenen voor een 2e-orde polynoom in de formulierbijl2 + bx + c (een parabool), gebruik de basisformule x = -b / 2a. - In het bovenstaande voorbeeld is a = 2 b = 3 en c = -1. Voeg deze waarden in uw formule in, en u krijgt:
x = -3 / 2 (2) = -3/4.
- In het bovenstaande voorbeeld is a = 2 b = 3 en c = -1. Voeg deze waarden in uw formule in, en u krijgt:
-
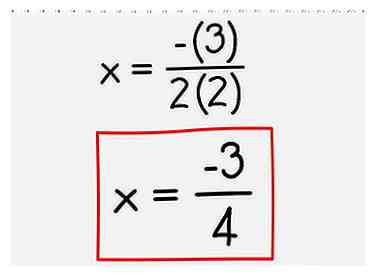 3 Noteer de vergelijking van de symmetrieas. De waarde die u met uw symmetrieas-formule hebt berekend, is het x-snijpunt van de symmetrieas.
3 Noteer de vergelijking van de symmetrieas. De waarde die u met uw symmetrieas-formule hebt berekend, is het x-snijpunt van de symmetrieas. - In het bovenstaande voorbeeld is de symmetrie-as -3/4.
Methode twee van twee:
De as van symmetrie grafisch vinden
-
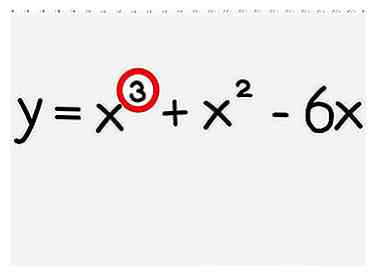 1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas vinden met behulp van de bovenstaande formulemethode. Gebruik de grafische methode als de graad van het polynoom hoger is dan 2.
1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas vinden met behulp van de bovenstaande formulemethode. Gebruik de grafische methode als de graad van het polynoom hoger is dan 2. -
 2 Teken de x- en y-assen. Maak twee lijnen in de vorm van een plusteken. De horizontale lijn is uw x-as; de verticale lijn is uw y-as.
2 Teken de x- en y-assen. Maak twee lijnen in de vorm van een plusteken. De horizontale lijn is uw x-as; de verticale lijn is uw y-as. -
 3 Nummer uw grafiek. Markeer beide assen met getallen op gelijke intervallen. De afstand moet uniform zijn op beide assen.
3 Nummer uw grafiek. Markeer beide assen met getallen op gelijke intervallen. De afstand moet uniform zijn op beide assen. -
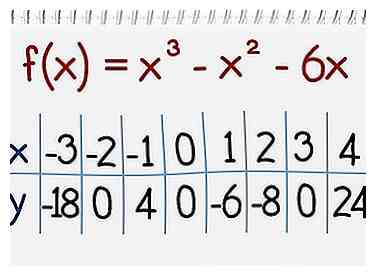 4 Bereken y = f (x) voor elke x. Neem uw polynoom of functie en bereken de waarden van f (x) door alle waarden van x erin te plaatsen.
4 Bereken y = f (x) voor elke x. Neem uw polynoom of functie en bereken de waarden van f (x) door alle waarden van x erin te plaatsen. -
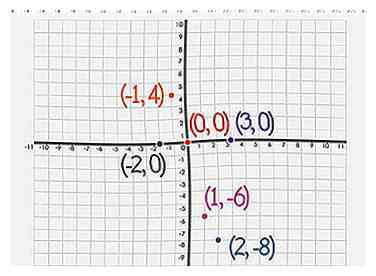 5 Maak een grafiekpunt voor elk paar. Je hebt nu paren van y = f (x) voor elke x op de as. Maak voor elk (x, y) -paar een punt op de grafiek - verticaal op de x-as en horizontaal op de y-as.
5 Maak een grafiekpunt voor elk paar. Je hebt nu paren van y = f (x) voor elke x op de as. Maak voor elk (x, y) -paar een punt op de grafiek - verticaal op de x-as en horizontaal op de y-as. -
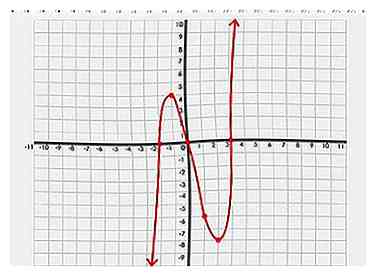 6 Teken de grafiek van de polynoom. Nadat u alle grafiekpunten hebt gemarkeerd, kunt u uw punten vloeiend verbinden om een ononderbroken grafiek van uw polynoom te onthullen.
6 Teken de grafiek van de polynoom. Nadat u alle grafiekpunten hebt gemarkeerd, kunt u uw punten vloeiend verbinden om een ononderbroken grafiek van uw polynoom te onthullen. -
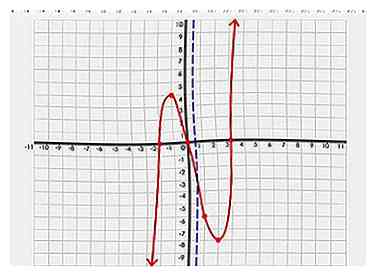 7 Zoek naar de symmetrieas. Inspecteer uw grafiek zorgvuldig. Zoek naar een punt op de as zodat wanneer er een lijn doorheen wordt gevoerd, de grafiek in twee gelijke gespiegelde helften splitst.
7 Zoek naar de symmetrieas. Inspecteer uw grafiek zorgvuldig. Zoek naar een punt op de as zodat wanneer er een lijn doorheen wordt gevoerd, de grafiek in twee gelijke gespiegelde helften splitst. -
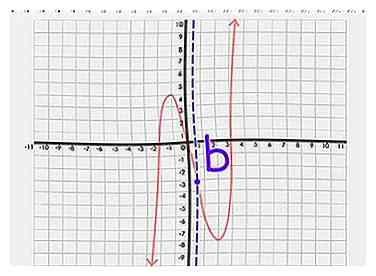 8 Let op de symmetrie-as. Als je een punt kunt vinden - noem het "b" - op de x-as die de grafiek in twee gespiegelde helften splitst, dan is dat punt, b, je symmetrie-as.
8 Let op de symmetrie-as. Als je een punt kunt vinden - noem het "b" - op de x-as die de grafiek in twee gespiegelde helften splitst, dan is dat punt, b, je symmetrie-as.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
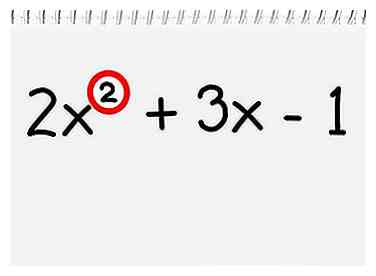 1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas met behulp van deze methode vinden. Gebruik methode 2 als de graad van het polynoom hoger is dan 2.
1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas met behulp van deze methode vinden. Gebruik methode 2 als de graad van het polynoom hoger is dan 2. 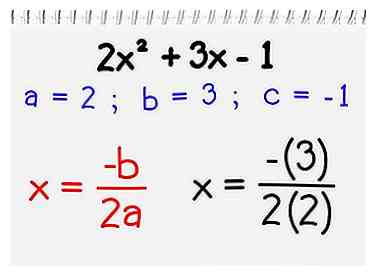 2 Steek uw nummers in de symmetrie-assen-formule. Om de symmetrieas te berekenen voor een 2e-orde polynoom in de formulierbijl2 + bx + c (een parabool), gebruik de basisformule x = -b / 2a.
2 Steek uw nummers in de symmetrie-assen-formule. Om de symmetrieas te berekenen voor een 2e-orde polynoom in de formulierbijl2 + bx + c (een parabool), gebruik de basisformule x = -b / 2a. 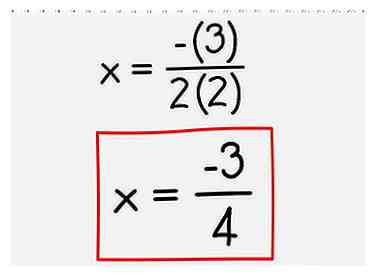 3 Noteer de vergelijking van de symmetrieas. De waarde die u met uw symmetrieas-formule hebt berekend, is het x-snijpunt van de symmetrieas.
3 Noteer de vergelijking van de symmetrieas. De waarde die u met uw symmetrieas-formule hebt berekend, is het x-snijpunt van de symmetrieas. 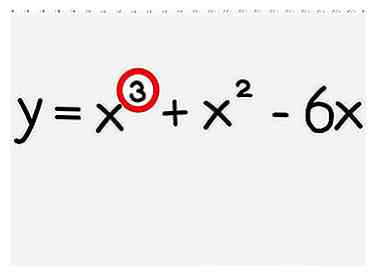 1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas vinden met behulp van de bovenstaande formulemethode. Gebruik de grafische methode als de graad van het polynoom hoger is dan 2.
1 Controleer de mate van uw polynoom. De graad (of "volgorde") van een polynoom is simpelweg de grootste exponentwaarde in de uitdrukking. Als de graad van uw polynoom 2 is (er is geen exponent groter dan x2), kunt u de symmetrieas vinden met behulp van de bovenstaande formulemethode. Gebruik de grafische methode als de graad van het polynoom hoger is dan 2.  2 Teken de x- en y-assen. Maak twee lijnen in de vorm van een plusteken. De horizontale lijn is uw x-as; de verticale lijn is uw y-as.
2 Teken de x- en y-assen. Maak twee lijnen in de vorm van een plusteken. De horizontale lijn is uw x-as; de verticale lijn is uw y-as.  3 Nummer uw grafiek. Markeer beide assen met getallen op gelijke intervallen. De afstand moet uniform zijn op beide assen.
3 Nummer uw grafiek. Markeer beide assen met getallen op gelijke intervallen. De afstand moet uniform zijn op beide assen. 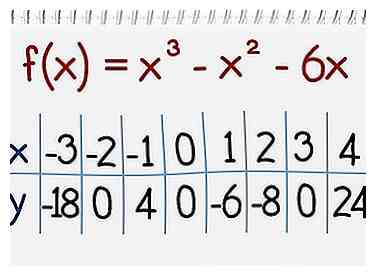 4 Bereken y = f (x) voor elke x. Neem uw polynoom of functie en bereken de waarden van f (x) door alle waarden van x erin te plaatsen.
4 Bereken y = f (x) voor elke x. Neem uw polynoom of functie en bereken de waarden van f (x) door alle waarden van x erin te plaatsen.  5 Maak een grafiekpunt voor elk paar. Je hebt nu paren van y = f (x) voor elke x op de as. Maak voor elk (x, y) -paar een punt op de grafiek - verticaal op de x-as en horizontaal op de y-as.
5 Maak een grafiekpunt voor elk paar. Je hebt nu paren van y = f (x) voor elke x op de as. Maak voor elk (x, y) -paar een punt op de grafiek - verticaal op de x-as en horizontaal op de y-as.  6 Teken de grafiek van de polynoom. Nadat u alle grafiekpunten hebt gemarkeerd, kunt u uw punten vloeiend verbinden om een ononderbroken grafiek van uw polynoom te onthullen.
6 Teken de grafiek van de polynoom. Nadat u alle grafiekpunten hebt gemarkeerd, kunt u uw punten vloeiend verbinden om een ononderbroken grafiek van uw polynoom te onthullen.  7 Zoek naar de symmetrieas. Inspecteer uw grafiek zorgvuldig. Zoek naar een punt op de as zodat wanneer er een lijn doorheen wordt gevoerd, de grafiek in twee gelijke gespiegelde helften splitst.
7 Zoek naar de symmetrieas. Inspecteer uw grafiek zorgvuldig. Zoek naar een punt op de as zodat wanneer er een lijn doorheen wordt gevoerd, de grafiek in twee gelijke gespiegelde helften splitst.  8 Let op de symmetrie-as. Als je een punt kunt vinden - noem het "b" - op de x-as die de grafiek in twee gespiegelde helften splitst, dan is dat punt, b, je symmetrie-as.
8 Let op de symmetrie-as. Als je een punt kunt vinden - noem het "b" - op de x-as die de grafiek in twee gespiegelde helften splitst, dan is dat punt, b, je symmetrie-as.