In algebra zijn binomials uitdrukkingen van twee termijnen die zijn verbonden aan een plusteken of minteken, zoals . De eerste term bevat altijd een variabele, terwijl de tweede term wel of niet mag. Het berekenen van een binomiaal betekent het vinden van eenvoudigere termen die, wanneer ze worden vermenigvuldigd, die binomiale uitdrukking produceren, die je helpt het op te lossen of te vereenvoudigen voor verder werk.
Deel een van de drie:
Factoring binomials
-
 1 Bekijk de basisprincipes van factoring. Factoring is wanneer u een groot aantal in zijn eenvoudigste deelbare delen opbreekt. Elk van deze onderdelen wordt een 'factor' genoemd. Het getal 6 kan dus bijvoorbeeld gelijk worden verdeeld door vier verschillende nummers: 1, 2, 3 en 6. Aldus zijn de factoren van 6 1, 2, 3 en 6.
1 Bekijk de basisprincipes van factoring. Factoring is wanneer u een groot aantal in zijn eenvoudigste deelbare delen opbreekt. Elk van deze onderdelen wordt een 'factor' genoemd. Het getal 6 kan dus bijvoorbeeld gelijk worden verdeeld door vier verschillende nummers: 1, 2, 3 en 6. Aldus zijn de factoren van 6 1, 2, 3 en 6. - De factoren van 32 zijn 1, 2, 4, 8, 16 en 32
- Zowel '1' als het aantal dat u factoring, zijn altijd factoren. Dus, de factoren van een klein aantal, zoals 3, zouden eenvoudigweg 1 en 3 zijn.
- Factoren zijn alleen de perfect deelbare getallen, of 'hele' getallen. Je kunt 32 delen door 3.564, of 21.4952, maar dit zal niet leiden tot een factor, alleen een andere decimaal.
-
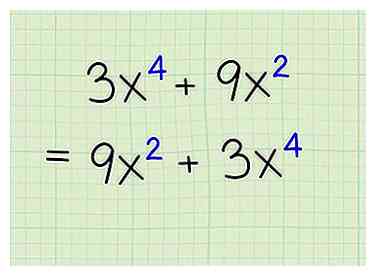 2 Plaats de voorwaarden van de binomiaal zodat ze gemakkelijker te lezen zijn. Een binomiaal is simpelweg het optellen of aftrekken van twee getallen, waarvan er tenminste één een variabele bevat. Soms hebben deze variabelen exponenten, zoals of . Bij het eerst factoring van binomials, kan het helpen om vergelijkingen opnieuw te ordenen met oplopende variabele termen, wat betekent dat de grootste exponent de laatste is. Bijvoorbeeld:
2 Plaats de voorwaarden van de binomiaal zodat ze gemakkelijker te lezen zijn. Een binomiaal is simpelweg het optellen of aftrekken van twee getallen, waarvan er tenminste één een variabele bevat. Soms hebben deze variabelen exponenten, zoals of . Bij het eerst factoring van binomials, kan het helpen om vergelijkingen opnieuw te ordenen met oplopende variabele termen, wat betekent dat de grootste exponent de laatste is. Bijvoorbeeld: - →
- →
- →
- Merk op hoe het negatieve teken voor de 2 blijft staan. Als een term wordt afgetrokken, houd dan gewoon het negatieve ervoor.
-
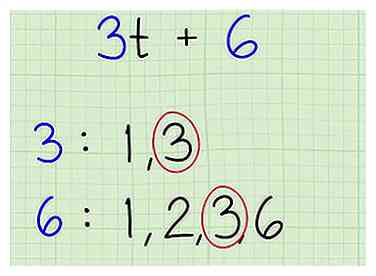 3 Zoek de grootste gemene deler van beide termen. Dit betekent dat je het hoogst mogelijke aantal vindt waarmee beide delen van de binomiaal deelbaar zijn. Als je het moeilijk hebt, kun je eenvoudig beide getallen op zichzelf filteren en vervolgens kijken wat het hoogste overeenkomende aantal is. Bijvoorbeeld:
3 Zoek de grootste gemene deler van beide termen. Dit betekent dat je het hoogst mogelijke aantal vindt waarmee beide delen van de binomiaal deelbaar zijn. Als je het moeilijk hebt, kun je eenvoudig beide getallen op zichzelf filteren en vervolgens kijken wat het hoogste overeenkomende aantal is. Bijvoorbeeld: - Praktijkprobleem:.
- Factoren van 3: 1, 3
- Factoren van 6: 1, 2, 3, 6.
- De grootste gemene deler is 3.
- Praktijkprobleem:.
-
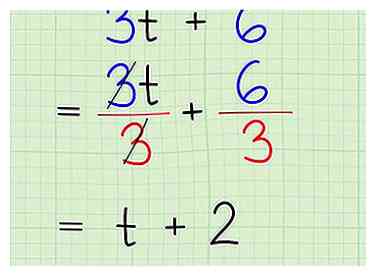 4 Verdeel de grootste gemene deler van elke term. Als u eenmaal weet wat uw gemeenschappelijke factor is, moet u deze van elke term verwijderen. Houd er echter rekening mee dat u eenvoudig de voorwaarden schendt en elke term verandert in een probleem met kleine divisies. Als je het goed hebt gedaan, zullen beide vergelijkingen je factor delen:
4 Verdeel de grootste gemene deler van elke term. Als u eenmaal weet wat uw gemeenschappelijke factor is, moet u deze van elke term verwijderen. Houd er echter rekening mee dat u eenvoudig de voorwaarden schendt en elke term verandert in een probleem met kleine divisies. Als je het goed hebt gedaan, zullen beide vergelijkingen je factor delen: - Praktijkprobleem:.
- Vind de grootste gemene deler: 3
- Verwijder factor uit beide termen:
-
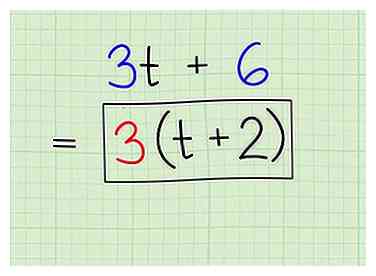 5 Vermenigvuldig je factor door de resulterende expressie om te voltooien. In het laatste probleem heb je een 3 verwijderd om te krijgen . Maar je verliet de drie niet alleen volledig, maar het eenvoudigweg uit te splitsen om dingen te vereenvoudigen. Je kunt niet zomaar nummers wissen zonder ze terug te zetten! Vermenigvuldig je factor met de uitdrukking om uiteindelijk te eindigen. Bijvoorbeeld:
5 Vermenigvuldig je factor door de resulterende expressie om te voltooien. In het laatste probleem heb je een 3 verwijderd om te krijgen . Maar je verliet de drie niet alleen volledig, maar het eenvoudigweg uit te splitsen om dingen te vereenvoudigen. Je kunt niet zomaar nummers wissen zonder ze terug te zetten! Vermenigvuldig je factor met de uitdrukking om uiteindelijk te eindigen. Bijvoorbeeld: - Praktijkprobleem:
- Vind de grootste gemene deler: 3
- Verwijder factor uit beide termen:
- Meervoudige factor door nieuwe uitdrukking:
- Eindelijk gefactored antwoord:
-
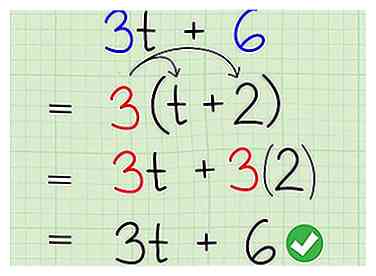 6 Controleer uw werk door alles te vermenigvuldigen met de oorspronkelijke vergelijking. Als je alles goed hebt gedaan, zou het eenvoudig moeten zijn om te controleren of je het goed hebt gedaan. Vermenigvuldig eenvoudig uw factor door beide afzonderlijke delen tussen haakjes. Als het overeenkomt met de originele, onwerkzaam gemaakte binomiale dan deed je het allemaal goed. Van begin tot eind, los de uitdrukking op om te oefenen:
6 Controleer uw werk door alles te vermenigvuldigen met de oorspronkelijke vergelijking. Als je alles goed hebt gedaan, zou het eenvoudig moeten zijn om te controleren of je het goed hebt gedaan. Vermenigvuldig eenvoudig uw factor door beide afzonderlijke delen tussen haakjes. Als het overeenkomt met de originele, onwerkzaam gemaakte binomiale dan deed je het allemaal goed. Van begin tot eind, los de uitdrukking op om te oefenen: - Reorganiseer termen:
- Vind de grootste gemene deler:
- Verwijder factor uit beide termen:
- Meervoudige factor door nieuwe uitdrukking:
- Antwoord nakijken:
Tweede deel van de drie:
Factoring binomials om vergelijkingen op te lossen
-
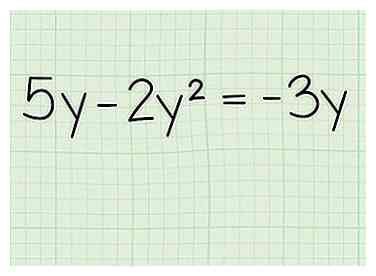 1 Gebruik factoring om vergelijkingen te vereenvoudigen en ze gemakkelijker op te lossen. Bij het oplossen van een vergelijking met binomials, met name complexe binomials, kan het lijken alsof er op geen enkele manier alles zal overeenkomen. Probeer bijvoorbeeld op te lossen . Eén manier om het op te lossen, vooral met exponenten, is om eerst factor te zijn.
1 Gebruik factoring om vergelijkingen te vereenvoudigen en ze gemakkelijker op te lossen. Bij het oplossen van een vergelijking met binomials, met name complexe binomials, kan het lijken alsof er op geen enkele manier alles zal overeenkomen. Probeer bijvoorbeeld op te lossen . Eén manier om het op te lossen, vooral met exponenten, is om eerst factor te zijn. - Praktijkprobleem:
- Onthoud dat binomials maar twee termen mogen hebben. Als er meer dan twee termen zijn, kun je in plaats daarvan polynomen leren oplossen.
-
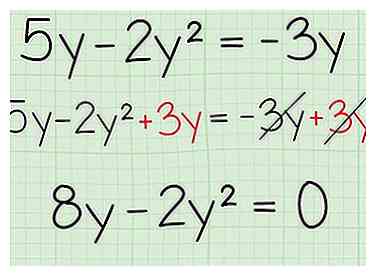 2 Optellen en aftrekken zodat de ene kant van de vergelijking gelijk is aan nul. Deze hele strategie is gebaseerd op een van de meest elementaire feiten van wiskunde: alles vermenigvuldigd met nul moet gelijk zijn aan nul. Dus als je vergelijking gelijk is aan nul, dan moet een van je gefactureerde termen gelijk zijn aan nul! Om te beginnen, optellen en aftrekken zodat één zijde gelijk is aan nul.
2 Optellen en aftrekken zodat de ene kant van de vergelijking gelijk is aan nul. Deze hele strategie is gebaseerd op een van de meest elementaire feiten van wiskunde: alles vermenigvuldigd met nul moet gelijk zijn aan nul. Dus als je vergelijking gelijk is aan nul, dan moet een van je gefactureerde termen gelijk zijn aan nul! Om te beginnen, optellen en aftrekken zodat één zijde gelijk is aan nul. - Praktijkprobleem:
- Zet op nul:
-
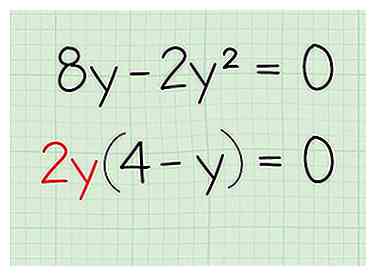 3 Factor de niet-nulzijde, net zoals normaal. Op dit punt kun je doen alsof de andere kant niet bestaat voor een stap. Zoek gewoon de grootste gemene deler, verdeelde deze uit en creëerde vervolgens uw uitgestelde uitdrukking.
3 Factor de niet-nulzijde, net zoals normaal. Op dit punt kun je doen alsof de andere kant niet bestaat voor een stap. Zoek gewoon de grootste gemene deler, verdeelde deze uit en creëerde vervolgens uw uitgestelde uitdrukking. - Praktijkprobleem:
- Zet op nul:
- Factor:
-
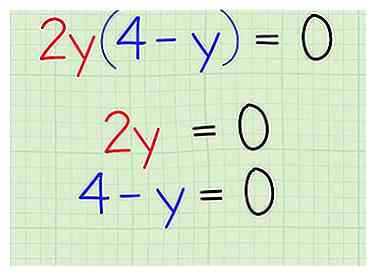 4 Stel zowel binnen als buiten de haakjes in als gelijk aan nul. In het oefenprobleem vermenigvuldig je 2j door 4 - y, en het moet gelijk zijn aan nul. Omdat alles vermenigvuldigd met nul gelijk is aan nul, betekent dit dat ofwel 2 of 4 - y 0 moet zijn. Creëer twee afzonderlijke vergelijkingen om erachter te komen wat y voor beide zijden gelijk moet zijn aan nul.
4 Stel zowel binnen als buiten de haakjes in als gelijk aan nul. In het oefenprobleem vermenigvuldig je 2j door 4 - y, en het moet gelijk zijn aan nul. Omdat alles vermenigvuldigd met nul gelijk is aan nul, betekent dit dat ofwel 2 of 4 - y 0 moet zijn. Creëer twee afzonderlijke vergelijkingen om erachter te komen wat y voor beide zijden gelijk moet zijn aan nul. - Praktijkprobleem:
- Zet op nul:
- Factor:
- Stel beide delen in op 0:
-
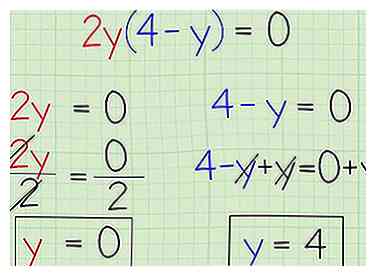 5 Los beide vergelijkingen op voor nul om uw definitieve antwoord of antwoorden te krijgen. Je hebt misschien één antwoord, of meer dan één antwoord. Onthoud dat slechts één zijde gelijk aan nul moet zijn, dus je zou een paar verschillende waarden van y kunnen krijgen die dezelfde vergelijking oplossen. Voor het einde van het oefenprobleem:
5 Los beide vergelijkingen op voor nul om uw definitieve antwoord of antwoorden te krijgen. Je hebt misschien één antwoord, of meer dan één antwoord. Onthoud dat slechts één zijde gelijk aan nul moet zijn, dus je zou een paar verschillende waarden van y kunnen krijgen die dezelfde vergelijking oplossen. Voor het einde van het oefenprobleem: -
- y = 0
-
- y = 4
-
-
 6 Sluit uw antwoorden weer aan om zeker te weten dat ze werken. Als je de juiste waarden voor y hebt, zou je ze moeten kunnen gebruiken om de vergelijking op te lossen. Het is eenvoudig om elke waarde van y uit te proberen in plaats van de variabele, zoals weergegeven. Omdat het antwoord y = 0 en y = 4 was:
6 Sluit uw antwoorden weer aan om zeker te weten dat ze werken. Als je de juiste waarden voor y hebt, zou je ze moeten kunnen gebruiken om de vergelijking op te lossen. Het is eenvoudig om elke waarde van y uit te proberen in plaats van de variabele, zoals weergegeven. Omdat het antwoord y = 0 en y = 4 was: -
- Dit antwoord is correct
-
- Dit antwoord is ook correct.
-
Derde deel van de drie:
Trickier-problemen oplossen
-
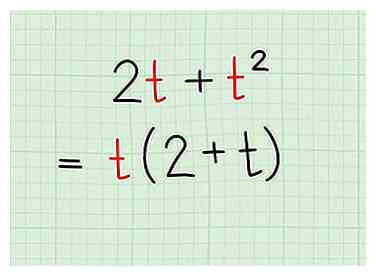 1 Vergeet niet dat variabelen ook als factoren gelden, zelfs met exponenten. Vergeet niet dat factoring uitzoekt welke getallen zich in het geheel kunnen verdelen. De uitdrukking is een andere manier om te zeggen . Dit betekent dat je elke x kunt weglaten als de andere term er ook een heeft. Behandel variabelen die niet verschillen van een normaal aantal. Bijvoorbeeld:
1 Vergeet niet dat variabelen ook als factoren gelden, zelfs met exponenten. Vergeet niet dat factoring uitzoekt welke getallen zich in het geheel kunnen verdelen. De uitdrukking is een andere manier om te zeggen . Dit betekent dat je elke x kunt weglaten als de andere term er ook een heeft. Behandel variabelen die niet verschillen van een normaal aantal. Bijvoorbeeld: - kan worden verwerkt, omdat beide termen een t bevatten. Je laatste antwoord zou zijn
- U kunt zelfs meerdere variabelen tegelijk verwijderen. Bijvoorbeeld in beide termen bevatten hetzelfde . Je kunt factor aan
-
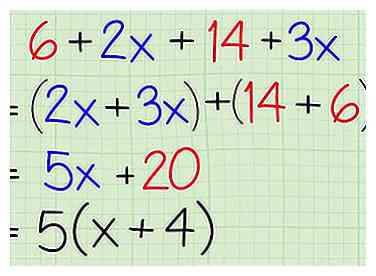 2 Herken niet-vereenvoudigde binomials door vergelijkbare termen te combineren. Neem bijvoorbeeld de uitdrukking . Dit lijkt misschien vier termen te hebben, maar kijk goed en je beseft dat er eigenlijk maar twee zijn. U kunt dezelfde termen toevoegen en aangezien zowel de 6 als de 14 geen variabele hebben en de 2x en 3x dezelfde variabele delen, kunnen deze beide worden gecombineerd. Factoring is dan eenvoudig:
2 Herken niet-vereenvoudigde binomials door vergelijkbare termen te combineren. Neem bijvoorbeeld de uitdrukking . Dit lijkt misschien vier termen te hebben, maar kijk goed en je beseft dat er eigenlijk maar twee zijn. U kunt dezelfde termen toevoegen en aangezien zowel de 6 als de 14 geen variabele hebben en de 2x en 3x dezelfde variabele delen, kunnen deze beide worden gecombineerd. Factoring is dan eenvoudig: - Origineel probleem:
- Reorganiseer termen:
- Combineer dezelfde voorwaarden:
- Vind de grootste gemene deler:
- Factor:
-
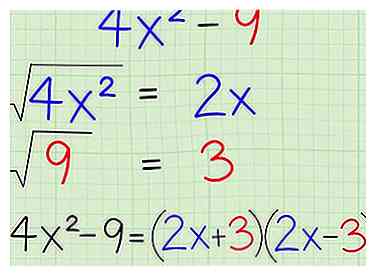 3 Herken het speciale "verschil van perfecte vierkanten."Een perfect vierkant is een getal waarvan de vierkantswortel een heel getal is, zoals , , of zelfs Als je binomiaal een aftrekprobleem is met twee perfecte vierkanten, zoals , u kunt ze simpelweg in deze formule pluggen:
3 Herken het speciale "verschil van perfecte vierkanten."Een perfect vierkant is een getal waarvan de vierkantswortel een heel getal is, zoals , , of zelfs Als je binomiaal een aftrekprobleem is met twee perfecte vierkanten, zoals , u kunt ze simpelweg in deze formule pluggen: - Het verschil in perfecte vierkantenformule:
- Praktijkprobleem:
- Vind wortels:
- Vierkanten in formule verbinden: [1]
-
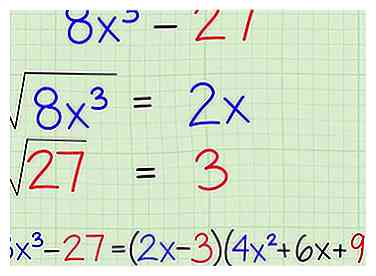 4 Leer het "verschil in perfecte kubussen" te doorbreken."Net als de perfecte vierkanten, is dit een eenvoudige formule voor wanneer je twee in blokjes uitgedrukte termen hebt afgetrokken door elkaar. . Net als eerder, vindt u eenvoudig de in blokjes gesneden wortel van elk, die u aansluit op een formule:
4 Leer het "verschil in perfecte kubussen" te doorbreken."Net als de perfecte vierkanten, is dit een eenvoudige formule voor wanneer je twee in blokjes uitgedrukte termen hebt afgetrokken door elkaar. . Net als eerder, vindt u eenvoudig de in blokjes gesneden wortel van elk, die u aansluit op een formule: - Verschil van perfecte kubussenformule:
- Praktijkprobleem:
- Zoek in blokjes gesneden wortels:
- Sluit kubussen aan in formule: [2]
-
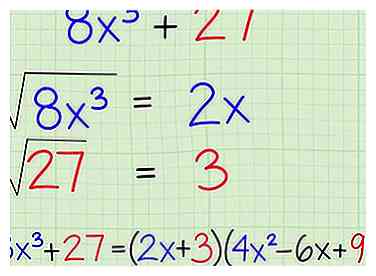 5 Weet dat de som van perfecte kubussen ook in een formule past. In tegenstelling tot het verschil in perfecte vierkanten, kun je eenvoudig ook toegevoegde kubussen vinden, zoals , met een eenvoudige formule. Het is bijna exact hetzelfde als hierboven, alleen met enkele plussen en minnen omgedraaid. De formule is net zo eenvoudig als de andere twee, en alles wat je hoeft te doen is de twee kubussen in het probleem herkennen om het te gebruiken:
5 Weet dat de som van perfecte kubussen ook in een formule past. In tegenstelling tot het verschil in perfecte vierkanten, kun je eenvoudig ook toegevoegde kubussen vinden, zoals , met een eenvoudige formule. Het is bijna exact hetzelfde als hierboven, alleen met enkele plussen en minnen omgedraaid. De formule is net zo eenvoudig als de andere twee, en alles wat je hoeft te doen is de twee kubussen in het probleem herkennen om het te gebruiken: - Som van de perfecte kubusformule:
- Praktijkprobleem:
- Zoek in blokjes gesneden wortels:
- Sluit kubussen aan in formule: [3]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bekijk de basisprincipes van factoring. Factoring is wanneer u een groot aantal in zijn eenvoudigste deelbare delen opbreekt. Elk van deze onderdelen wordt een 'factor' genoemd. Het getal 6 kan dus bijvoorbeeld gelijk worden verdeeld door vier verschillende nummers: 1, 2, 3 en 6. Aldus zijn de factoren van 6 1, 2, 3 en 6.
1 Bekijk de basisprincipes van factoring. Factoring is wanneer u een groot aantal in zijn eenvoudigste deelbare delen opbreekt. Elk van deze onderdelen wordt een 'factor' genoemd. Het getal 6 kan dus bijvoorbeeld gelijk worden verdeeld door vier verschillende nummers: 1, 2, 3 en 6. Aldus zijn de factoren van 6 1, 2, 3 en 6. 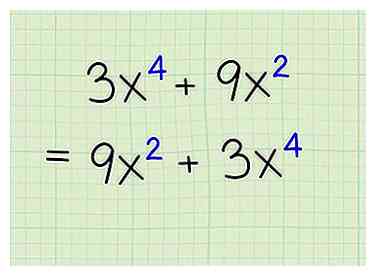 2 Plaats de voorwaarden van de binomiaal zodat ze gemakkelijker te lezen zijn. Een binomiaal is simpelweg het optellen of aftrekken van twee getallen, waarvan er tenminste één een variabele bevat. Soms hebben deze variabelen exponenten, zoals
2 Plaats de voorwaarden van de binomiaal zodat ze gemakkelijker te lezen zijn. Een binomiaal is simpelweg het optellen of aftrekken van twee getallen, waarvan er tenminste één een variabele bevat. Soms hebben deze variabelen exponenten, zoals 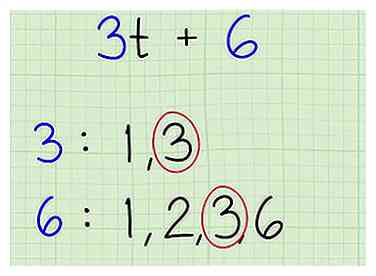 3 Zoek de grootste gemene deler van beide termen. Dit betekent dat je het hoogst mogelijke aantal vindt waarmee beide delen van de binomiaal deelbaar zijn. Als je het moeilijk hebt, kun je eenvoudig beide getallen op zichzelf filteren en vervolgens kijken wat het hoogste overeenkomende aantal is. Bijvoorbeeld:
3 Zoek de grootste gemene deler van beide termen. Dit betekent dat je het hoogst mogelijke aantal vindt waarmee beide delen van de binomiaal deelbaar zijn. Als je het moeilijk hebt, kun je eenvoudig beide getallen op zichzelf filteren en vervolgens kijken wat het hoogste overeenkomende aantal is. Bijvoorbeeld: 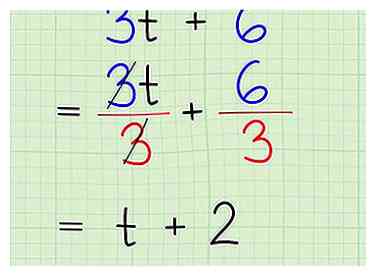 4 Verdeel de grootste gemene deler van elke term. Als u eenmaal weet wat uw gemeenschappelijke factor is, moet u deze van elke term verwijderen. Houd er echter rekening mee dat u eenvoudig de voorwaarden schendt en elke term verandert in een probleem met kleine divisies. Als je het goed hebt gedaan, zullen beide vergelijkingen je factor delen:
4 Verdeel de grootste gemene deler van elke term. Als u eenmaal weet wat uw gemeenschappelijke factor is, moet u deze van elke term verwijderen. Houd er echter rekening mee dat u eenvoudig de voorwaarden schendt en elke term verandert in een probleem met kleine divisies. Als je het goed hebt gedaan, zullen beide vergelijkingen je factor delen: 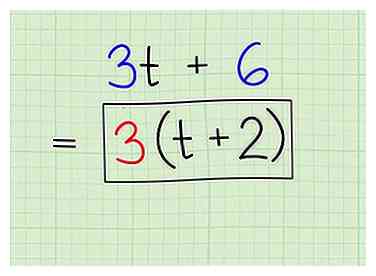 5 Vermenigvuldig je factor door de resulterende expressie om te voltooien. In het laatste probleem heb je een 3 verwijderd om te krijgen
5 Vermenigvuldig je factor door de resulterende expressie om te voltooien. In het laatste probleem heb je een 3 verwijderd om te krijgen 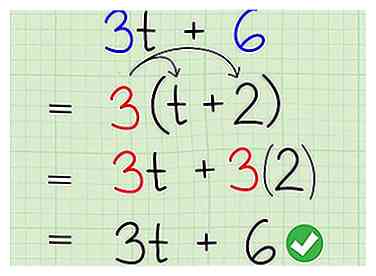 6 Controleer uw werk door alles te vermenigvuldigen met de oorspronkelijke vergelijking. Als je alles goed hebt gedaan, zou het eenvoudig moeten zijn om te controleren of je het goed hebt gedaan. Vermenigvuldig eenvoudig uw factor door beide afzonderlijke delen tussen haakjes. Als het overeenkomt met de originele, onwerkzaam gemaakte binomiale dan deed je het allemaal goed. Van begin tot eind, los de uitdrukking op
6 Controleer uw werk door alles te vermenigvuldigen met de oorspronkelijke vergelijking. Als je alles goed hebt gedaan, zou het eenvoudig moeten zijn om te controleren of je het goed hebt gedaan. Vermenigvuldig eenvoudig uw factor door beide afzonderlijke delen tussen haakjes. Als het overeenkomt met de originele, onwerkzaam gemaakte binomiale dan deed je het allemaal goed. Van begin tot eind, los de uitdrukking op 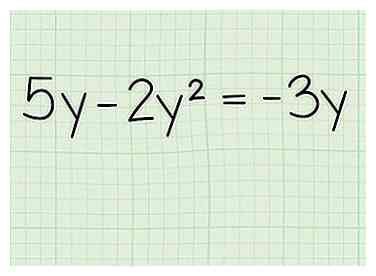 1 Gebruik factoring om vergelijkingen te vereenvoudigen en ze gemakkelijker op te lossen. Bij het oplossen van een vergelijking met binomials, met name complexe binomials, kan het lijken alsof er op geen enkele manier alles zal overeenkomen. Probeer bijvoorbeeld op te lossen
1 Gebruik factoring om vergelijkingen te vereenvoudigen en ze gemakkelijker op te lossen. Bij het oplossen van een vergelijking met binomials, met name complexe binomials, kan het lijken alsof er op geen enkele manier alles zal overeenkomen. Probeer bijvoorbeeld op te lossen 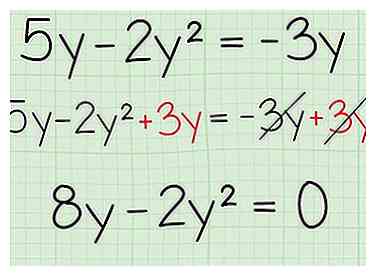 2 Optellen en aftrekken zodat de ene kant van de vergelijking gelijk is aan nul. Deze hele strategie is gebaseerd op een van de meest elementaire feiten van wiskunde: alles vermenigvuldigd met nul moet gelijk zijn aan nul. Dus als je vergelijking gelijk is aan nul, dan moet een van je gefactureerde termen gelijk zijn aan nul! Om te beginnen, optellen en aftrekken zodat één zijde gelijk is aan nul.
2 Optellen en aftrekken zodat de ene kant van de vergelijking gelijk is aan nul. Deze hele strategie is gebaseerd op een van de meest elementaire feiten van wiskunde: alles vermenigvuldigd met nul moet gelijk zijn aan nul. Dus als je vergelijking gelijk is aan nul, dan moet een van je gefactureerde termen gelijk zijn aan nul! Om te beginnen, optellen en aftrekken zodat één zijde gelijk is aan nul. 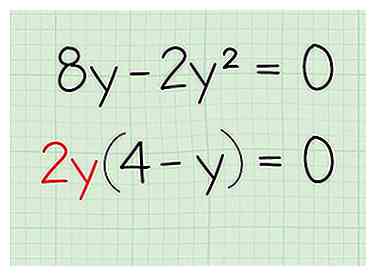 3 Factor de niet-nulzijde, net zoals normaal. Op dit punt kun je doen alsof de andere kant niet bestaat voor een stap. Zoek gewoon de grootste gemene deler, verdeelde deze uit en creëerde vervolgens uw uitgestelde uitdrukking.
3 Factor de niet-nulzijde, net zoals normaal. Op dit punt kun je doen alsof de andere kant niet bestaat voor een stap. Zoek gewoon de grootste gemene deler, verdeelde deze uit en creëerde vervolgens uw uitgestelde uitdrukking. 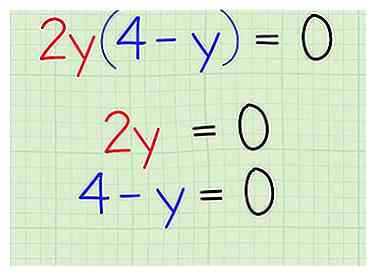 4 Stel zowel binnen als buiten de haakjes in als gelijk aan nul. In het oefenprobleem vermenigvuldig je 2j door 4 - y, en het moet gelijk zijn aan nul. Omdat alles vermenigvuldigd met nul gelijk is aan nul, betekent dit dat ofwel 2 of 4 - y 0 moet zijn. Creëer twee afzonderlijke vergelijkingen om erachter te komen wat y voor beide zijden gelijk moet zijn aan nul.
4 Stel zowel binnen als buiten de haakjes in als gelijk aan nul. In het oefenprobleem vermenigvuldig je 2j door 4 - y, en het moet gelijk zijn aan nul. Omdat alles vermenigvuldigd met nul gelijk is aan nul, betekent dit dat ofwel 2 of 4 - y 0 moet zijn. Creëer twee afzonderlijke vergelijkingen om erachter te komen wat y voor beide zijden gelijk moet zijn aan nul. 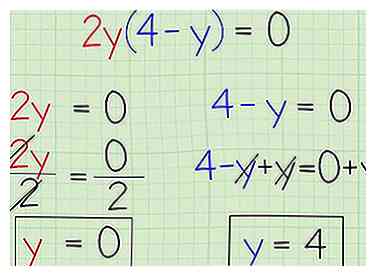 5 Los beide vergelijkingen op voor nul om uw definitieve antwoord of antwoorden te krijgen. Je hebt misschien één antwoord, of meer dan één antwoord. Onthoud dat slechts één zijde gelijk aan nul moet zijn, dus je zou een paar verschillende waarden van y kunnen krijgen die dezelfde vergelijking oplossen. Voor het einde van het oefenprobleem:
5 Los beide vergelijkingen op voor nul om uw definitieve antwoord of antwoorden te krijgen. Je hebt misschien één antwoord, of meer dan één antwoord. Onthoud dat slechts één zijde gelijk aan nul moet zijn, dus je zou een paar verschillende waarden van y kunnen krijgen die dezelfde vergelijking oplossen. Voor het einde van het oefenprobleem:  6 Sluit uw antwoorden weer aan om zeker te weten dat ze werken. Als je de juiste waarden voor y hebt, zou je ze moeten kunnen gebruiken om de vergelijking op te lossen. Het is eenvoudig om elke waarde van y uit te proberen in plaats van de variabele, zoals weergegeven. Omdat het antwoord y = 0 en y = 4 was:
6 Sluit uw antwoorden weer aan om zeker te weten dat ze werken. Als je de juiste waarden voor y hebt, zou je ze moeten kunnen gebruiken om de vergelijking op te lossen. Het is eenvoudig om elke waarde van y uit te proberen in plaats van de variabele, zoals weergegeven. Omdat het antwoord y = 0 en y = 4 was: 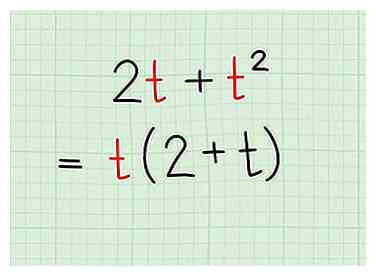 1 Vergeet niet dat variabelen ook als factoren gelden, zelfs met exponenten. Vergeet niet dat factoring uitzoekt welke getallen zich in het geheel kunnen verdelen. De uitdrukking
1 Vergeet niet dat variabelen ook als factoren gelden, zelfs met exponenten. Vergeet niet dat factoring uitzoekt welke getallen zich in het geheel kunnen verdelen. De uitdrukking 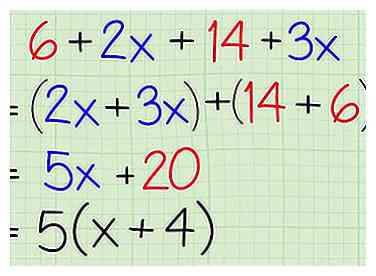 2 Herken niet-vereenvoudigde binomials door vergelijkbare termen te combineren. Neem bijvoorbeeld de uitdrukking
2 Herken niet-vereenvoudigde binomials door vergelijkbare termen te combineren. Neem bijvoorbeeld de uitdrukking 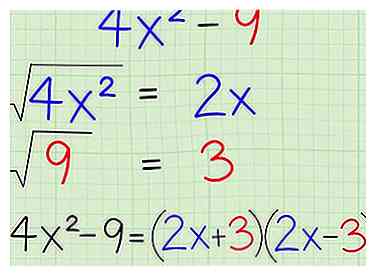 3 Herken het speciale "verschil van perfecte vierkanten."Een perfect vierkant is een getal waarvan de vierkantswortel een heel getal is, zoals
3 Herken het speciale "verschil van perfecte vierkanten."Een perfect vierkant is een getal waarvan de vierkantswortel een heel getal is, zoals 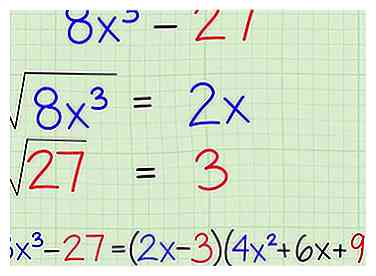 4 Leer het "verschil in perfecte kubussen" te doorbreken."Net als de perfecte vierkanten, is dit een eenvoudige formule voor wanneer je twee in blokjes uitgedrukte termen hebt afgetrokken door elkaar.
4 Leer het "verschil in perfecte kubussen" te doorbreken."Net als de perfecte vierkanten, is dit een eenvoudige formule voor wanneer je twee in blokjes uitgedrukte termen hebt afgetrokken door elkaar. 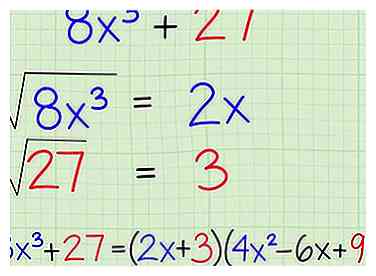 5 Weet dat de som van perfecte kubussen ook in een formule past. In tegenstelling tot het verschil in perfecte vierkanten, kun je eenvoudig ook toegevoegde kubussen vinden, zoals
5 Weet dat de som van perfecte kubussen ook in een formule past. In tegenstelling tot het verschil in perfecte vierkanten, kun je eenvoudig ook toegevoegde kubussen vinden, zoals