Dit is een artikel over hoe een 3 te ontbindenrd graden polynoom. We zullen onderzoeken hoe we het gebruik van groepering kunnen factoreren en hoe we de factoren van de vrije term kunnen gebruiken.
Deel een van de twee:
Factoring door groeperen
-
 1 Groepeer het polynoom in twee delen. Door de polynoom in twee secties te groeperen, kun je elke sectie afzonderlijk aanvallen.
1 Groepeer het polynoom in twee delen. Door de polynoom in twee secties te groeperen, kun je elke sectie afzonderlijk aanvallen. - Stel dat we met de polynoom x werken3 + 3x2 - 6x - 18 = 0. Laten we het groeperen in (x3 + 3x2) en (- 6x - 18)
-
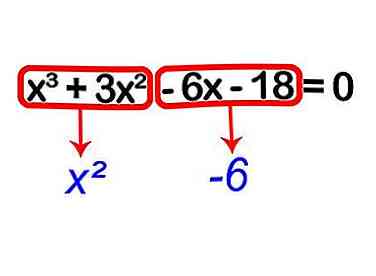 2 Zoek naar wat gebruikelijk is in elke sectie.
2 Zoek naar wat gebruikelijk is in elke sectie. - Kijkend naar (x3 + 3x2), we kunnen dat zien x2 komt veel voor.
- Kijkend naar (- 6x - 18), kunnen we zien dat -6 gebruikelijk is.
-
 3 Factor de overeenkomsten van de twee voorwaarden.
3 Factor de overeenkomsten van de twee voorwaarden. - Factoren uit x2 uit het eerste gedeelte krijgen we x2(x + 3).
- Als u uit het tweede gedeelte uit -6 wegvalt, krijgt u -6 (x + 3).
-
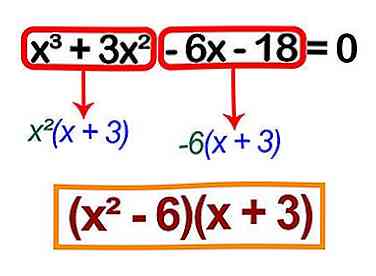 4 Als elk van de twee termen dezelfde factor bevat, kunt u de factoren samen combineren.
4 Als elk van de twee termen dezelfde factor bevat, kunt u de factoren samen combineren. - Dit geeft je (x + 3) (x2 - 6).
-
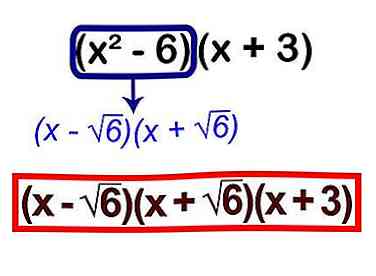 5 Zoek de oplossing door naar de wortels te kijken. Als je een x hebt2 in je roots, onthoud dat beide negatieve en positieve getallen voldoen aan die vergelijking.
5 Zoek de oplossing door naar de wortels te kijken. Als je een x hebt2 in je roots, onthoud dat beide negatieve en positieve getallen voldoen aan die vergelijking. - De oplossingen zijn -3, √6 en -√6.
Deel twee van twee:
Factoren met behulp van de vrije termijn
-
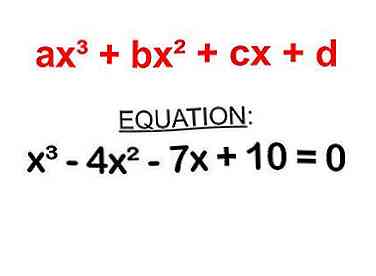 1 Herschik de uitdrukking zodat deze in de vorm van aX is3+ bX2+ CX + d.
1 Herschik de uitdrukking zodat deze in de vorm van aX is3+ bX2+ CX + d. - Laten we zeggen dat je met de vergelijking werkt: x3 - 4x2 - 7x + 10 = 0.
-
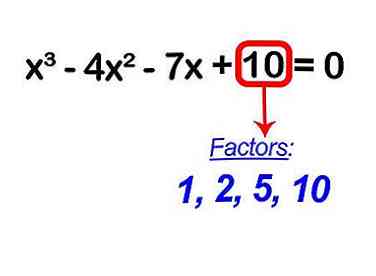 2 Zoek alle factoren van "d". De constante "d" zal het getal zijn dat geen variabelen bevat, zoals "x", ernaast.
2 Zoek alle factoren van "d". De constante "d" zal het getal zijn dat geen variabelen bevat, zoals "x", ernaast. - Factoren zijn de getallen die u kunt vermenigvuldigen om een ander nummer te krijgen. In uw geval zijn de factoren 10 of "d": 1, 2, 5 en 10.
-
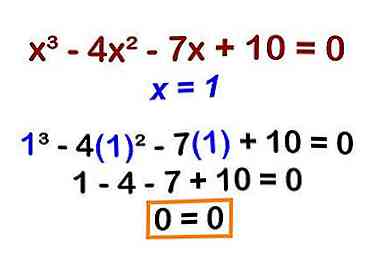 3 Zoek een factor die ervoor zorgt dat de polynoom gelijk is aan nul. We willen bepalen welke factor de polynoom gelijk aan nul maakt wanneer we de factor vervangen door elke "x" in de vergelijking.
3 Zoek een factor die ervoor zorgt dat de polynoom gelijk is aan nul. We willen bepalen welke factor de polynoom gelijk aan nul maakt wanneer we de factor vervangen door elke "x" in de vergelijking. - Begin met uw eerste factor, 1. Vervang "1" voor elke "x" in de vergelijking:
(1)3 - 4(1)2 - 7(1) + 10 = 0 - Dit geeft je: 1 - 4 - 7 + 10 = 0.
- Omdat 0 = 0 een echte verklaring is, weet u dat x = 1 een oplossing is.
- Begin met uw eerste factor, 1. Vervang "1" voor elke "x" in de vergelijking:
-
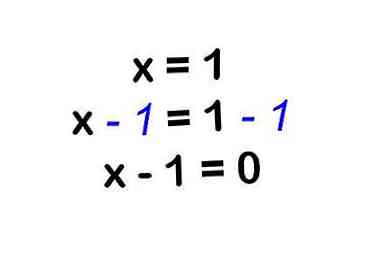 4 Doe een beetje herschikken. Als x = 1, kunt u de instructie anders rangschikken om er een beetje anders uit te zien zonder te veranderen wat het betekent.
4 Doe een beetje herschikken. Als x = 1, kunt u de instructie anders rangschikken om er een beetje anders uit te zien zonder te veranderen wat het betekent. - "x = 1" is hetzelfde als "x - 1 = 0" of "(x - 1)". Je hebt zojuist een "1" afgetrokken van elke kant van de vergelijking.
-
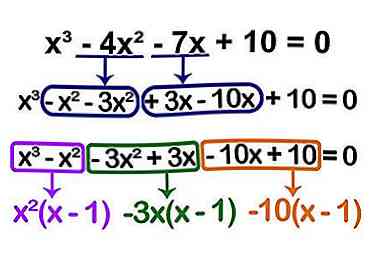 5 Bepaal uw wortel uit de rest van de vergelijking. "(x - 1)" is onze root. Kijk of je het uit de rest van de vergelijking kunt weglaten. Neem het een polynoom per keer.
5 Bepaal uw wortel uit de rest van de vergelijking. "(x - 1)" is onze root. Kijk of je het uit de rest van de vergelijking kunt weglaten. Neem het een polynoom per keer. - Kun je factor (x - 1) uit de x halen3? Nee dat kan niet. Maar je kunt een -x lenen2 van de tweede variabele; dan factor: x2(x - 1) = x3 - x2.
- Kun je factor (x - 1) uitsluiten van wat er overblijft van je tweede variabele? Nee, nogmaals, dat kan niet. Je moet nog een klein beetje lenen van de derde variabele. Je moet een 3x van -7x lenen. Dit geeft je -3x (x - 1) = -3x2 + 3x.
- Omdat je een 3x hebt genomen van -7x, is onze derde variabele nu -10x en onze constante is 10. Kun je dit factoreren? Jij kan! -10 (x - 1) = -10x + 10.
- Wat je deed was de variabelen herschikken, zodat je een (x - 1) uit de hele vergelijking kon weglaten. Je herschikte vergelijking ziet er als volgt uit: x3 - x2 - 3x2 + 3x - 10x + 10 = 0, maar het is nog steeds hetzelfde als x3 - 4x2 - 7x + 10 = 0.
-
 6 Blijf vervangen door de factoren van de vrije termijn. Kijk naar de cijfers die je hebt weggelaten met de (x - 1) in stap 5:
6 Blijf vervangen door de factoren van de vrije termijn. Kijk naar de cijfers die je hebt weggelaten met de (x - 1) in stap 5: - X2(x - 1) - 3x (x - 1) - 10 (x - 1) = 0. Je kunt dit herschikken om het nog een stuk eenvoudiger te maken om nog een factor te factoreren: (x - 1) (x2 - 3x - 10) = 0.
- Je probeert alleen te factor (x2 - 3x - 10) hier. Deze factor komt voor in (x + 2) (x - 5).
-
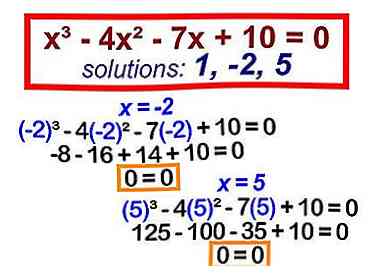 7 Uw oplossingen zullen de gefactureerde wortels zijn. U kunt controleren of uw oplossingen echt werken door ze allemaal afzonderlijk in de oorspronkelijke vergelijking in te voegen.
7 Uw oplossingen zullen de gefactureerde wortels zijn. U kunt controleren of uw oplossingen echt werken door ze allemaal afzonderlijk in de oorspronkelijke vergelijking in te voegen. - (x - 1) (x + 2) (x - 5) = 0 Dit geeft oplossingen van 1, -2 en 5.
- Sluit -2 terug in de vergelijking: (-2)3 - 4(-2)2 - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0.
- Sluit 5 weer aan op de vergelijking: (5)3 - 4(5)2 - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Groepeer het polynoom in twee delen. Door de polynoom in twee secties te groeperen, kun je elke sectie afzonderlijk aanvallen.
1 Groepeer het polynoom in twee delen. Door de polynoom in twee secties te groeperen, kun je elke sectie afzonderlijk aanvallen. 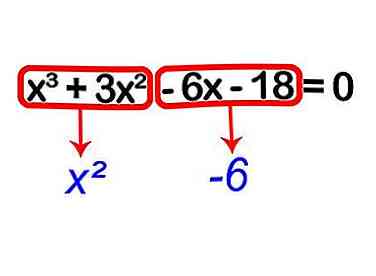 2 Zoek naar wat gebruikelijk is in elke sectie.
2 Zoek naar wat gebruikelijk is in elke sectie.  3 Factor de overeenkomsten van de twee voorwaarden.
3 Factor de overeenkomsten van de twee voorwaarden. 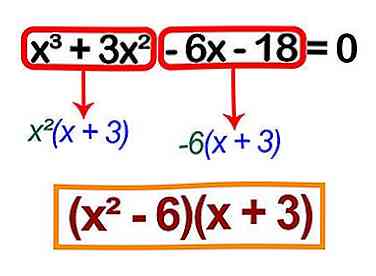 4 Als elk van de twee termen dezelfde factor bevat, kunt u de factoren samen combineren.
4 Als elk van de twee termen dezelfde factor bevat, kunt u de factoren samen combineren. 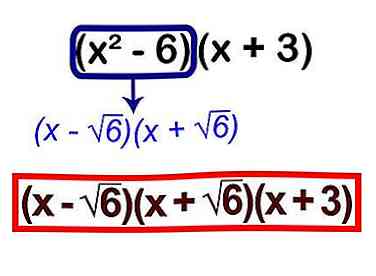 5 Zoek de oplossing door naar de wortels te kijken. Als je een x hebt2 in je roots, onthoud dat beide negatieve en positieve getallen voldoen aan die vergelijking.
5 Zoek de oplossing door naar de wortels te kijken. Als je een x hebt2 in je roots, onthoud dat beide negatieve en positieve getallen voldoen aan die vergelijking. 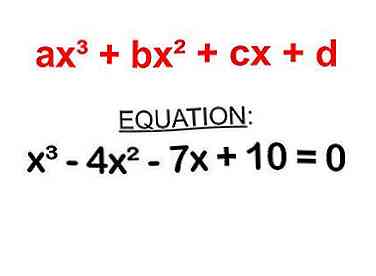 1 Herschik de uitdrukking zodat deze in de vorm van aX is3+ bX2+ CX + d.
1 Herschik de uitdrukking zodat deze in de vorm van aX is3+ bX2+ CX + d. 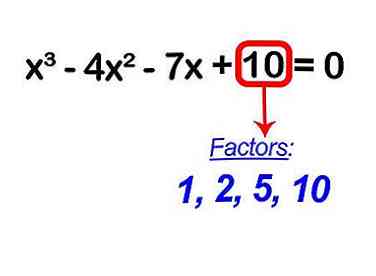 2 Zoek alle factoren van "d". De constante "d" zal het getal zijn dat geen variabelen bevat, zoals "x", ernaast.
2 Zoek alle factoren van "d". De constante "d" zal het getal zijn dat geen variabelen bevat, zoals "x", ernaast. 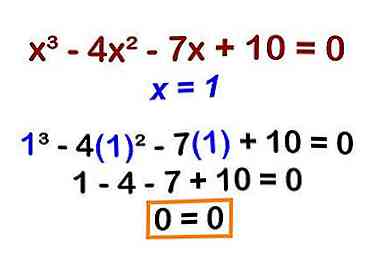 3 Zoek een factor die ervoor zorgt dat de polynoom gelijk is aan nul. We willen bepalen welke factor de polynoom gelijk aan nul maakt wanneer we de factor vervangen door elke "x" in de vergelijking.
3 Zoek een factor die ervoor zorgt dat de polynoom gelijk is aan nul. We willen bepalen welke factor de polynoom gelijk aan nul maakt wanneer we de factor vervangen door elke "x" in de vergelijking. 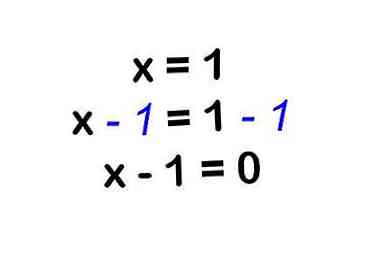 4 Doe een beetje herschikken. Als x = 1, kunt u de instructie anders rangschikken om er een beetje anders uit te zien zonder te veranderen wat het betekent.
4 Doe een beetje herschikken. Als x = 1, kunt u de instructie anders rangschikken om er een beetje anders uit te zien zonder te veranderen wat het betekent. 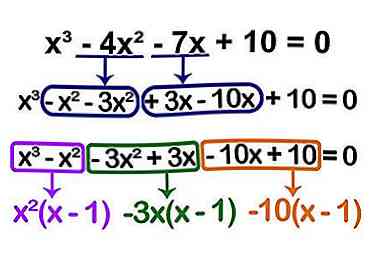 5 Bepaal uw wortel uit de rest van de vergelijking. "(x - 1)" is onze root. Kijk of je het uit de rest van de vergelijking kunt weglaten. Neem het een polynoom per keer.
5 Bepaal uw wortel uit de rest van de vergelijking. "(x - 1)" is onze root. Kijk of je het uit de rest van de vergelijking kunt weglaten. Neem het een polynoom per keer.  6 Blijf vervangen door de factoren van de vrije termijn. Kijk naar de cijfers die je hebt weggelaten met de (x - 1) in stap 5:
6 Blijf vervangen door de factoren van de vrije termijn. Kijk naar de cijfers die je hebt weggelaten met de (x - 1) in stap 5: 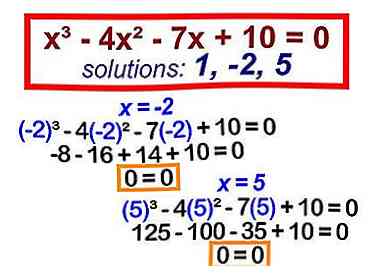 7 Uw oplossingen zullen de gefactureerde wortels zijn. U kunt controleren of uw oplossingen echt werken door ze allemaal afzonderlijk in de oorspronkelijke vergelijking in te voegen.
7 Uw oplossingen zullen de gefactureerde wortels zijn. U kunt controleren of uw oplossingen echt werken door ze allemaal afzonderlijk in de oorspronkelijke vergelijking in te voegen.