Als u weet hoe u twee matrices tegelijk kunt vermenigvuldigen, bent u goed op weg om de ene matrix door de andere te 'delen'. Dat woord staat tussen aanhalingstekens omdat matrices technisch gezien niet kunnen worden opgedeeld. In plaats daarvan vermenigvuldigen we één matrix met de omgekeerde van een andere matrix. Deze berekeningen worden vaak gebruikt om systemen van lineaire vergelijkingen op te lossen.[1]
Deel een van de drie:
Bevestigen dat "verdeling" mogelijk is
-
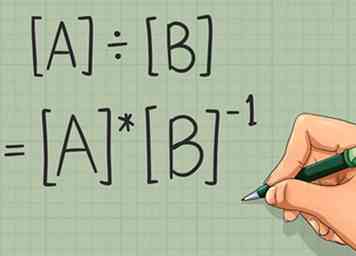 1 Begrijp matrix "verdeling." Technisch gezien bestaat er niet zoiets als matrixverdeling. Het verdelen van een matrix door een andere matrix is een ongedefinieerde functie.[2] Het dichtstbijzijnde equivalent vermenigvuldigt zich met de inverse van een andere matrix. Met andere woorden, terwijl [A] ÷ [B] niet is gedefinieerd, kunt u het probleem oplossen [A] * [B]-1. Aangezien deze twee vergelijkingen hetzelfde zouden zijn voor scalaire grootheden, voelt dit als matrixverdeling, maar het is belangrijk om de juiste terminologie te gebruiken.
1 Begrijp matrix "verdeling." Technisch gezien bestaat er niet zoiets als matrixverdeling. Het verdelen van een matrix door een andere matrix is een ongedefinieerde functie.[2] Het dichtstbijzijnde equivalent vermenigvuldigt zich met de inverse van een andere matrix. Met andere woorden, terwijl [A] ÷ [B] niet is gedefinieerd, kunt u het probleem oplossen [A] * [B]-1. Aangezien deze twee vergelijkingen hetzelfde zouden zijn voor scalaire grootheden, voelt dit als matrixverdeling, maar het is belangrijk om de juiste terminologie te gebruiken. - Merk op dat [A] * [B]-1 en B]-1 * [A] zijn niet hetzelfde probleem. Mogelijk moet u beide oplossen om alle mogelijke oplossingen te vinden.
- Bijvoorbeeld in plaats van , schrijven .
U moet mogelijk ook berekenen , wat een ander antwoord kan hebben.
-
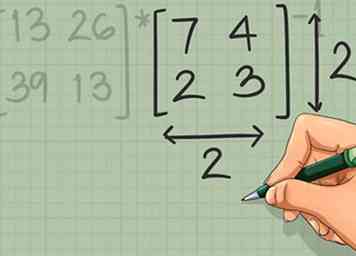 2 Bevestig dat de "delermatrix" vierkant is. Om de inverse van een matrix te nemen, moet deze een vierkante matrix zijn met hetzelfde aantal rijen en kolommen. Als de matrix die u van plan bent te omkeren niet-vierkant is, is er geen unieke oplossing voor het probleem.[3]
2 Bevestig dat de "delermatrix" vierkant is. Om de inverse van een matrix te nemen, moet deze een vierkante matrix zijn met hetzelfde aantal rijen en kolommen. Als de matrix die u van plan bent te omkeren niet-vierkant is, is er geen unieke oplossing voor het probleem.[3] - De term "matrix van de deler" is een beetje los, omdat dit technisch gezien geen verdeeldheidsprobleem is. Voor [A] * [B]-1, dit verwijst naar matrix [B]. In ons voorbeeldprobleem is dit .
- Een matrix met een inverse wordt "inverteerbaar" of "niet-enkelvoudig" genoemd. Matrices zonder een inverse zijn "enkelvoud".
-
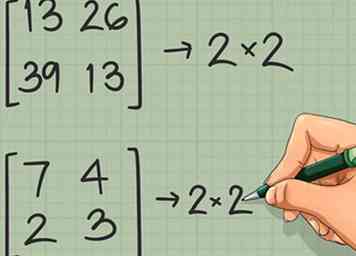 3 Controleer of de twee matrices samen kunnen worden vermenigvuldigd. Om twee matrices samen te vermenigvuldigen, moet het aantal kolommen in de eerste matrix gelijk zijn aan het aantal rijen in de tweede matrix.[4] Als dit niet werkt in beide regelingen ([A] * [B]-1 of [B]-1 * [A]), er is geen oplossing voor het probleem.
3 Controleer of de twee matrices samen kunnen worden vermenigvuldigd. Om twee matrices samen te vermenigvuldigen, moet het aantal kolommen in de eerste matrix gelijk zijn aan het aantal rijen in de tweede matrix.[4] Als dit niet werkt in beide regelingen ([A] * [B]-1 of [B]-1 * [A]), er is geen oplossing voor het probleem. - Als [A] bijvoorbeeld een matrix van 4 x 3 is (4 rijen, 3 kolommen) en [B] een matrix van 2 x 2 (2 rijen, 2 kolommen), is er geen oplossing. [A] * [B]-1 werkt niet sinds 3 ≠ 2 en [B]-1 * [A] werkt niet sinds 2 ≠ 4.
- Merk op dat de inverse [B]-1 heeft altijd hetzelfde aantal rijen en kolommen als de oorspronkelijke matrix [B]. Het is niet nodig om de inverse te berekenen om deze stap te voltooien.
- In ons voorbeeldprobleem zijn beide matrices 2 x 2s, dus ze kunnen in elke volgorde worden vermenigvuldigd.
-
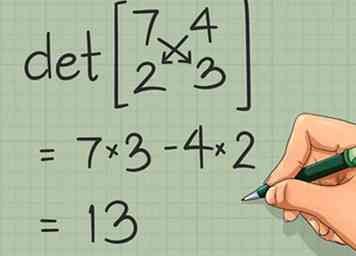 4 Zoek de determinant van een matrix van 2 x 2. Er is nog een vereiste om te controleren voordat u de inverse van een matrix kunt nemen. De determinant van de matrix moet niet-nul zijn. Als de determinant nul is, heeft de matrix geen inverse. U kunt de determinant in het eenvoudigste geval als de 2 x 2 matrix vinden:
4 Zoek de determinant van een matrix van 2 x 2. Er is nog een vereiste om te controleren voordat u de inverse van een matrix kunt nemen. De determinant van de matrix moet niet-nul zijn. Als de determinant nul is, heeft de matrix geen inverse. U kunt de determinant in het eenvoudigste geval als de 2 x 2 matrix vinden: - 2 x 2 matrix: De determinant van de matrix is ad - bc.[5] Met andere woorden, neem het product van de hoofddiagonaal (van linksboven naar rechtsonder) en trek vervolgens het product van de antidiagonaal (rechtsboven naar linksonder) af.
- Bijvoorbeeld de matrix heeft de determinant (7) (3) - (4) (2) = 21 - 8 = 13. Dit is niet-nul, dus het is mogelijk om de inverse te vinden.
-
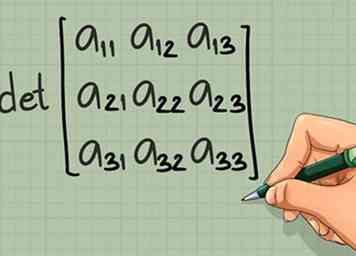 5 Zoek de determinant van een grotere matrix. Als uw matrix 3 x 3 of groter is, kost het vinden van de determinant wat meer werk:
5 Zoek de determinant van een grotere matrix. Als uw matrix 3 x 3 of groter is, kost het vinden van de determinant wat meer werk: - 3 x 3 matrix: Kies een willekeurig element en haal de rij en kolom uit waartoe het behoort. Zoek de determinant van de resterende 2 x 2 matrix, vermenigvuldig dit met het gekozen element en verwijs naar een matrixtekenkaart om het teken te bepalen. Herhaal dit voor de andere twee elementen in dezelfde rij of kolom als de eerste die u hebt gekozen en tel dan alle drie de determinanten op. Lees dit artikel voor stapsgewijze instructies en tips om dit te versnellen.
- Grotere matrices: Het gebruik van een grafische rekenmachine of software wordt aanbevolen. De methode is vergelijkbaar met de 3 x 3 matrixmethode, maar is met de hand vervelend.[6] Om bijvoorbeeld de determinant van een matrix van 4 x 4 te vinden, moet u de determinanten van vier 3 x 3-matrices vinden.
-
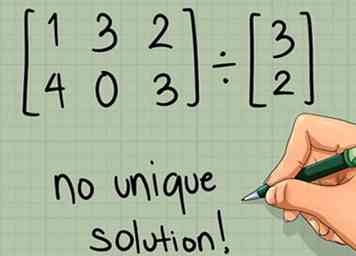 6 Ga door. Als uw matrix niet vierkant is of als de determinant nul is, schrijft u 'geen unieke oplossing'. Het probleem is voltooid. Als de matrix vierkant is en de bepalende factor niet nul is, gaat u door naar het volgende gedeelte voor de volgende stap: het vinden van het omgekeerde.
6 Ga door. Als uw matrix niet vierkant is of als de determinant nul is, schrijft u 'geen unieke oplossing'. Het probleem is voltooid. Als de matrix vierkant is en de bepalende factor niet nul is, gaat u door naar het volgende gedeelte voor de volgende stap: het vinden van het omgekeerde.
Tweede deel van de drie:
De matrix omkeren
-
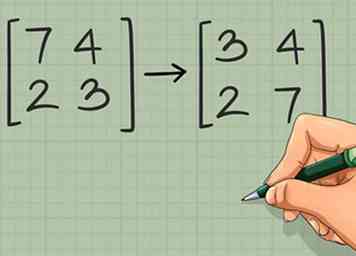 1 Zet de posities van de elementen op de hoofddiagonaal van 2 x 2. Als uw matrix 2 x 2 is, kunt u een snelkoppeling gebruiken om deze berekening veel gemakkelijker te maken.[7] De eerste stap in deze snelkoppeling bestaat uit het omwisselen van het element linksboven met het element rechtsonder. Bijvoorbeeld:
1 Zet de posities van de elementen op de hoofddiagonaal van 2 x 2. Als uw matrix 2 x 2 is, kunt u een snelkoppeling gebruiken om deze berekening veel gemakkelijker te maken.[7] De eerste stap in deze snelkoppeling bestaat uit het omwisselen van het element linksboven met het element rechtsonder. Bijvoorbeeld: - →
- Notitie: De meeste mensen gebruiken rekenmachines om het omgekeerde van een 3 x 3 matrix of groter te vinden. Als u het met de hand wilt berekenen, raadpleegt u het einde van dit gedeelte.
-
 2 Neem het tegenovergestelde van de andere twee elementen, maar laat ze in positie. Met andere woorden, vermenigvuldig de top rechts en onderaan links elementen door -1:
2 Neem het tegenovergestelde van de andere twee elementen, maar laat ze in positie. Met andere woorden, vermenigvuldig de top rechts en onderaan links elementen door -1: - →
-
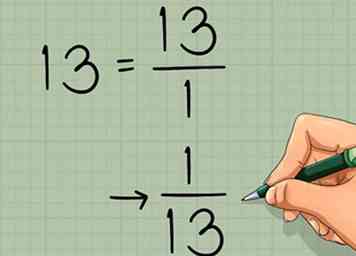 3 Neem de reciproke van de determinant. Je hebt de determinant van deze matrix gevonden in de sectie hierboven, dus het is niet nodig om het een tweede keer te berekenen. Noteer gewoon de reciproke 1 / (determinant):
3 Neem de reciproke van de determinant. Je hebt de determinant van deze matrix gevonden in de sectie hierboven, dus het is niet nodig om het een tweede keer te berekenen. Noteer gewoon de reciproke 1 / (determinant): - In ons voorbeeld is de determinant 13. Het omgekeerde hiervan is .
-
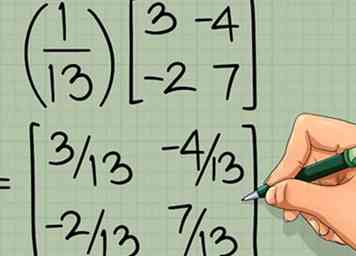 4 Vermenigvuldig de nieuwe matrix met de reciproke van de determinant. Vermenigvuldig elk element van de nieuwe matrix met het omgekeerde dat u zojuist hebt gevonden. De resulterende matrix is het omgekeerde van de 2 x 2 matrix:
4 Vermenigvuldig de nieuwe matrix met de reciproke van de determinant. Vermenigvuldig elk element van de nieuwe matrix met het omgekeerde dat u zojuist hebt gevonden. De resulterende matrix is het omgekeerde van de 2 x 2 matrix: -
=
-
-
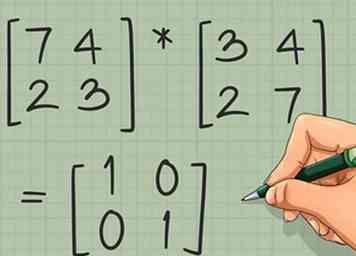 5 Controleer of de inverse correct is. Om uw werk te controleren, vermenigvuldigt u de inverse met de originele matrix. Als het omgekeerde correct is, zal hun product altijd de identiteitsmatrix zijn, Als de wiskunde uitcheckt, gaat u door naar het volgende gedeelte om uw probleem te verhelpen.
5 Controleer of de inverse correct is. Om uw werk te controleren, vermenigvuldigt u de inverse met de originele matrix. Als het omgekeerde correct is, zal hun product altijd de identiteitsmatrix zijn, Als de wiskunde uitcheckt, gaat u door naar het volgende gedeelte om uw probleem te verhelpen. - Voor het voorbeeldprobleem, vermenigvuldig .
- Hier volgt een opfriscursus over het vermenigvuldigen van matrices.
- Opmerking: Matrixvermenigvuldiging is niet commutatief: de volgorde van de factoren is van belang. Wanneer een matrix echter wordt vermenigvuldigd met zijn inverse, zullen beide opties resulteren in de identiteitsmatrix.[8]
-
 6 Herzie matrixinversie voor 3 x 3 matrices of groter. Tenzij u dit proces voor de eerste keer leert, kunt u tijd besparen door een grafische rekenmachine of wiskundige software te gebruiken voor grotere matrices. Als u dit handmatig moet berekenen, vindt u hier een korte samenvatting van één methode:[9][10]
6 Herzie matrixinversie voor 3 x 3 matrices of groter. Tenzij u dit proces voor de eerste keer leert, kunt u tijd besparen door een grafische rekenmachine of wiskundige software te gebruiken voor grotere matrices. Als u dit handmatig moet berekenen, vindt u hier een korte samenvatting van één methode:[9][10] - Voeg de identiteitsmatrix I toe aan de rechterkant van uw matrix. Bijvoorbeeld [B] → [B | I]. De identiteitsmatrix heeft "1" -elementen langs de hoofddiagonaal en "0" -elementen in alle andere posities.
- Voer rijbewerkingen uit om de matrix te verkleinen totdat de linkerkant zich in de rij-echelonvorm bevindt en verminder vervolgens totdat de linkerkant de identiteitsmatrix is.
- Zodra de bewerking is voltooid, heeft uw matrix de vorm [I | B-1]. Met andere woorden, de rechterkant zal het omgekeerde zijn van de originele matrix.
Derde deel van de drie:
Matrixen vermenigvuldigen om het probleem te voltooien
-
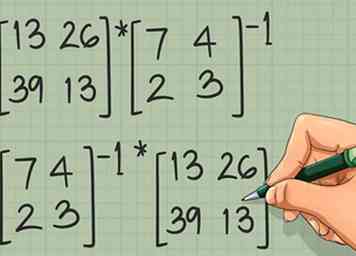 1 Schrijf beide mogelijke vergelijkingen. In "gewone wiskunde" met scalaire grootheden is vermenigvuldiging commutatief; 2 x 6 = 6 x 2. Dit is niet waar voor matrices, dus u moet mogelijk twee problemen oplossen:
1 Schrijf beide mogelijke vergelijkingen. In "gewone wiskunde" met scalaire grootheden is vermenigvuldiging commutatief; 2 x 6 = 6 x 2. Dit is niet waar voor matrices, dus u moet mogelijk twee problemen oplossen: - [A] * [B]-1 is de oplossing X voor het probleem X[B] = [A].
- [B]-1 * [A] is de oplossing X voor het probleem [B]X = [A].
- Als dit deel uitmaakt van een vergelijking, zorg er dan voor dat u aan beide kanten dezelfde bewerking uitvoert. Als [A] = [C], dan [B]-1[A] doet niet gelijk [C] [B]-1, omdat de [B]-1 bevindt zich aan de linkerkant van [A], maar aan de rechterkant van [C].[11]
-
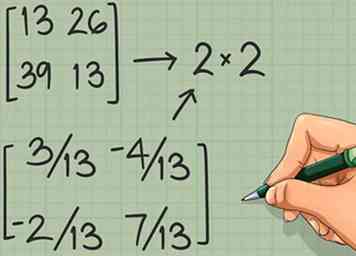 2 Zoek de dimensies van uw antwoord. De afmetingen van de uiteindelijke matrix zijn de buitenste dimensies van de twee factoren. Het heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix.
2 Zoek de dimensies van uw antwoord. De afmetingen van de uiteindelijke matrix zijn de buitenste dimensies van de twee factoren. Het heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. - Terugkeren naar ons oorspronkelijke voorbeeld, beide en zijn 2 x 2 matrices, dus de afmetingen van het antwoord zijn ook 2 x 2.
- Om een meer gecompliceerd voorbeeld te nemen, als [A] een is 4 x 3 matrix en [B]-1 is een 3 x 3 matrix en vervolgens de matrix [A] * [B]-1 heeft afmetingen van 4 x 3.
-
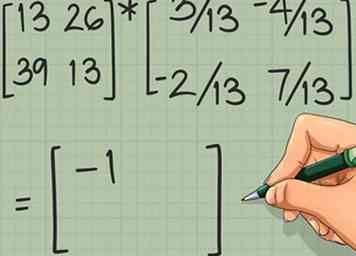 3 Zoek de waarde van het eerste element. Raadpleeg het gelinkte artikel voor volledige instructies of vernieuw uw geheugen met deze samenvatting:
3 Zoek de waarde van het eerste element. Raadpleeg het gelinkte artikel voor volledige instructies of vernieuw uw geheugen met deze samenvatting: - Om rij 1, kolom 1 van [A] [B] te vinden-1, vind het puntproduct van [A] rij 1 en [B]-1 kolom 1. Dat wil zeggen, voor een 2 x 2 matrix, berekenen .
- In ons voorbeeld , rij 1, kolom 1 van ons antwoord is:
-
 4 Herhaal het proces van het puntproduct voor elke positie in uw matrix. Het element op positie 2,1 is bijvoorbeeld het puntproduct van [A] rij 2 en [B]-1 kolom 1. Probeer het voorbeeld zelf te voltooien. Je zou de volgende antwoorden moeten krijgen:
4 Herhaal het proces van het puntproduct voor elke positie in uw matrix. Het element op positie 2,1 is bijvoorbeeld het puntproduct van [A] rij 2 en [B]-1 kolom 1. Probeer het voorbeeld zelf te voltooien. Je zou de volgende antwoorden moeten krijgen: - Als je de andere oplossing moet vinden,
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
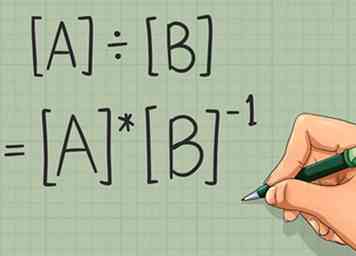 1 Begrijp matrix "verdeling." Technisch gezien bestaat er niet zoiets als matrixverdeling. Het verdelen van een matrix door een andere matrix is een ongedefinieerde functie.[2] Het dichtstbijzijnde equivalent vermenigvuldigt zich met de inverse van een andere matrix. Met andere woorden, terwijl [A] ÷ [B] niet is gedefinieerd, kunt u het probleem oplossen [A] * [B]-1. Aangezien deze twee vergelijkingen hetzelfde zouden zijn voor scalaire grootheden, voelt dit als matrixverdeling, maar het is belangrijk om de juiste terminologie te gebruiken.
1 Begrijp matrix "verdeling." Technisch gezien bestaat er niet zoiets als matrixverdeling. Het verdelen van een matrix door een andere matrix is een ongedefinieerde functie.[2] Het dichtstbijzijnde equivalent vermenigvuldigt zich met de inverse van een andere matrix. Met andere woorden, terwijl [A] ÷ [B] niet is gedefinieerd, kunt u het probleem oplossen [A] * [B]-1. Aangezien deze twee vergelijkingen hetzelfde zouden zijn voor scalaire grootheden, voelt dit als matrixverdeling, maar het is belangrijk om de juiste terminologie te gebruiken. 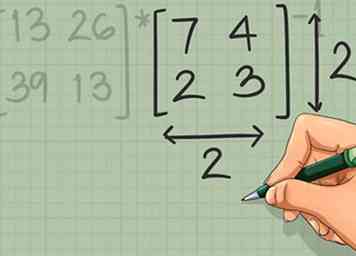 2 Bevestig dat de "delermatrix" vierkant is. Om de inverse van een matrix te nemen, moet deze een vierkante matrix zijn met hetzelfde aantal rijen en kolommen. Als de matrix die u van plan bent te omkeren niet-vierkant is, is er geen unieke oplossing voor het probleem.[3]
2 Bevestig dat de "delermatrix" vierkant is. Om de inverse van een matrix te nemen, moet deze een vierkante matrix zijn met hetzelfde aantal rijen en kolommen. Als de matrix die u van plan bent te omkeren niet-vierkant is, is er geen unieke oplossing voor het probleem.[3] 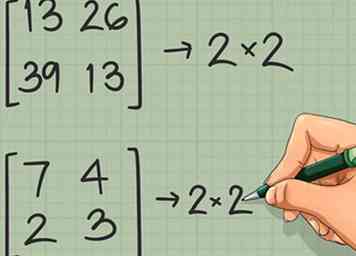 3 Controleer of de twee matrices samen kunnen worden vermenigvuldigd. Om twee matrices samen te vermenigvuldigen, moet het aantal kolommen in de eerste matrix gelijk zijn aan het aantal rijen in de tweede matrix.[4] Als dit niet werkt in beide regelingen ([A] * [B]-1 of [B]-1 * [A]), er is geen oplossing voor het probleem.
3 Controleer of de twee matrices samen kunnen worden vermenigvuldigd. Om twee matrices samen te vermenigvuldigen, moet het aantal kolommen in de eerste matrix gelijk zijn aan het aantal rijen in de tweede matrix.[4] Als dit niet werkt in beide regelingen ([A] * [B]-1 of [B]-1 * [A]), er is geen oplossing voor het probleem. 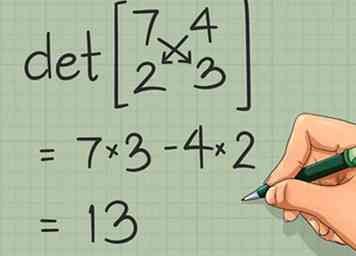 4 Zoek de determinant van een matrix van 2 x 2. Er is nog een vereiste om te controleren voordat u de inverse van een matrix kunt nemen. De determinant van de matrix moet niet-nul zijn. Als de determinant nul is, heeft de matrix geen inverse. U kunt de determinant in het eenvoudigste geval als de 2 x 2 matrix vinden:
4 Zoek de determinant van een matrix van 2 x 2. Er is nog een vereiste om te controleren voordat u de inverse van een matrix kunt nemen. De determinant van de matrix moet niet-nul zijn. Als de determinant nul is, heeft de matrix geen inverse. U kunt de determinant in het eenvoudigste geval als de 2 x 2 matrix vinden: 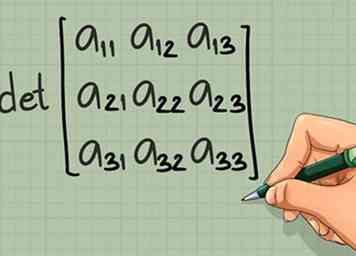 5 Zoek de determinant van een grotere matrix. Als uw matrix 3 x 3 of groter is, kost het vinden van de determinant wat meer werk:
5 Zoek de determinant van een grotere matrix. Als uw matrix 3 x 3 of groter is, kost het vinden van de determinant wat meer werk: 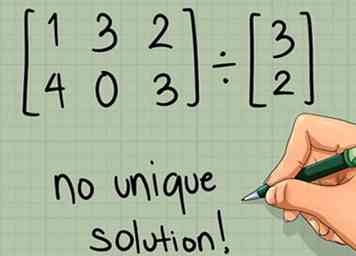 6 Ga door. Als uw matrix niet vierkant is of als de determinant nul is, schrijft u 'geen unieke oplossing'. Het probleem is voltooid. Als de matrix vierkant is en de bepalende factor niet nul is, gaat u door naar het volgende gedeelte voor de volgende stap: het vinden van het omgekeerde.
6 Ga door. Als uw matrix niet vierkant is of als de determinant nul is, schrijft u 'geen unieke oplossing'. Het probleem is voltooid. Als de matrix vierkant is en de bepalende factor niet nul is, gaat u door naar het volgende gedeelte voor de volgende stap: het vinden van het omgekeerde. 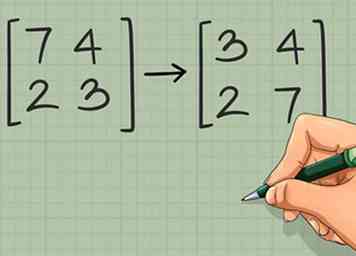 1 Zet de posities van de elementen op de hoofddiagonaal van 2 x 2. Als uw matrix 2 x 2 is, kunt u een snelkoppeling gebruiken om deze berekening veel gemakkelijker te maken.[7] De eerste stap in deze snelkoppeling bestaat uit het omwisselen van het element linksboven met het element rechtsonder. Bijvoorbeeld:
1 Zet de posities van de elementen op de hoofddiagonaal van 2 x 2. Als uw matrix 2 x 2 is, kunt u een snelkoppeling gebruiken om deze berekening veel gemakkelijker te maken.[7] De eerste stap in deze snelkoppeling bestaat uit het omwisselen van het element linksboven met het element rechtsonder. Bijvoorbeeld:  2 Neem het tegenovergestelde van de andere twee elementen, maar laat ze in positie. Met andere woorden, vermenigvuldig de top rechts en onderaan links elementen door -1:
2 Neem het tegenovergestelde van de andere twee elementen, maar laat ze in positie. Met andere woorden, vermenigvuldig de top rechts en onderaan links elementen door -1: 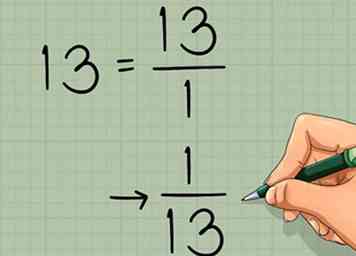 3 Neem de reciproke van de determinant. Je hebt de determinant van deze matrix gevonden in de sectie hierboven, dus het is niet nodig om het een tweede keer te berekenen. Noteer gewoon de reciproke 1 / (determinant):
3 Neem de reciproke van de determinant. Je hebt de determinant van deze matrix gevonden in de sectie hierboven, dus het is niet nodig om het een tweede keer te berekenen. Noteer gewoon de reciproke 1 / (determinant): 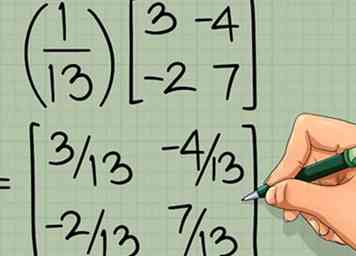 4 Vermenigvuldig de nieuwe matrix met de reciproke van de determinant. Vermenigvuldig elk element van de nieuwe matrix met het omgekeerde dat u zojuist hebt gevonden. De resulterende matrix is het omgekeerde van de 2 x 2 matrix:
4 Vermenigvuldig de nieuwe matrix met de reciproke van de determinant. Vermenigvuldig elk element van de nieuwe matrix met het omgekeerde dat u zojuist hebt gevonden. De resulterende matrix is het omgekeerde van de 2 x 2 matrix: 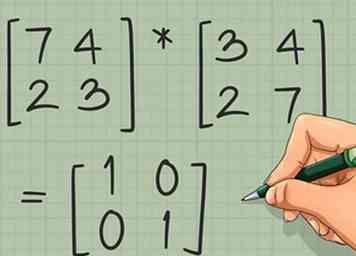 5 Controleer of de inverse correct is. Om uw werk te controleren, vermenigvuldigt u de inverse met de originele matrix. Als het omgekeerde correct is, zal hun product altijd de identiteitsmatrix zijn,
5 Controleer of de inverse correct is. Om uw werk te controleren, vermenigvuldigt u de inverse met de originele matrix. Als het omgekeerde correct is, zal hun product altijd de identiteitsmatrix zijn,  6 Herzie matrixinversie voor 3 x 3 matrices of groter. Tenzij u dit proces voor de eerste keer leert, kunt u tijd besparen door een grafische rekenmachine of wiskundige software te gebruiken voor grotere matrices. Als u dit handmatig moet berekenen, vindt u hier een korte samenvatting van één methode:[9][10]
6 Herzie matrixinversie voor 3 x 3 matrices of groter. Tenzij u dit proces voor de eerste keer leert, kunt u tijd besparen door een grafische rekenmachine of wiskundige software te gebruiken voor grotere matrices. Als u dit handmatig moet berekenen, vindt u hier een korte samenvatting van één methode:[9][10] 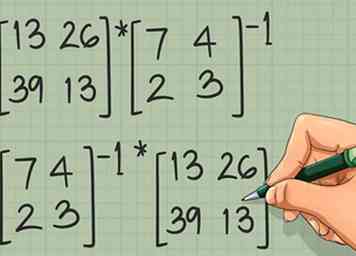 1 Schrijf beide mogelijke vergelijkingen. In "gewone wiskunde" met scalaire grootheden is vermenigvuldiging commutatief; 2 x 6 = 6 x 2. Dit is niet waar voor matrices, dus u moet mogelijk twee problemen oplossen:
1 Schrijf beide mogelijke vergelijkingen. In "gewone wiskunde" met scalaire grootheden is vermenigvuldiging commutatief; 2 x 6 = 6 x 2. Dit is niet waar voor matrices, dus u moet mogelijk twee problemen oplossen: 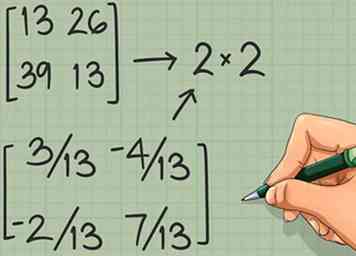 2 Zoek de dimensies van uw antwoord. De afmetingen van de uiteindelijke matrix zijn de buitenste dimensies van de twee factoren. Het heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix.
2 Zoek de dimensies van uw antwoord. De afmetingen van de uiteindelijke matrix zijn de buitenste dimensies van de twee factoren. Het heeft hetzelfde aantal rijen als de eerste matrix en hetzelfde aantal kolommen als de tweede matrix. 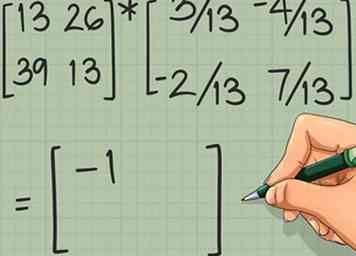 3 Zoek de waarde van het eerste element. Raadpleeg het gelinkte artikel voor volledige instructies of vernieuw uw geheugen met deze samenvatting:
3 Zoek de waarde van het eerste element. Raadpleeg het gelinkte artikel voor volledige instructies of vernieuw uw geheugen met deze samenvatting:  4 Herhaal het proces van het puntproduct voor elke positie in uw matrix. Het element op positie 2,1 is bijvoorbeeld het puntproduct van [A] rij 2 en [B]-1 kolom 1. Probeer het voorbeeld zelf te voltooien. Je zou de volgende antwoorden moeten krijgen:
4 Herhaal het proces van het puntproduct voor elke positie in uw matrix. Het element op positie 2,1 is bijvoorbeeld het puntproduct van [A] rij 2 en [B]-1 kolom 1. Probeer het voorbeeld zelf te voltooien. Je zou de volgende antwoorden moeten krijgen: