Een rekenkundige reeks is een lijst met getallen die van de een naar de ander verschillen door een constante hoeveelheid. Bijvoorbeeld de lijst met even nummers, ... is een rekenkundige reeks, omdat het verschil tussen het ene getal in de lijst en het volgende altijd 2 is. Als u weet dat u met een rekenkundige reeks werkt, wordt u mogelijk gevraagd de volgende term uit een gegeven lijst te vinden. Mogelijk wordt u ook gevraagd een gat in te vullen waar een term ontbreekt. Als laatste zou je bijvoorbeeld de 100e termijn willen weten, zonder feitelijk alle 100 termen uit te schrijven. Een paar eenvoudige stappen kunnen u helpen een van deze te doen.
Methode één van de vier:
De volgende term vinden in een rekenkundige reeks
-
 1 Zoek het gemeenschappelijke verschil voor de reeks. Wanneer u een lijst met getallen te zien krijgt, wordt u mogelijk verteld dat de lijst een rekenkundige reeks is, of u moet dit misschien zelf uitvogelen. De eerste stap is in beide gevallen hetzelfde. Selecteer de eerste twee opeenvolgende termen in de lijst. Trek de eerste term van de tweede term af. Het resultaat is het gemeenschappelijke verschil van uw reeks.[1]
1 Zoek het gemeenschappelijke verschil voor de reeks. Wanneer u een lijst met getallen te zien krijgt, wordt u mogelijk verteld dat de lijst een rekenkundige reeks is, of u moet dit misschien zelf uitvogelen. De eerste stap is in beide gevallen hetzelfde. Selecteer de eerste twee opeenvolgende termen in de lijst. Trek de eerste term van de tweede term af. Het resultaat is het gemeenschappelijke verschil van uw reeks.[1] - Stel dat u de lijst hebt ... Trek af om het gemeenschappelijke verschil van 3 te vinden.
- Stel dat u een lijst met termen hebt die afneemt, zoals .... Je trekt nog steeds de eerste term van de tweede af om het verschil te vinden. In dit geval, dat geeft jou . Het negatieve resultaat betekent dat uw lijst afneemt terwijl u van links naar rechts leest. Je moet altijd controleren of het teken van het verschil overeenkomt met de richting waarin de cijfers lijken te gaan.
-
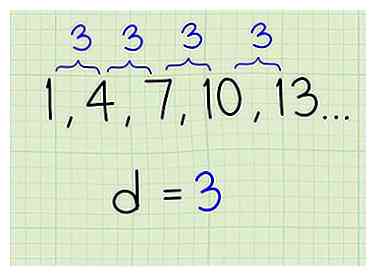 2 Controleer of het gemeenschappelijke verschil consistent is. Het vinden van het gemeenschappelijke verschil voor alleen de eerste twee termen zorgt er niet voor dat uw lijst een rekenkundige reeks is. U moet ervoor zorgen dat het verschil consistent is voor de hele lijst. Controleer het verschil door twee verschillende opeenvolgende termen in de lijst af te trekken. Als het resultaat consistent is voor een of twee andere termen, heb je waarschijnlijk een rekenkundige reeks.
2 Controleer of het gemeenschappelijke verschil consistent is. Het vinden van het gemeenschappelijke verschil voor alleen de eerste twee termen zorgt er niet voor dat uw lijst een rekenkundige reeks is. U moet ervoor zorgen dat het verschil consistent is voor de hele lijst. Controleer het verschil door twee verschillende opeenvolgende termen in de lijst af te trekken. Als het resultaat consistent is voor een of twee andere termen, heb je waarschijnlijk een rekenkundige reeks. - Werken met hetzelfde voorbeeld, ... kies de tweede en derde voorwaarde van de lijst. Aftrekken en je merkt dat het verschil nog steeds 3 is. Om te bevestigen, nog een voorbeeld controleren en aftrekken , en je merkt dat het verschil consistent 3 is. Je kunt er vrij zeker van zijn dat je met een rekenkundige reeks werkt.
- Het is mogelijk dat een lijst met getallen een rekenkundige reeks lijkt op basis van de eerste paar termen, maar daarna mislukt. Bekijk bijvoorbeeld de lijst .... Het verschil tussen de eerste en tweede termen is 1 en het verschil tussen de tweede en derde term is ook 1. Het verschil tussen de derde en vierde voorwaarde is echter 3. Omdat het verschil niet gebruikelijk is voor de volledige lijst, is dit is geen rekenkundige reeks.
-
 3 Voeg het algemene verschil toe aan de laatst opgegeven term. Het vinden van de volgende termijn van een rekenkundige reeks nadat u het gemeenschappelijke verschil kent, is eenvoudig. Voeg gewoon het algemene verschil toe aan de laatste term van de lijst en u krijgt het volgende nummer.
3 Voeg het algemene verschil toe aan de laatst opgegeven term. Het vinden van de volgende termijn van een rekenkundige reeks nadat u het gemeenschappelijke verschil kent, is eenvoudig. Voeg gewoon het algemene verschil toe aan de laatste term van de lijst en u krijgt het volgende nummer. - Bijvoorbeeld in het voorbeeld van ..., om het volgende nummer in de lijst te vinden, voegt u het gemeenschappelijke verschil van 3 toe aan de laatst opgegeven term. Het toevoegen resultaten in 16, wat de volgende term is. Je kunt doorgaan met het toevoegen van 3 om je lijst zo lang te maken als je wilt. De lijst zou bijvoorbeeld zijn .... Je kunt dit zo lang doen als je wilt.
Methode twee van vier:
Een ontbrekende interne term vinden
-
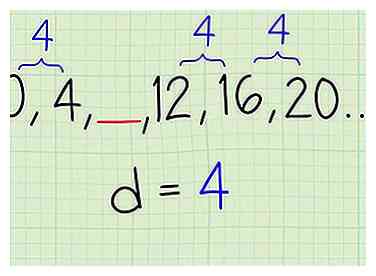 1 Controleer of u begint met een rekenkundige reeks. In sommige gevallen heb je misschien een lijst met nummers met een ontbrekende term in het midden. Begin, zoals eerder, door te controleren of uw lijst een rekenkundige reeks is. Selecteer twee willekeurige opeenvolgende termen en vind het verschil ertussen. Controleer dit vervolgens tegen twee andere opeenvolgende termen in de lijst. Als de verschillen hetzelfde zijn, kunt u ervan uitgaan dat u met een rekenkundige reeks werkt en verdergaat.
1 Controleer of u begint met een rekenkundige reeks. In sommige gevallen heb je misschien een lijst met nummers met een ontbrekende term in het midden. Begin, zoals eerder, door te controleren of uw lijst een rekenkundige reeks is. Selecteer twee willekeurige opeenvolgende termen en vind het verschil ertussen. Controleer dit vervolgens tegen twee andere opeenvolgende termen in de lijst. Als de verschillen hetzelfde zijn, kunt u ervan uitgaan dat u met een rekenkundige reeks werkt en verdergaat. - Stel dat u de lijst hebt ,___,.... Begin met aftrekken om een verschil van 4 te vinden. Controleer dit tegen twee andere opeenvolgende termen, zoals . Het verschil is weer 4. Je kunt doorgaan.
-
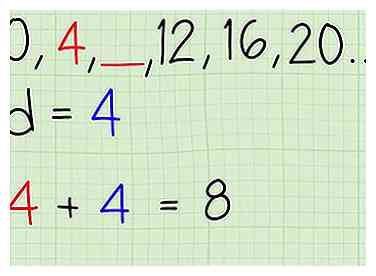 2 Voeg het algemene verschil toe aan de term vóór de spatie. Dit lijkt op het toevoegen van een term aan het einde van een reeks. Zoek de term die onmiddellijk voorafgaat aan de spatie in uw reeks. Dit is het "laatste" nummer dat u kent. Voeg uw algemene verschil toe aan deze term om het nummer te vinden dat de spatie moet invullen.
2 Voeg het algemene verschil toe aan de term vóór de spatie. Dit lijkt op het toevoegen van een term aan het einde van een reeks. Zoek de term die onmiddellijk voorafgaat aan de spatie in uw reeks. Dit is het "laatste" nummer dat u kent. Voeg uw algemene verschil toe aan deze term om het nummer te vinden dat de spatie moet invullen. - In ons werkvoorbeeld, ,____,..., de term die voorafgaat aan de spatie is 4, en ons gemeenschappelijk verschil voor deze lijst is ook 4. Dus voeg toe om 8 te krijgen, wat het nummer in de lege ruimte zou moeten zijn.
-
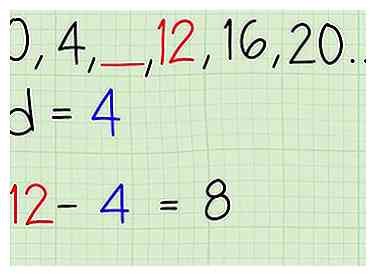 3 Trek het algemene verschil af van de term die volgt op de spatie. Controleer de andere richting om er zeker van te zijn dat u het juiste antwoord krijgt. Een rekenkundige reeks moet consistent zijn in beide richtingen.Als je van links naar rechts beweegt en 4 optelt, en dan in de tegenovergestelde richting, van rechts naar links, zou je het tegenovergestelde doen en 4 aftrekken.
3 Trek het algemene verschil af van de term die volgt op de spatie. Controleer de andere richting om er zeker van te zijn dat u het juiste antwoord krijgt. Een rekenkundige reeks moet consistent zijn in beide richtingen.Als je van links naar rechts beweegt en 4 optelt, en dan in de tegenovergestelde richting, van rechts naar links, zou je het tegenovergestelde doen en 4 aftrekken. - In het werkvoorbeeld, ,___,..., de term onmiddellijk volgend op de spatie is 12. Trek het gemeenschappelijke verschil van 4 van deze term af om te vinden . Het resultaat van 8 moet de lege ruimte invullen.
-
 4 Vergelijk uw resultaten. De twee resultaten die u krijgt, van optellen vanaf de bodem of van het aftrekken van de bovenkant moeten overeenkomen. Als dat het geval is, hebt u de waarde voor de ontbrekende term gevonden. Als dat niet het geval is, moet u uw werk controleren. Mogelijk hebt u geen echte rekenkundige reeks.
4 Vergelijk uw resultaten. De twee resultaten die u krijgt, van optellen vanaf de bodem of van het aftrekken van de bovenkant moeten overeenkomen. Als dat het geval is, hebt u de waarde voor de ontbrekende term gevonden. Als dat niet het geval is, moet u uw werk controleren. Mogelijk hebt u geen echte rekenkundige reeks. - In het werkvoorbeeld zijn de twee resultaten van en beide gaven de oplossing van 8. Daarom is de ontbrekende term in deze rekenkundige reeks 8. De volledige sequentie is … .
Methode drie van vier:
De N-de termijn van een rekenkundige reeks vinden
-
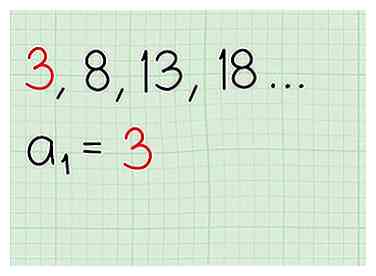 1 Identificeer de eerste termijn van de reeks. Niet elke reeks begint met de cijfers 0 of 1. Bekijk de lijst met nummers die u hebt en zoek de eerste term. Dit is uw startpunt, dat kan worden aangewezen met behulp van variabelen als (1).
1 Identificeer de eerste termijn van de reeks. Niet elke reeks begint met de cijfers 0 of 1. Bekijk de lijst met nummers die u hebt en zoek de eerste term. Dit is uw startpunt, dat kan worden aangewezen met behulp van variabelen als (1). - Het is gebruikelijk om met aritmetische reeksen de variabele a (1) te gebruiken om de eerste term van een reeks aan te duiden. U kunt natuurlijk elke gewenste variabele kiezen en de resultaten moeten hetzelfde zijn.
- Bijvoorbeeld, gezien de reeks ..., de eerste term is , die algebraïsch als een (1) kan worden aangeduid.
-
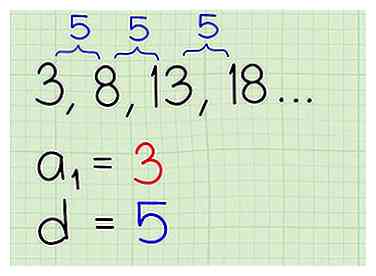 2 Definieer je gemeenschappelijke verschil als d. Zoek het gemeenschappelijke verschil voor de reeks zoals eerder. In dit werkvoorbeeld is het gemeenschappelijke verschil , wat 5 is. Het controleren met andere termen in de reeks levert hetzelfde resultaat op. We zullen dit gemeenschappelijke verschil met de algebraïsche variabele d opmerken.
2 Definieer je gemeenschappelijke verschil als d. Zoek het gemeenschappelijke verschil voor de reeks zoals eerder. In dit werkvoorbeeld is het gemeenschappelijke verschil , wat 5 is. Het controleren met andere termen in de reeks levert hetzelfde resultaat op. We zullen dit gemeenschappelijke verschil met de algebraïsche variabele d opmerken. -
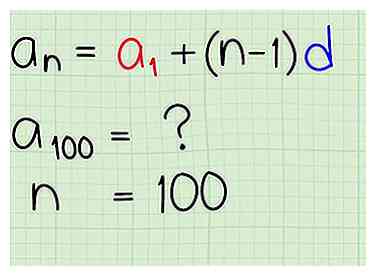 3 Gebruik de expliciete formule. Een expliciete formule is een algebraïsche vergelijking die u kunt gebruiken om een willekeurige rij van een rekenkundige reeks te vinden, zonder dat u de volledige lijst hoeft te schrijven. De expliciete formule voor een algebraïsche sequentie is .
3 Gebruik de expliciete formule. Een expliciete formule is een algebraïsche vergelijking die u kunt gebruiken om een willekeurige rij van een rekenkundige reeks te vinden, zonder dat u de volledige lijst hoeft te schrijven. De expliciete formule voor een algebraïsche sequentie is . - De term a (n) kan worden gelezen als "de n-de term van a", waarbij n staat voor welk nummer in de lijst die u wilt vinden en een (n) de werkelijke waarde van dat getal is. Als u bijvoorbeeld wordt gevraagd het 100ste item in een rekenkundige reeks te vinden, is n 100. In dit voorbeeld is n 100, maar a (n) is de waarde van de 100e term, niet het getal 100 zelf.
-
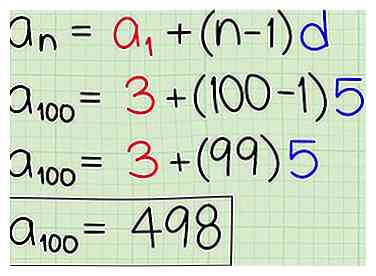 4 Vul uw gegevens in om het probleem op te lossen. Gebruik de expliciete formule voor uw reeks en vul de informatie in die u kent om de term te vinden die u nodig hebt.
4 Vul uw gegevens in om het probleem op te lossen. Gebruik de expliciete formule voor uw reeks en vul de informatie in die u kent om de term te vinden die u nodig hebt. - Bijvoorbeeld in het werkvoorbeeld ..., we weten dat a (1) de eerste term 3 is, en het gemeenschappelijke verschil d is 5. Stel dat je gevraagd wordt om de 100e term in die volgorde te vinden. Dan is n = 100 en (n-1) = 99. De volledige expliciete formule, met de ingevulde gegevens, is dan . Dit vereenvoudigt tot 498, wat de 100e term is van die reeks.
Methode vier van vier:
De expliciete formule gebruiken om aanvullende informatie te zoeken
-
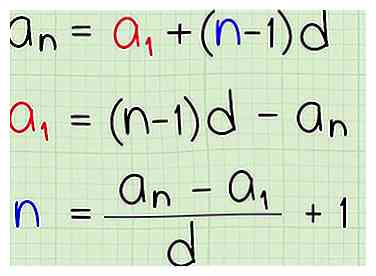 1 Herschik de expliciete formule om op te lossen voor andere variabelen. Met behulp van de expliciete formule en enkele basisalgebra kun je verschillende stukjes informatie over een rekenkundige reeks vinden. In de oorspronkelijke vorm, , de expliciete formule is ontworpen om op te lossen voor eenn en geef je de nde termijn van een reeks. U kunt deze formule echter algebraïsch manipuleren en oplossen voor een van de variabelen.
1 Herschik de expliciete formule om op te lossen voor andere variabelen. Met behulp van de expliciete formule en enkele basisalgebra kun je verschillende stukjes informatie over een rekenkundige reeks vinden. In de oorspronkelijke vorm, , de expliciete formule is ontworpen om op te lossen voor eenn en geef je de nde termijn van een reeks. U kunt deze formule echter algebraïsch manipuleren en oplossen voor een van de variabelen. - Stel dat u het einde van een lijst met getallen hebt, maar u moet weten wat het begin van de reeks was. U kunt de formule opnieuw rangschikken om u te geven
- Als u het beginpunt van een rekenkundige reeks en het eindpunt kent, maar u moet weten hoeveel termen in de lijst staan, dan kunt u de expliciete formule om op te lossen voor n herschikken. Dit zou zijn .
- Als je de basisregels van de algebra moet herzien om dit resultaat te maken, ga je naar Algebra doen of Algebraïsche uitdrukkingen vereenvoudigen.
-
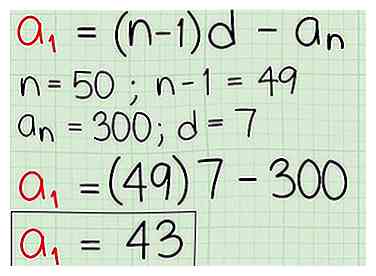 2 Zoek de eerste term van een reeks. Je weet misschien dat de 50e termijn van een rekenkundige reeks 300 is, en je weet dat de termen met 7 zijn toegenomen (het "gemeenschappelijke verschil"), maar je wilt weten wat de eerste term van de reeks was. Gebruik de herziene expliciete formule die lost voor a1 om uw antwoord te vinden.
2 Zoek de eerste term van een reeks. Je weet misschien dat de 50e termijn van een rekenkundige reeks 300 is, en je weet dat de termen met 7 zijn toegenomen (het "gemeenschappelijke verschil"), maar je wilt weten wat de eerste term van de reeks was. Gebruik de herziene expliciete formule die lost voor a1 om uw antwoord te vinden. - Gebruik de vergelijking en vul de informatie in die u kent. Omdat je weet dat de 50e termijn 300 is, dan is n = 50, n-1 = 49 en a (n) = 300. Je krijgt ook dat het gemeenschappelijke verschil, d, is 7. Daarom wordt de formule . Dit komt uit naar . De reeks die je hebt begonnen bij 43, en geteld met 7. Daarom lijkt het 43,50,57,64,71,78 ... 293,300.
-
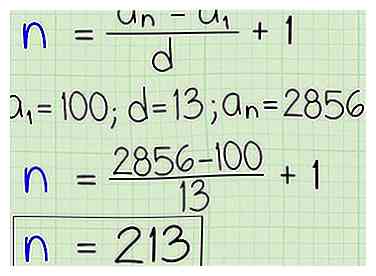 3 Zoek de lengte van een reeks. Stel dat je alles weet over het begin en einde van een rekenkundige reeks, maar je moet weten hoe lang het is. Gebruik de herziene formule .
3 Zoek de lengte van een reeks. Stel dat je alles weet over het begin en einde van een rekenkundige reeks, maar je moet weten hoe lang het is. Gebruik de herziene formule . - Stel dat je weet dat een gegeven rekenkundige reeks begint bij 100 en toeneemt met 13. Je krijgt ook te horen dat de laatste term 2.856 is. Gebruik de termen a1 = 100, d = 13 en a (n) = 2856 om de lengte van de reeks te vinden. Voeg deze termen toe aan de te geven formule . Als je dit uitwerkt, krijg je , wat gelijk is aan 212 + 1, wat 213 is. Er zijn 213 termen in die reeks.
- Deze voorbeeldsequentie zou er uitzien als 100, 113, 126, 139 ... 2843, 2856.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Zoek het gemeenschappelijke verschil voor de reeks. Wanneer u een lijst met getallen te zien krijgt, wordt u mogelijk verteld dat de lijst een rekenkundige reeks is, of u moet dit misschien zelf uitvogelen. De eerste stap is in beide gevallen hetzelfde. Selecteer de eerste twee opeenvolgende termen in de lijst. Trek de eerste term van de tweede term af. Het resultaat is het gemeenschappelijke verschil van uw reeks.[1]
1 Zoek het gemeenschappelijke verschil voor de reeks. Wanneer u een lijst met getallen te zien krijgt, wordt u mogelijk verteld dat de lijst een rekenkundige reeks is, of u moet dit misschien zelf uitvogelen. De eerste stap is in beide gevallen hetzelfde. Selecteer de eerste twee opeenvolgende termen in de lijst. Trek de eerste term van de tweede term af. Het resultaat is het gemeenschappelijke verschil van uw reeks.[1] 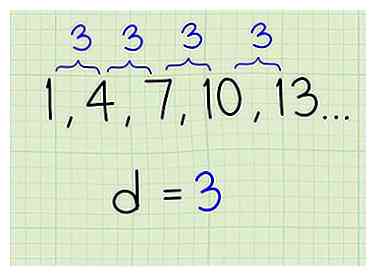 2 Controleer of het gemeenschappelijke verschil consistent is. Het vinden van het gemeenschappelijke verschil voor alleen de eerste twee termen zorgt er niet voor dat uw lijst een rekenkundige reeks is. U moet ervoor zorgen dat het verschil consistent is voor de hele lijst. Controleer het verschil door twee verschillende opeenvolgende termen in de lijst af te trekken. Als het resultaat consistent is voor een of twee andere termen, heb je waarschijnlijk een rekenkundige reeks.
2 Controleer of het gemeenschappelijke verschil consistent is. Het vinden van het gemeenschappelijke verschil voor alleen de eerste twee termen zorgt er niet voor dat uw lijst een rekenkundige reeks is. U moet ervoor zorgen dat het verschil consistent is voor de hele lijst. Controleer het verschil door twee verschillende opeenvolgende termen in de lijst af te trekken. Als het resultaat consistent is voor een of twee andere termen, heb je waarschijnlijk een rekenkundige reeks.  3 Voeg het algemene verschil toe aan de laatst opgegeven term. Het vinden van de volgende termijn van een rekenkundige reeks nadat u het gemeenschappelijke verschil kent, is eenvoudig. Voeg gewoon het algemene verschil toe aan de laatste term van de lijst en u krijgt het volgende nummer.
3 Voeg het algemene verschil toe aan de laatst opgegeven term. Het vinden van de volgende termijn van een rekenkundige reeks nadat u het gemeenschappelijke verschil kent, is eenvoudig. Voeg gewoon het algemene verschil toe aan de laatste term van de lijst en u krijgt het volgende nummer. 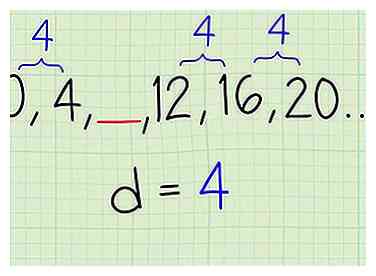 1 Controleer of u begint met een rekenkundige reeks. In sommige gevallen heb je misschien een lijst met nummers met een ontbrekende term in het midden. Begin, zoals eerder, door te controleren of uw lijst een rekenkundige reeks is. Selecteer twee willekeurige opeenvolgende termen en vind het verschil ertussen. Controleer dit vervolgens tegen twee andere opeenvolgende termen in de lijst. Als de verschillen hetzelfde zijn, kunt u ervan uitgaan dat u met een rekenkundige reeks werkt en verdergaat.
1 Controleer of u begint met een rekenkundige reeks. In sommige gevallen heb je misschien een lijst met nummers met een ontbrekende term in het midden. Begin, zoals eerder, door te controleren of uw lijst een rekenkundige reeks is. Selecteer twee willekeurige opeenvolgende termen en vind het verschil ertussen. Controleer dit vervolgens tegen twee andere opeenvolgende termen in de lijst. Als de verschillen hetzelfde zijn, kunt u ervan uitgaan dat u met een rekenkundige reeks werkt en verdergaat. 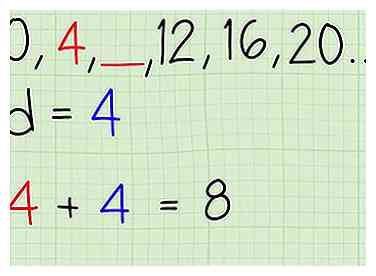 2 Voeg het algemene verschil toe aan de term vóór de spatie. Dit lijkt op het toevoegen van een term aan het einde van een reeks. Zoek de term die onmiddellijk voorafgaat aan de spatie in uw reeks. Dit is het "laatste" nummer dat u kent. Voeg uw algemene verschil toe aan deze term om het nummer te vinden dat de spatie moet invullen.
2 Voeg het algemene verschil toe aan de term vóór de spatie. Dit lijkt op het toevoegen van een term aan het einde van een reeks. Zoek de term die onmiddellijk voorafgaat aan de spatie in uw reeks. Dit is het "laatste" nummer dat u kent. Voeg uw algemene verschil toe aan deze term om het nummer te vinden dat de spatie moet invullen. 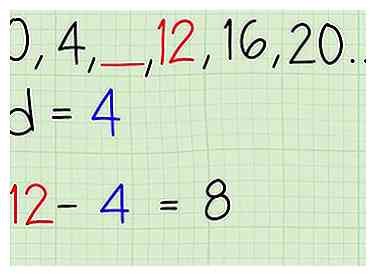 3 Trek het algemene verschil af van de term die volgt op de spatie. Controleer de andere richting om er zeker van te zijn dat u het juiste antwoord krijgt. Een rekenkundige reeks moet consistent zijn in beide richtingen.Als je van links naar rechts beweegt en 4 optelt, en dan in de tegenovergestelde richting, van rechts naar links, zou je het tegenovergestelde doen en 4 aftrekken.
3 Trek het algemene verschil af van de term die volgt op de spatie. Controleer de andere richting om er zeker van te zijn dat u het juiste antwoord krijgt. Een rekenkundige reeks moet consistent zijn in beide richtingen.Als je van links naar rechts beweegt en 4 optelt, en dan in de tegenovergestelde richting, van rechts naar links, zou je het tegenovergestelde doen en 4 aftrekken.  4 Vergelijk uw resultaten. De twee resultaten die u krijgt, van optellen vanaf de bodem of van het aftrekken van de bovenkant moeten overeenkomen. Als dat het geval is, hebt u de waarde voor de ontbrekende term gevonden. Als dat niet het geval is, moet u uw werk controleren. Mogelijk hebt u geen echte rekenkundige reeks.
4 Vergelijk uw resultaten. De twee resultaten die u krijgt, van optellen vanaf de bodem of van het aftrekken van de bovenkant moeten overeenkomen. Als dat het geval is, hebt u de waarde voor de ontbrekende term gevonden. Als dat niet het geval is, moet u uw werk controleren. Mogelijk hebt u geen echte rekenkundige reeks. 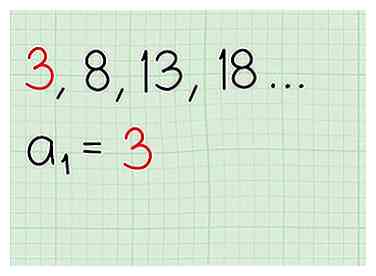 1 Identificeer de eerste termijn van de reeks. Niet elke reeks begint met de cijfers 0 of 1. Bekijk de lijst met nummers die u hebt en zoek de eerste term. Dit is uw startpunt, dat kan worden aangewezen met behulp van variabelen als (1).
1 Identificeer de eerste termijn van de reeks. Niet elke reeks begint met de cijfers 0 of 1. Bekijk de lijst met nummers die u hebt en zoek de eerste term. Dit is uw startpunt, dat kan worden aangewezen met behulp van variabelen als (1). 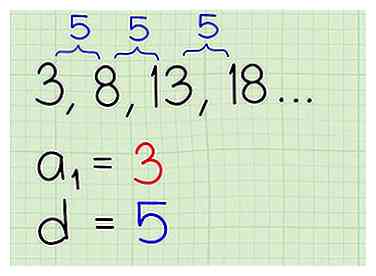 2 Definieer je gemeenschappelijke verschil als d. Zoek het gemeenschappelijke verschil voor de reeks zoals eerder. In dit werkvoorbeeld is het gemeenschappelijke verschil
2 Definieer je gemeenschappelijke verschil als d. Zoek het gemeenschappelijke verschil voor de reeks zoals eerder. In dit werkvoorbeeld is het gemeenschappelijke verschil 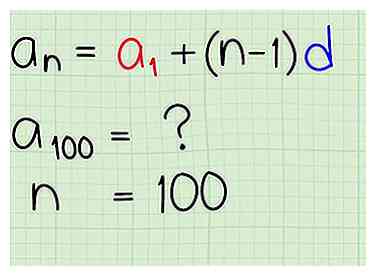 3 Gebruik de expliciete formule. Een expliciete formule is een algebraïsche vergelijking die u kunt gebruiken om een willekeurige rij van een rekenkundige reeks te vinden, zonder dat u de volledige lijst hoeft te schrijven. De expliciete formule voor een algebraïsche sequentie is
3 Gebruik de expliciete formule. Een expliciete formule is een algebraïsche vergelijking die u kunt gebruiken om een willekeurige rij van een rekenkundige reeks te vinden, zonder dat u de volledige lijst hoeft te schrijven. De expliciete formule voor een algebraïsche sequentie is 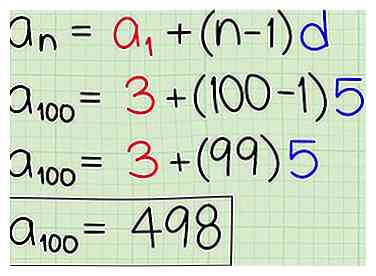 4 Vul uw gegevens in om het probleem op te lossen. Gebruik de expliciete formule voor uw reeks en vul de informatie in die u kent om de term te vinden die u nodig hebt.
4 Vul uw gegevens in om het probleem op te lossen. Gebruik de expliciete formule voor uw reeks en vul de informatie in die u kent om de term te vinden die u nodig hebt. 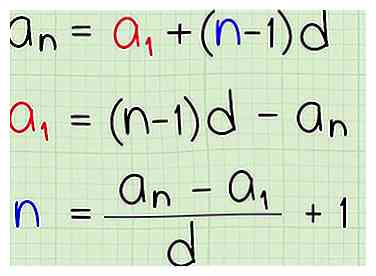 1 Herschik de expliciete formule om op te lossen voor andere variabelen. Met behulp van de expliciete formule en enkele basisalgebra kun je verschillende stukjes informatie over een rekenkundige reeks vinden. In de oorspronkelijke vorm,
1 Herschik de expliciete formule om op te lossen voor andere variabelen. Met behulp van de expliciete formule en enkele basisalgebra kun je verschillende stukjes informatie over een rekenkundige reeks vinden. In de oorspronkelijke vorm, 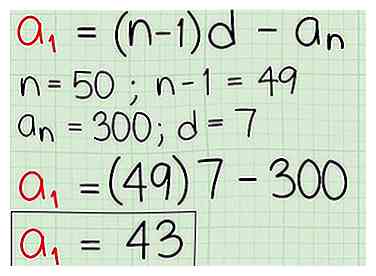 2 Zoek de eerste term van een reeks. Je weet misschien dat de 50e termijn van een rekenkundige reeks 300 is, en je weet dat de termen met 7 zijn toegenomen (het "gemeenschappelijke verschil"), maar je wilt weten wat de eerste term van de reeks was. Gebruik de herziene expliciete formule die lost voor a1 om uw antwoord te vinden.
2 Zoek de eerste term van een reeks. Je weet misschien dat de 50e termijn van een rekenkundige reeks 300 is, en je weet dat de termen met 7 zijn toegenomen (het "gemeenschappelijke verschil"), maar je wilt weten wat de eerste term van de reeks was. Gebruik de herziene expliciete formule die lost voor a1 om uw antwoord te vinden. 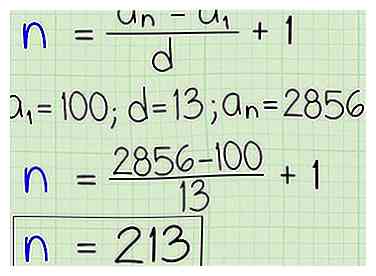 3 Zoek de lengte van een reeks. Stel dat je alles weet over het begin en einde van een rekenkundige reeks, maar je moet weten hoe lang het is. Gebruik de herziene formule
3 Zoek de lengte van een reeks. Stel dat je alles weet over het begin en einde van een rekenkundige reeks, maar je moet weten hoe lang het is. Gebruik de herziene formule