Binomials zijn kleine wiskundige uitdrukkingen die bestaan uit een variabele term (x, a, 3x, 4t, 1090y) opgeteld of afgetrokken met een constante looptijd (1, 3, 110, etc.). Binomials zullen altijd slechts 2 termen bevatten, maar het zijn de bouwstenen van veel grotere en complexere vergelijkingen die bekend staan als polynomen, waardoor ze ongelooflijk belangrijk zijn om goed te leren. Deze les behandelt verschillende soorten binomiale vermenigvuldiging, maar ze kunnen ook allemaal apart worden geleerd.
Methode één van de drie:
Twee binomials vermenigvuldigen
-
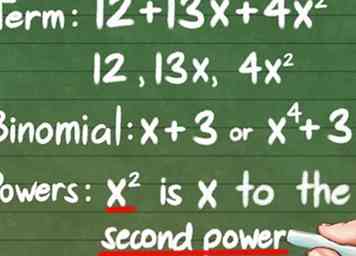 1 Begrijp wiskundig vocabulaire en vraagtypes. Het is onmogelijk om de vragen over uw volgende test op te lossen als u niet weet wat ze vragen. Gelukkig is de terminologie niet ongelooflijk moeilijk:
1 Begrijp wiskundig vocabulaire en vraagtypes. Het is onmogelijk om de vragen over uw volgende test op te lossen als u niet weet wat ze vragen. Gelukkig is de terminologie niet ongelooflijk moeilijk: - Voorwaarden: Een term is gewoon een deel van de vergelijking die wordt toegevoegd of afgetrokken. Het kan een constante, een variabele of beide zijn. Bijvoorbeeld in 12 + 13x + 4x2, de voorwaarden zijn 12, 13x, en 4x2.
- binomiaal: Dit is gewoon een gecompliceerde manier om 'een uitdrukking met twee termen' te zeggen x + 3 of X4 - 3x.
- Powers: dit verwijst naar een exponent voor een term. We zouden bijvoorbeeld kunnen zeggen dat x2 is "x voor de tweede macht."
- Elke vraag die je vraagt om "Zoek de termen van twee binomials (x + 3) (x + 2)," "vind het product van twee binomials," of "expandeer de twee binomials", vraagt je om binomials te vermenigvuldigen.
-
 2 Leer de afkorting FOIL om de volgorde van binominale vermenigvuldiging te onthouden. FOIL is een eenvoudige handleiding voor het vermenigvuldigen van twee binomials. FOIL staat voor de volgorde die u nodig hebt om de delen van de binomials samen te vermenigvuldigen: F is voor Eerste, O is voor Buitenste, Ik ben voor Inner, en L is voor Laatste. De namen verwijzen naar de volgorde waarin de voorwaarden zijn geschreven. Laten we zeggen dat we de binomials (x + 2) en (x + 5) vermenigvuldigen. De voorwaarden zouden zijn:
2 Leer de afkorting FOIL om de volgorde van binominale vermenigvuldiging te onthouden. FOIL is een eenvoudige handleiding voor het vermenigvuldigen van twee binomials. FOIL staat voor de volgorde die u nodig hebt om de delen van de binomials samen te vermenigvuldigen: F is voor Eerste, O is voor Buitenste, Ik ben voor Inner, en L is voor Laatste. De namen verwijzen naar de volgorde waarin de voorwaarden zijn geschreven. Laten we zeggen dat we de binomials (x + 2) en (x + 5) vermenigvuldigen. De voorwaarden zouden zijn: - Eerste: x & x
- Buitenste: x & 5
- Inner: 2 & x
- Laatste: 2 & 5
-
 3 Vermenigvuldig het EERSTE deel tussen haakjes. Dit is de "F" van FOIL. In ons voorbeeld, (x + 2) (x + 5), zijn de eerste termen "x" en "x." Vermenigvuldig deze samen en noteer het antwoord: "x2."
3 Vermenigvuldig het EERSTE deel tussen haakjes. Dit is de "F" van FOIL. In ons voorbeeld, (x + 2) (x + 5), zijn de eerste termen "x" en "x." Vermenigvuldig deze samen en noteer het antwoord: "x2." - Eerste term: x * x = x2
-
 4 Vermenigvuldig de OUTER-onderdelen tussen haakjes. Dit zijn twee buitenste "uiteinden" van ons probleem. Dus in ons voorbeeld (x + 2) (x + 5) zouden ze "x" en "5" zijn. Samen maken ze "5x"
4 Vermenigvuldig de OUTER-onderdelen tussen haakjes. Dit zijn twee buitenste "uiteinden" van ons probleem. Dus in ons voorbeeld (x + 2) (x + 5) zouden ze "x" en "5" zijn. Samen maken ze "5x" - Outer Term: x * 5 = 5x
-
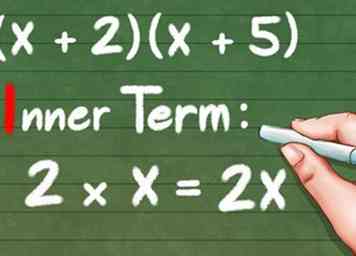 5 Vermenigvuldig de INNERLIJKE delen tussen haakjes. De twee nummers die het dichtst bij het centrum staan, zijn je innerlijke termijn. Voor (x + 2) (x + 5) betekent dit dat u "2" en "x" vermenigvuldigt om "2x" te krijgen.
5 Vermenigvuldig de INNERLIJKE delen tussen haakjes. De twee nummers die het dichtst bij het centrum staan, zijn je innerlijke termijn. Voor (x + 2) (x + 5) betekent dit dat u "2" en "x" vermenigvuldigt om "2x" te krijgen. - Innerlijke Termijn: 2 * x = 2x
-
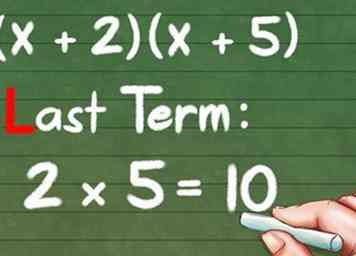 6 Vermenigvuldig de LAATSTE delen tussen haakjes. Dit doet niet de laatste twee getallen, maar eerder het laatste getal tussen haakjes. Dus voor (x + 2) (x + 5) vermenigvuldigen we de "2" en de "5" om "10" te krijgen.
6 Vermenigvuldig de LAATSTE delen tussen haakjes. Dit doet niet de laatste twee getallen, maar eerder het laatste getal tussen haakjes. Dus voor (x + 2) (x + 5) vermenigvuldigen we de "2" en de "5" om "10" te krijgen. - Laatste periode: 2 * 5 = 10
-
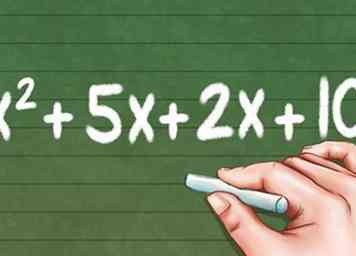 7 Voeg alle nieuwe termen samen toe. Combineer de voorwaarden door ze samen toe te voegen om een nieuwe, grotere expressie te maken. Van ons vorige voorbeeld krijgen we de vergelijking:
7 Voeg alle nieuwe termen samen toe. Combineer de voorwaarden door ze samen toe te voegen om een nieuwe, grotere expressie te maken. Van ons vorige voorbeeld krijgen we de vergelijking: - X2 + 5x + 2x + 10
-
 8 Vereenvoudig soortgelijke termen. Soortgelijke termen zijn delen van de vergelijking met dezelfde variabele en kracht. In ons voorbeeld delen de termen 2x en 5x beide een x en kunnen ze bij elkaar worden opgeteld. Geen andere voorwaarden zijn hetzelfde, dus blijven ze zitten.
8 Vereenvoudig soortgelijke termen. Soortgelijke termen zijn delen van de vergelijking met dezelfde variabele en kracht. In ons voorbeeld delen de termen 2x en 5x beide een x en kunnen ze bij elkaar worden opgeteld. Geen andere voorwaarden zijn hetzelfde, dus blijven ze zitten. - Definitieve antwoord: (x + 2) (x + 5) = X2 + 7x + 10
- Geavanceerde opmerking: Om te leren hoe termen werken, onthoud de basisbeginselen van vermenigvuldiging. 3 * 5 betekent bijvoorbeeld dat je drie vijven bij elkaar optelt om 15 (5 + 5 + 5) te krijgen. In onze vergelijking hebben we 5 * x (x + x + x + x + x) en 2 * x (x + x). Als we alle "x" s in de vergelijking optellen, krijgen we zeven "x" s, of 7x.
-
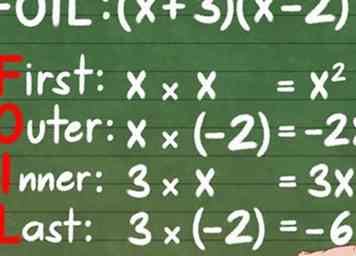 9 Onthoud dat de afgetrokken getallen negatief zijn. Wanneer een getal wordt afgetrokken, is dit hetzelfde als een negatief getal toevoegen. Als u vergeet om het minteken tijdens uw berekeningen te behouden, krijgt u het verkeerde antwoord. Neem het voorbeeld (x + 3) (x-2):
9 Onthoud dat de afgetrokken getallen negatief zijn. Wanneer een getal wordt afgetrokken, is dit hetzelfde als een negatief getal toevoegen. Als u vergeet om het minteken tijdens uw berekeningen te behouden, krijgt u het verkeerde antwoord. Neem het voorbeeld (x + 3) (x-2): - Eerste: x * x = x2
- Buitenste: x * -2 = -2x
- Inner: 3 * x = 3x
- Laatste: 3 * -2 = -6
- Voeg alle termen samen toe: X2 - 2x + 3x - 6
- Vereenvoudig tot definitief antwoord: X2 + x - 6
Methode twee van drie:
Meer dan twee binomials vermenigvuldigen
-
 1 Vermenigvuldig de eerste twee binomials en negeer tijdelijk de derde. Neem het voorbeeld (x + 4) (x + 1) (x + 3). We moeten de binomials één voor één vermenigvuldigen, dus vermenigvuldig de twee door FOIL of door de verdeling van termen. Het vermenigvuldigen van de eerste twee, (x + 4) en (x + 1) met FOIL zou er als volgt uitzien:
1 Vermenigvuldig de eerste twee binomials en negeer tijdelijk de derde. Neem het voorbeeld (x + 4) (x + 1) (x + 3). We moeten de binomials één voor één vermenigvuldigen, dus vermenigvuldig de twee door FOIL of door de verdeling van termen. Het vermenigvuldigen van de eerste twee, (x + 4) en (x + 1) met FOIL zou er als volgt uitzien: - Eerste: x * x = x2
- Buitenste: 1 * x = x
- Inner: 4 * x = 4x
- Laatste: 1*4 = 4
- Combineer voorwaarden: X2 + x + 4x + 4
- (x + 4) (x + 1) = X2 + 5x +4
-
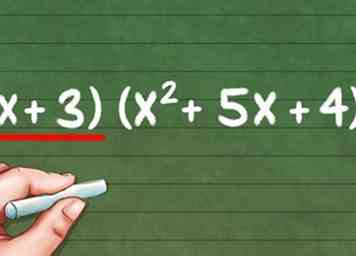 2 Combineer de overgebleven binomiaal met je nieuwe vergelijking. Nu dat deel van de vergelijking vermenigvuldigd is, kun je de overgebleven binomiaal aan. In het voorbeeld (x + 4) (x + 1) (x + 3) was de resterende looptijd (x + 3). Zet het samen met de nieuwe vergelijking terug, en geef het volgende: (X + 3) (x2 + 5x + 4).
2 Combineer de overgebleven binomiaal met je nieuwe vergelijking. Nu dat deel van de vergelijking vermenigvuldigd is, kun je de overgebleven binomiaal aan. In het voorbeeld (x + 4) (x + 1) (x + 3) was de resterende looptijd (x + 3). Zet het samen met de nieuwe vergelijking terug, en geef het volgende: (X + 3) (x2 + 5x + 4). -
 3 Vermenigvuldig het eerste getal in de binomiaal door alle drie de getallen in de andere haakjes. Dit is de verdeling van termen. Dus voor de vergelijking (x + 3) (x2 + 5x + 4), moet u de eerste x vermenigvuldigen met de drie delen van de tweede haakjes, "x2, "" 5x, "en" 4. "
3 Vermenigvuldig het eerste getal in de binomiaal door alle drie de getallen in de andere haakjes. Dit is de verdeling van termen. Dus voor de vergelijking (x + 3) (x2 + 5x + 4), moet u de eerste x vermenigvuldigen met de drie delen van de tweede haakjes, "x2, "" 5x, "en" 4. " - (x * x2) + (x * 5x) + (x * 4) = X3 + 5x2 + 4x
- Schrijf dit antwoord op en bewaar het voor later.
-
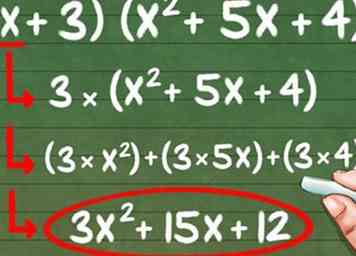 4 Vermenigvuldig het tweede getal in de binomiaal door alle drie de getallen in de andere haakjes. Neem de vergelijking, (x + 3) (x2 + 5x + 4). Verdeel nu het tweede deel van de binomiaal door alle drie de delen in de andere haakjes, "x2, "" 5x, "en" 4. "
4 Vermenigvuldig het tweede getal in de binomiaal door alle drie de getallen in de andere haakjes. Neem de vergelijking, (x + 3) (x2 + 5x + 4). Verdeel nu het tweede deel van de binomiaal door alle drie de delen in de andere haakjes, "x2, "" 5x, "en" 4. " - (3 * x2) + (3 * 5x) + (3 * 4) = 3x2 + 15x + 12
- Schrijf dit antwoord op naast het eerste antwoord.
-
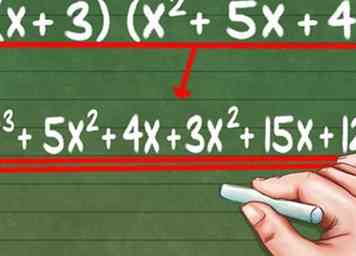 5 Voeg de twee antwoorden samen door vermenigvuldiging. Je moet de antwoorden van de vorige twee stappen combineren, omdat ze de twee delen van je uiteindelijke antwoord vormen.
5 Voeg de twee antwoorden samen door vermenigvuldiging. Je moet de antwoorden van de vorige twee stappen combineren, omdat ze de twee delen van je uiteindelijke antwoord vormen. - X3 + 5x2 + 4x + 3x2 + 15x + 12
-
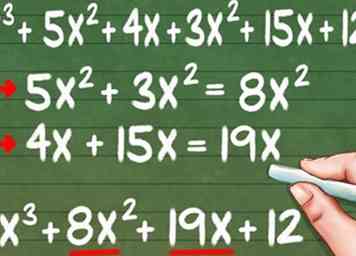 6 Vereenvoudig de vergelijking om uw uiteindelijke antwoord te krijgen. Alle "soortgelijke" voorwaarden, termen die dezelfde variabele en macht delen (zoals 5x2 en 3x2), kunnen bij elkaar worden opgeteld om uw antwoord eenvoudiger te maken.
6 Vereenvoudig de vergelijking om uw uiteindelijke antwoord te krijgen. Alle "soortgelijke" voorwaarden, termen die dezelfde variabele en macht delen (zoals 5x2 en 3x2), kunnen bij elkaar worden opgeteld om uw antwoord eenvoudiger te maken. - 5x2 en 3x2 word 8x2
- 4x en 15x worden 19x
- (x + 4) (x + 1) (x + 3) = X3 + 8x2 + 19x + 12
-
 7 Gebruik altijd distributie om grotere vermenigvuldigingsproblemen aan te pakken. Omdat u de verdeling van termen kunt gebruiken om vergelijkingen van elke lengte te vermenigvuldigen, beschikt u nu over de hulpmiddelen die u nodig hebt om grotere problemen op te lossen, zoals (x + 1) (x + 2) (x + 3). Vermenigvuldig elke willekeurige twee binomialen met behulp van ofwel de verdeling van termen of FOIL, gebruik dan de verdeling van termen om de laatste binomiaal te vermenigvuldigen met de eerste twee. In het volgende voorbeeld gebruiken we FOIL (x + 1) (x + 2) en distribueren we de termen met (x + 3) om het definitieve antwoord te krijgen:
7 Gebruik altijd distributie om grotere vermenigvuldigingsproblemen aan te pakken. Omdat u de verdeling van termen kunt gebruiken om vergelijkingen van elke lengte te vermenigvuldigen, beschikt u nu over de hulpmiddelen die u nodig hebt om grotere problemen op te lossen, zoals (x + 1) (x + 2) (x + 3). Vermenigvuldig elke willekeurige twee binomialen met behulp van ofwel de verdeling van termen of FOIL, gebruik dan de verdeling van termen om de laatste binomiaal te vermenigvuldigen met de eerste twee. In het volgende voorbeeld gebruiken we FOIL (x + 1) (x + 2) en distribueren we de termen met (x + 3) om het definitieve antwoord te krijgen: - (x + 1) (x + 2) (x + 3) = (x + 1) (x + 2) * (x + 3)
- (x + 1) (x + 2) = x2 + 3x + 2
- (x + 1) (x + 2) (x + 3) = (x2 + 3: + 2) * (x + 3)
- (X2 + 3x + 2) * (x + 3) = x3 + 3x2 + 2x + 3x2 + 9x + 6
- Vereenvoudig tot definitief antwoord: X3 + 6x2 + 11x + 6
Methode drie van drie:
Squaring binomials
-
 1 Weet hoe u "algemene formules" moet instellen."Met algemene formules kunt u eenvoudig uw nummers inpluggen in plaats van elke keer FOIL te berekenen. Binomials die worden verhoogd naar de tweede macht, zoals (x + 2)2of de derde macht, zoals (4y + 12)3, kan gemakkelijk in een reeds bestaande formule worden ingebouwd, waardoor het oplossen snel en gemakkelijk gaat. Om de algemene formule te vinden, vervangen we alle getallen door variabelen. Daarna kunnen we aan het einde onze cijfers opnieuw invullen om ons antwoord te krijgen. Begin met de vergelijking (a + b)2, waar:
1 Weet hoe u "algemene formules" moet instellen."Met algemene formules kunt u eenvoudig uw nummers inpluggen in plaats van elke keer FOIL te berekenen. Binomials die worden verhoogd naar de tweede macht, zoals (x + 2)2of de derde macht, zoals (4y + 12)3, kan gemakkelijk in een reeds bestaande formule worden ingebouwd, waardoor het oplossen snel en gemakkelijk gaat. Om de algemene formule te vinden, vervangen we alle getallen door variabelen. Daarna kunnen we aan het einde onze cijfers opnieuw invullen om ons antwoord te krijgen. Begin met de vergelijking (a + b)2, waar: - een staat voor de variabele term (d.w.z. 4y - 1, 2x2 + 3, etc.) Als er geen nummer is, dan is a = 1, omdat 1 * x = x.
- b staat voor het constant worden toegevoegd of afgetrokken (dwz x + 10, t - 12).
-
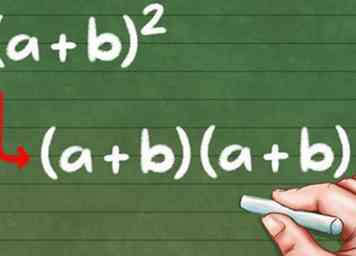 2 Weet dat vierkante binomials herschreven kunnen worden. (a + b)2 lijkt ingewikkelder dan ons eerdere voorbeeld, maar onthoud dat een getal kwadrateren, vermenigvuldigt het alleen. Zodoende kunnen we de vergelijking herschrijven om er meer vertrouwd uit te zien:
2 Weet dat vierkante binomials herschreven kunnen worden. (a + b)2 lijkt ingewikkelder dan ons eerdere voorbeeld, maar onthoud dat een getal kwadrateren, vermenigvuldigt het alleen. Zodoende kunnen we de vergelijking herschrijven om er meer vertrouwd uit te zien: - (a + b)2 = (a + b) (a + b)
-
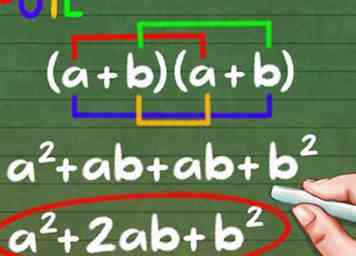 3 Gebruik FOLIE om de nieuwe vergelijking op te lossen. Als we deze vergelijking gebruiken, krijgen we een algemene formule die lijkt op de oplossing voor elke binomiale vermenigvuldiging. Vergeet niet dat in vermenigvuldiging de volgorde waarin u meerdere doet er niet toe doet
3 Gebruik FOLIE om de nieuwe vergelijking op te lossen. Als we deze vergelijking gebruiken, krijgen we een algemene formule die lijkt op de oplossing voor elke binomiale vermenigvuldiging. Vergeet niet dat in vermenigvuldiging de volgorde waarin u meerdere doet er niet toe doet - Herschrijf als (a + b) (a + b).
- Eerste: a * a = a2
- Inner: b * a = ba
- Buitenste: a * b = ab
- Laatste: b * b = b2.
- Voeg de nieuwe voorwaarden toe: een2 + ba + ab + b2
- Combineer dezelfde voorwaarden: een2 + 2ab + b2
- Geavanceerde opmerking: Exponenten en radicalen worden als hyper-3-operaties beschouwd, terwijl vermenigvuldiging en deling hyper-2 zijn. Dit betekent dat eigenschappen van vermenigvuldiging en delen niet werken voor exponenten. (A + b)2 is niet gelijk aan a2 + b2. Dit is een veel voorkomende fout bij mensen.
-
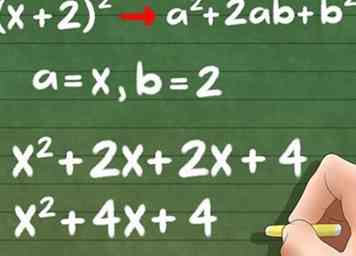 4 Gebruik de algemene vergelijking a2 + 2ab + b2 om uw problemen op te lossen. Laten we een vergelijking maken (x + 2)2. In plaats van FOIL opnieuw te doen, kunnen we de eerste term voor 'a' en de tweede term voor 'b' inpluggen,
4 Gebruik de algemene vergelijking a2 + 2ab + b2 om uw problemen op te lossen. Laten we een vergelijking maken (x + 2)2. In plaats van FOIL opnieuw te doen, kunnen we de eerste term voor 'a' en de tweede term voor 'b' inpluggen, - Algemene vergelijking: a2 + 2ab + b2
- a = x, b = 2
- X2 + (2 * x * 2) + 22
- Definitieve antwoord: X2 + 4x + 4.
- U kunt uw werk altijd controleren door FOIL uit te voeren op de oorspronkelijke vergelijking, (x + 2) (x + 2). Je krijgt elke keer hetzelfde antwoord als je het goed hebt gedaan.
- Als een term wordt afgetrokken, moet je deze nog steeds negatief houden in de algemene vergelijking.
-
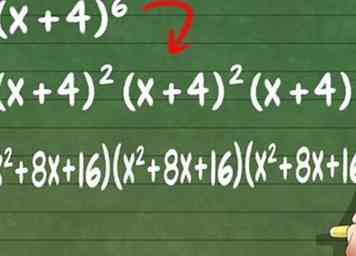 5 Vergeet niet om de hele term in de algemene vergelijking in te voegen. Gezien de binomiale (2x + 3)2, je moet niet vergeten dat a = 2x, niet simpelweg a = 2. Als je complexe termen hebt, moet je onthouden dat zowel de 2 als de x vierkant zijn.
5 Vergeet niet om de hele term in de algemene vergelijking in te voegen. Gezien de binomiale (2x + 3)2, je moet niet vergeten dat a = 2x, niet simpelweg a = 2. Als je complexe termen hebt, moet je onthouden dat zowel de 2 als de x vierkant zijn. - Algemene vergelijking: a2 + 2ab + b2
- Substituut voor a en b: (2x)2 + 2 (2x) (3) + 32
- Vierkant elke term: (22)(X2) + 14x + 32
- Vereenvoudig tot definitief antwoord: 4x2 + 14x + 9
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
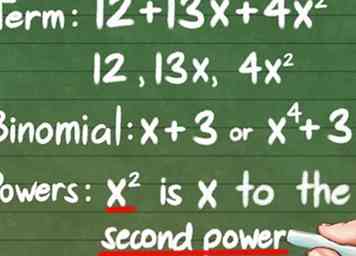 1 Begrijp wiskundig vocabulaire en vraagtypes. Het is onmogelijk om de vragen over uw volgende test op te lossen als u niet weet wat ze vragen. Gelukkig is de terminologie niet ongelooflijk moeilijk:
1 Begrijp wiskundig vocabulaire en vraagtypes. Het is onmogelijk om de vragen over uw volgende test op te lossen als u niet weet wat ze vragen. Gelukkig is de terminologie niet ongelooflijk moeilijk:  2 Leer de afkorting FOIL om de volgorde van binominale vermenigvuldiging te onthouden. FOIL is een eenvoudige handleiding voor het vermenigvuldigen van twee binomials. FOIL staat voor de volgorde die u nodig hebt om de delen van de binomials samen te vermenigvuldigen: F is voor Eerste, O is voor Buitenste, Ik ben voor Inner, en L is voor Laatste. De namen verwijzen naar de volgorde waarin de voorwaarden zijn geschreven. Laten we zeggen dat we de binomials (x + 2) en (x + 5) vermenigvuldigen. De voorwaarden zouden zijn:
2 Leer de afkorting FOIL om de volgorde van binominale vermenigvuldiging te onthouden. FOIL is een eenvoudige handleiding voor het vermenigvuldigen van twee binomials. FOIL staat voor de volgorde die u nodig hebt om de delen van de binomials samen te vermenigvuldigen: F is voor Eerste, O is voor Buitenste, Ik ben voor Inner, en L is voor Laatste. De namen verwijzen naar de volgorde waarin de voorwaarden zijn geschreven. Laten we zeggen dat we de binomials (x + 2) en (x + 5) vermenigvuldigen. De voorwaarden zouden zijn:  3 Vermenigvuldig het EERSTE deel tussen haakjes. Dit is de "F" van FOIL. In ons voorbeeld, (x + 2) (x + 5), zijn de eerste termen "x" en "x." Vermenigvuldig deze samen en noteer het antwoord: "x2."
3 Vermenigvuldig het EERSTE deel tussen haakjes. Dit is de "F" van FOIL. In ons voorbeeld, (x + 2) (x + 5), zijn de eerste termen "x" en "x." Vermenigvuldig deze samen en noteer het antwoord: "x2."  4 Vermenigvuldig de OUTER-onderdelen tussen haakjes. Dit zijn twee buitenste "uiteinden" van ons probleem. Dus in ons voorbeeld (x + 2) (x + 5) zouden ze "x" en "5" zijn. Samen maken ze "5x"
4 Vermenigvuldig de OUTER-onderdelen tussen haakjes. Dit zijn twee buitenste "uiteinden" van ons probleem. Dus in ons voorbeeld (x + 2) (x + 5) zouden ze "x" en "5" zijn. Samen maken ze "5x" 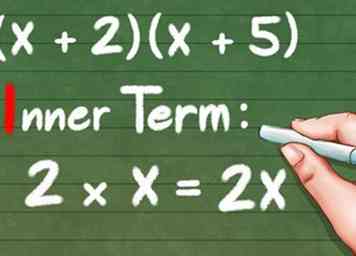 5 Vermenigvuldig de INNERLIJKE delen tussen haakjes. De twee nummers die het dichtst bij het centrum staan, zijn je innerlijke termijn. Voor (x + 2) (x + 5) betekent dit dat u "2" en "x" vermenigvuldigt om "2x" te krijgen.
5 Vermenigvuldig de INNERLIJKE delen tussen haakjes. De twee nummers die het dichtst bij het centrum staan, zijn je innerlijke termijn. Voor (x + 2) (x + 5) betekent dit dat u "2" en "x" vermenigvuldigt om "2x" te krijgen. 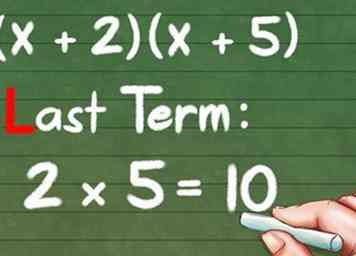 6 Vermenigvuldig de LAATSTE delen tussen haakjes. Dit doet niet de laatste twee getallen, maar eerder het laatste getal tussen haakjes. Dus voor (x + 2) (x + 5) vermenigvuldigen we de "2" en de "5" om "10" te krijgen.
6 Vermenigvuldig de LAATSTE delen tussen haakjes. Dit doet niet de laatste twee getallen, maar eerder het laatste getal tussen haakjes. Dus voor (x + 2) (x + 5) vermenigvuldigen we de "2" en de "5" om "10" te krijgen. 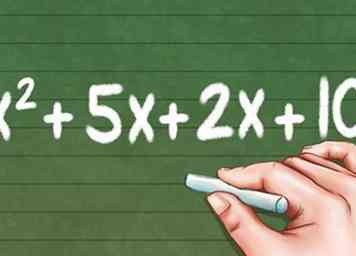 7 Voeg alle nieuwe termen samen toe. Combineer de voorwaarden door ze samen toe te voegen om een nieuwe, grotere expressie te maken. Van ons vorige voorbeeld krijgen we de vergelijking:
7 Voeg alle nieuwe termen samen toe. Combineer de voorwaarden door ze samen toe te voegen om een nieuwe, grotere expressie te maken. Van ons vorige voorbeeld krijgen we de vergelijking:  8 Vereenvoudig soortgelijke termen. Soortgelijke termen zijn delen van de vergelijking met dezelfde variabele en kracht. In ons voorbeeld delen de termen 2x en 5x beide een x en kunnen ze bij elkaar worden opgeteld. Geen andere voorwaarden zijn hetzelfde, dus blijven ze zitten.
8 Vereenvoudig soortgelijke termen. Soortgelijke termen zijn delen van de vergelijking met dezelfde variabele en kracht. In ons voorbeeld delen de termen 2x en 5x beide een x en kunnen ze bij elkaar worden opgeteld. Geen andere voorwaarden zijn hetzelfde, dus blijven ze zitten. 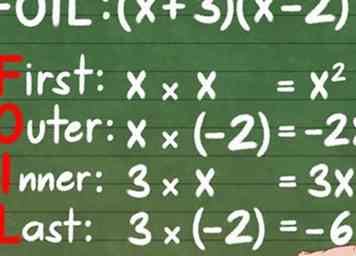 9 Onthoud dat de afgetrokken getallen negatief zijn. Wanneer een getal wordt afgetrokken, is dit hetzelfde als een negatief getal toevoegen. Als u vergeet om het minteken tijdens uw berekeningen te behouden, krijgt u het verkeerde antwoord. Neem het voorbeeld (x + 3) (x-2):
9 Onthoud dat de afgetrokken getallen negatief zijn. Wanneer een getal wordt afgetrokken, is dit hetzelfde als een negatief getal toevoegen. Als u vergeet om het minteken tijdens uw berekeningen te behouden, krijgt u het verkeerde antwoord. Neem het voorbeeld (x + 3) (x-2):  1 Vermenigvuldig de eerste twee binomials en negeer tijdelijk de derde. Neem het voorbeeld (x + 4) (x + 1) (x + 3). We moeten de binomials één voor één vermenigvuldigen, dus vermenigvuldig de twee door FOIL of door de verdeling van termen. Het vermenigvuldigen van de eerste twee, (x + 4) en (x + 1) met FOIL zou er als volgt uitzien:
1 Vermenigvuldig de eerste twee binomials en negeer tijdelijk de derde. Neem het voorbeeld (x + 4) (x + 1) (x + 3). We moeten de binomials één voor één vermenigvuldigen, dus vermenigvuldig de twee door FOIL of door de verdeling van termen. Het vermenigvuldigen van de eerste twee, (x + 4) en (x + 1) met FOIL zou er als volgt uitzien: 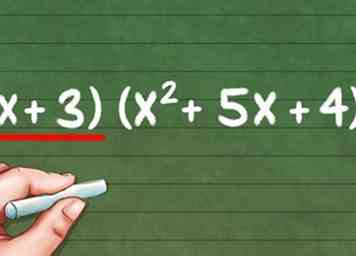 2 Combineer de overgebleven binomiaal met je nieuwe vergelijking. Nu dat deel van de vergelijking vermenigvuldigd is, kun je de overgebleven binomiaal aan. In het voorbeeld (x + 4) (x + 1) (x + 3) was de resterende looptijd (x + 3). Zet het samen met de nieuwe vergelijking terug, en geef het volgende: (X + 3) (x2 + 5x + 4).
2 Combineer de overgebleven binomiaal met je nieuwe vergelijking. Nu dat deel van de vergelijking vermenigvuldigd is, kun je de overgebleven binomiaal aan. In het voorbeeld (x + 4) (x + 1) (x + 3) was de resterende looptijd (x + 3). Zet het samen met de nieuwe vergelijking terug, en geef het volgende: (X + 3) (x2 + 5x + 4).  3 Vermenigvuldig het eerste getal in de binomiaal door alle drie de getallen in de andere haakjes. Dit is de verdeling van termen. Dus voor de vergelijking (x + 3) (x2 + 5x + 4), moet u de eerste x vermenigvuldigen met de drie delen van de tweede haakjes, "x2, "" 5x, "en" 4. "
3 Vermenigvuldig het eerste getal in de binomiaal door alle drie de getallen in de andere haakjes. Dit is de verdeling van termen. Dus voor de vergelijking (x + 3) (x2 + 5x + 4), moet u de eerste x vermenigvuldigen met de drie delen van de tweede haakjes, "x2, "" 5x, "en" 4. " 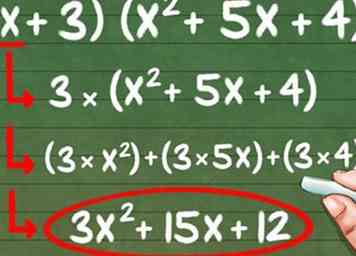 4 Vermenigvuldig het tweede getal in de binomiaal door alle drie de getallen in de andere haakjes. Neem de vergelijking, (x + 3) (x2 + 5x + 4). Verdeel nu het tweede deel van de binomiaal door alle drie de delen in de andere haakjes, "x2, "" 5x, "en" 4. "
4 Vermenigvuldig het tweede getal in de binomiaal door alle drie de getallen in de andere haakjes. Neem de vergelijking, (x + 3) (x2 + 5x + 4). Verdeel nu het tweede deel van de binomiaal door alle drie de delen in de andere haakjes, "x2, "" 5x, "en" 4. " 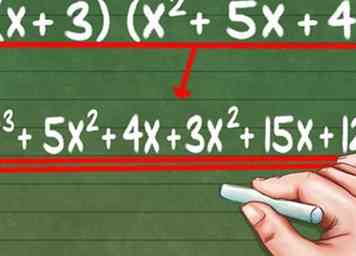 5 Voeg de twee antwoorden samen door vermenigvuldiging. Je moet de antwoorden van de vorige twee stappen combineren, omdat ze de twee delen van je uiteindelijke antwoord vormen.
5 Voeg de twee antwoorden samen door vermenigvuldiging. Je moet de antwoorden van de vorige twee stappen combineren, omdat ze de twee delen van je uiteindelijke antwoord vormen. 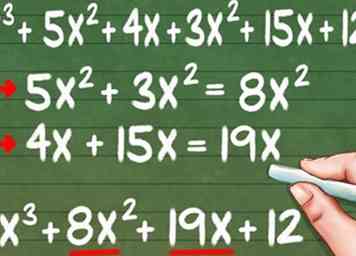 6 Vereenvoudig de vergelijking om uw uiteindelijke antwoord te krijgen. Alle "soortgelijke" voorwaarden, termen die dezelfde variabele en macht delen (zoals 5x2 en 3x2), kunnen bij elkaar worden opgeteld om uw antwoord eenvoudiger te maken.
6 Vereenvoudig de vergelijking om uw uiteindelijke antwoord te krijgen. Alle "soortgelijke" voorwaarden, termen die dezelfde variabele en macht delen (zoals 5x2 en 3x2), kunnen bij elkaar worden opgeteld om uw antwoord eenvoudiger te maken.  7 Gebruik altijd distributie om grotere vermenigvuldigingsproblemen aan te pakken. Omdat u de verdeling van termen kunt gebruiken om vergelijkingen van elke lengte te vermenigvuldigen, beschikt u nu over de hulpmiddelen die u nodig hebt om grotere problemen op te lossen, zoals (x + 1) (x + 2) (x + 3). Vermenigvuldig elke willekeurige twee binomialen met behulp van ofwel de verdeling van termen of FOIL, gebruik dan de verdeling van termen om de laatste binomiaal te vermenigvuldigen met de eerste twee. In het volgende voorbeeld gebruiken we FOIL (x + 1) (x + 2) en distribueren we de termen met (x + 3) om het definitieve antwoord te krijgen:
7 Gebruik altijd distributie om grotere vermenigvuldigingsproblemen aan te pakken. Omdat u de verdeling van termen kunt gebruiken om vergelijkingen van elke lengte te vermenigvuldigen, beschikt u nu over de hulpmiddelen die u nodig hebt om grotere problemen op te lossen, zoals (x + 1) (x + 2) (x + 3). Vermenigvuldig elke willekeurige twee binomialen met behulp van ofwel de verdeling van termen of FOIL, gebruik dan de verdeling van termen om de laatste binomiaal te vermenigvuldigen met de eerste twee. In het volgende voorbeeld gebruiken we FOIL (x + 1) (x + 2) en distribueren we de termen met (x + 3) om het definitieve antwoord te krijgen:  1 Weet hoe u "algemene formules" moet instellen."Met algemene formules kunt u eenvoudig uw nummers inpluggen in plaats van elke keer FOIL te berekenen. Binomials die worden verhoogd naar de tweede macht, zoals (x + 2)2of de derde macht, zoals (4y + 12)3, kan gemakkelijk in een reeds bestaande formule worden ingebouwd, waardoor het oplossen snel en gemakkelijk gaat. Om de algemene formule te vinden, vervangen we alle getallen door variabelen. Daarna kunnen we aan het einde onze cijfers opnieuw invullen om ons antwoord te krijgen. Begin met de vergelijking (a + b)2, waar:
1 Weet hoe u "algemene formules" moet instellen."Met algemene formules kunt u eenvoudig uw nummers inpluggen in plaats van elke keer FOIL te berekenen. Binomials die worden verhoogd naar de tweede macht, zoals (x + 2)2of de derde macht, zoals (4y + 12)3, kan gemakkelijk in een reeds bestaande formule worden ingebouwd, waardoor het oplossen snel en gemakkelijk gaat. Om de algemene formule te vinden, vervangen we alle getallen door variabelen. Daarna kunnen we aan het einde onze cijfers opnieuw invullen om ons antwoord te krijgen. Begin met de vergelijking (a + b)2, waar: 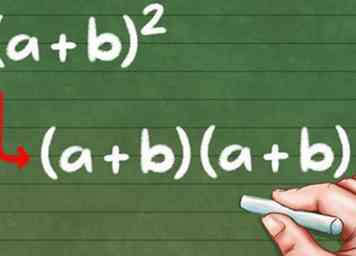 2 Weet dat vierkante binomials herschreven kunnen worden. (a + b)2 lijkt ingewikkelder dan ons eerdere voorbeeld, maar onthoud dat een getal kwadrateren, vermenigvuldigt het alleen. Zodoende kunnen we de vergelijking herschrijven om er meer vertrouwd uit te zien:
2 Weet dat vierkante binomials herschreven kunnen worden. (a + b)2 lijkt ingewikkelder dan ons eerdere voorbeeld, maar onthoud dat een getal kwadrateren, vermenigvuldigt het alleen. Zodoende kunnen we de vergelijking herschrijven om er meer vertrouwd uit te zien: 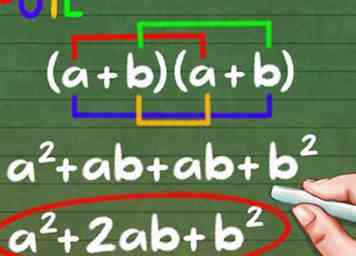 3 Gebruik FOLIE om de nieuwe vergelijking op te lossen. Als we deze vergelijking gebruiken, krijgen we een algemene formule die lijkt op de oplossing voor elke binomiale vermenigvuldiging. Vergeet niet dat in vermenigvuldiging de volgorde waarin u meerdere doet er niet toe doet
3 Gebruik FOLIE om de nieuwe vergelijking op te lossen. Als we deze vergelijking gebruiken, krijgen we een algemene formule die lijkt op de oplossing voor elke binomiale vermenigvuldiging. Vergeet niet dat in vermenigvuldiging de volgorde waarin u meerdere doet er niet toe doet 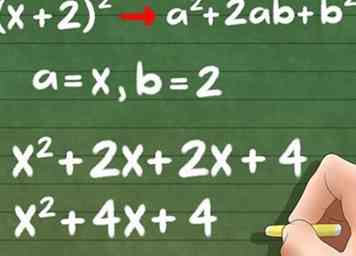 4 Gebruik de algemene vergelijking a2 + 2ab + b2 om uw problemen op te lossen. Laten we een vergelijking maken (x + 2)2. In plaats van FOIL opnieuw te doen, kunnen we de eerste term voor 'a' en de tweede term voor 'b' inpluggen,
4 Gebruik de algemene vergelijking a2 + 2ab + b2 om uw problemen op te lossen. Laten we een vergelijking maken (x + 2)2. In plaats van FOIL opnieuw te doen, kunnen we de eerste term voor 'a' en de tweede term voor 'b' inpluggen, 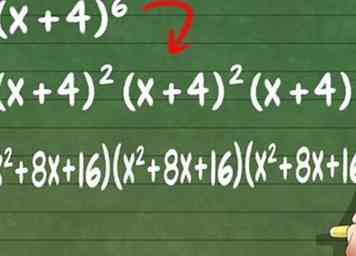 5 Vergeet niet om de hele term in de algemene vergelijking in te voegen. Gezien de binomiale (2x + 3)2, je moet niet vergeten dat a = 2x, niet simpelweg a = 2. Als je complexe termen hebt, moet je onthouden dat zowel de 2 als de x vierkant zijn.
5 Vergeet niet om de hele term in de algemene vergelijking in te voegen. Gezien de binomiale (2x + 3)2, je moet niet vergeten dat a = 2x, niet simpelweg a = 2. Als je complexe termen hebt, moet je onthouden dat zowel de 2 als de x vierkant zijn.