Hoe ongelijkheid te berekenen

U kunt een lineaire of kwadratische ongelijkheid plotten op dezelfde manier als waarop u een vergelijking zou tekenen. Het verschil is dat, aangezien een ongelijkheid een reeks waarden groter of kleiner dan, toont, uw grafiek meer dan alleen een punt op een getallenlijn of een lijn op een coördinaatvlak zal tonen. Door algebra te gebruiken en het ongelijkheidsteken te evalueren, kunt u bepalen welke waarden zijn opgenomen in de oplossing van een ongelijkheid.

Methode één van de drie:
Een lineaire ongelijkheid grafisch weergeven op een getallenlijn

1. 1 Los op voor de variabele. Om de ongelijkheid op te lossen, isoleert u de variabele met dezelfde algebraïsche methoden die u zou gebruiken om een ​​vergelijking op te lossen.^[1] Onthoud dat wanneer u zich vermenigvuldigt of deelt door een negatief getal, u het ongelijkheidsteken moet omdraaien.
   • Bijvoorbeeld als u de ongelijkheid oplost $\ displaystyle 3y + 9> 12$, isoleer de variabele door 9 van elke kant van de ongelijkheid af te trekken en deel dan door 3:
     $\ displaystyle 3y + 9> 12$
     $\ displaystyle 3y + 9-9> 12-9$
     $\ displaystyle 3y> 3$
     $\ displaystyle \ frac 3y 3> \ frac 3 3$
     $\ displaystyle y> 1$
   • Uw ongelijkheid zou slechts één variabele moeten hebben. Als uw ongelijkheid twee variabelen heeft, is het passender om het op een coördinatenvlak te tekenen met een andere methode.
2. 2 Teken een getallenlijn. Neem de relatieve waarde op uw getallenlijn op (de waarde waarvan u vond dat de variabele kleiner dan, groter dan of gelijk aan was). Maak de nummerregel zo lang of kort als nodig is.
   • Bijvoorbeeld, als je dat hebt gevonden $\ displaystyle y> 1$, zorg ervoor dat u een punt voor 1 op de getallenlijn plaatst.
3. 3 Teken een cirkel die de relatieve waarde aangeeft. Als de waarde kleiner is dan ($\ displaystyle <$) of groter dan ($\ displaystyle>$) dit aantal moet de cirkel open zijn, omdat de oplossing de waarde niet bevat. Als de waarde kleiner is dan of gelijk aan ($\ displaystyle \ leq$), of groter dan of gelijk aan ($\ displaystyle \ geq$), moet de cirkel worden ingevuld, omdat de oplossing de waarde bevat.^[2]
   • Bijvoorbeeld, als $\ displaystyle y> 1$, zou je een cirkel tekenen op 1 op de getallenlijn. Je zou de cirkel niet invullen, omdat 1 niet in de oplossing is opgenomen.
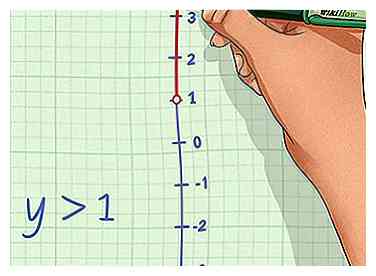4. 4 Teken een pijl die de opgenomen waarden aangeeft. Als de variabele groter is dan de relatieve waarde, moet uw pijl naar rechts wijzen, omdat de oplossing waarden bevat die groter zijn dan dat getal. Als de variabele kleiner is dan de relatieve waarde, moet uw pijl naar links wijzen, omdat de oplossing minder dan dat getal bevat.^[3]
   • Bijvoorbeeld voor de oplossing $\ displaystyle y> 1$, tekent u een pijl naar rechts, omdat de oplossing waarden groter dan 1 bevat.

Methode twee van drie:
Een lineaire ongelijkheid grafisch weergeven op een gecoördineerd vlak

1. 1 Oplossen voor $\ displaystyle y$. Je wilt de vergelijking van de regel vinden, dus daarvoor moet je de. Isoleren $\ displaystyle y$ variabele aan de linkerkant van de vergelijking met behulp van algebra.^[4] De rechterkant van de vergelijking moet de $\ displaystyle x$ variabele en waarschijnlijk een constante.
   • Bijvoorbeeld voor de ongelijkheid $\ displaystyle 3y + 9> 9x$, u isoleert de variabele y door 9 van beide kanten af ​​te trekken en vervolgens te delen door 3:
     $\ displaystyle 3y + 9> 9x$
     $\ displaystyle 3y + 9-9> 9x-9$
     $\ displaystyle 3y> 9x-9$
     $\ displaystyle \ frac 3y 3> \ frac 9x-9 3$
     $\ displaystyle y> 3x-3$
2. 2 Grafiek de lijn op een coördinaatvlak. Om dit te doen, verander de ongelijkheid in een vergelijking, en grafiek zoals elke vergelijking van een lijn.^[5] Teken het y-snijpunt uit en gebruik vervolgens de helling om andere punten op de lijn te tekenen.
   • Bijvoorbeeld als de ongelijkheid is $\ displaystyle y> 3x-3$, zou u de lijn in een grafiek weergeven $\ displaystyle y = 3x-3$. Het y-snijpunt (het punt waar de lijn de y-as passeert) is -3 en de helling is 3, of $\ displaystyle \ frac 3 1$. Dus, je zou een punt trekken naar $\ displaystyle (0, -3)$. Het punt boven het y-snijpunt is $\ displaystyle (1,0)$. Het punt onder het y-snijpunt is $\ displaystyle (-1, -6)$.
3. 3 Trek de grens. Als de ongelijkheid minder is dan ($\ displaystyle <$) of groter dan ($\ displaystyle>$), moet de regel worden gestippeld, omdat de oplossing geen waarden bevat die gelijk zijn aan de regel. Als de waarde kleiner is dan of gelijk aan ($\ displaystyle \ leq$), of groter dan of gelijk aan ($\ displaystyle \ geq$), moet de lijn stabiel zijn, omdat de oplossing waarden bevat die gelijk zijn aan de regel.^[6]
   • Bijvoorbeeld, omdat de ongelijkheid is $\ displaystyle y> 3x-3$, de regel moet worden gestippeld, omdat de waarden geen punten op de regel bevatten.
4. 4 Schaduw in het juiste gebied. Als de ongelijkheid zichtbaar is $\ displaystyle y> mx + b$ je zou moeten overschaduwen in het gebied boven de lijn. Als de ongelijkheid zichtbaar is $\ displaystyle y<>$, u moet het gebied onder de lijn verduisteren.^[7]
   • Bijvoorbeeld voor de ongelijkheid $\ displaystyle y> 3x-3$ je zou boven de lijn overschaduwen.

Methode drie van drie:
Grafische weergave van een kwadratische ongelijkheid op een gecoördineerd vlak

1. 1 Bepaal of je een kwadratische ongelijkheid hebt. Een kwadratische ongelijkheid neemt de vorm aan van $\ displaystyle ax ^ 2 + bx + c$.^[8] Soms is er misschien geen $\ displaystyle x$ term of een constante, maar er moet altijd een zijn $\ displaystyle x ^ 2$ termijn aan de ene kant van de ongelijkheid, en een geïsoleerde $\ displaystyle y$ variabele aan de andere kant.
   • U moet bijvoorbeeld mogelijk de ongelijkheid in kaart brengen $\ displaystyle y<>$.
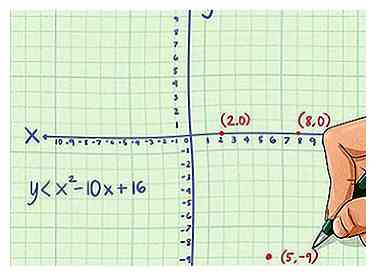2. 2 Grafiek de lijn op een coördinaatvlak. Om dit te doen, verandert u de ongelijkheid in een vergelijking en tekent u de lijn zoals u normaal zou doen. Omdat je een kwadratische vergelijking hebt, is de lijn een parabool.^[9]
   • Bijvoorbeeld voor de ongelijkheid $\ displaystyle y<>$, zou u de lijn in een grafiek weergeven $\ displaystyle y = x ^ 2 -10x + 16$. De vertex is op het punt $\ displaystyle (5, -9)$en de parabool kruist de x-as op de punten $\ displaystyle (2,0)$ en $\ displaystyle (8,0)$.
3. 3 Teken de parabool. Teken de parabool met een streepjeslijn als de ongelijkheid kleiner is dan ($\ displaystyle <$) of groter dan ($\ displaystyle>$). Als de waarde kleiner is dan of gelijk aan ($\ displaystyle \ leq$), of groter dan of gelijk aan ($\ displaystyle \ geq$), moet u de parabool tekenen met een ononderbroken lijn, omdat de oplossing waarden bevat die gelijk zijn aan de lijn.
   • Bijvoorbeeld voor de ongelijkheid $\ displaystyle y<>$, zou je de parabool met een streepjeslijn tekenen.
4. 4 Zoek enkele testpunten. Om te bepalen welk gebied je wilt overschaduwen, moet je punten kiezen in de parabool en buiten de parabool.
   • Bijvoorbeeld de grafiek van de ongelijkheid $\ displaystyle y<>$ laat dat zien $\ displaystyle (0,0)$ is buiten de parabool. Dit zou een goed punt zijn om te gebruiken om de oplossing te testen.
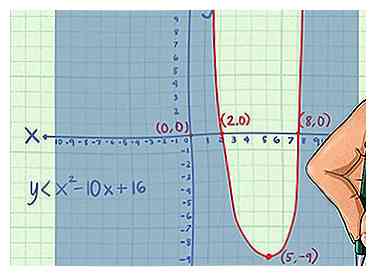5. 5 Schaduw het juiste gebied. Om te bepalen welk schaduwgebied, sluit u de waarden van $\ displaystyle x$ en $\ displaystyle y$ van je testpunten naar de oorspronkelijke ongelijkheid. Welk punt ook een echte ongelijkheid oplevert, geeft aan in welk gebied van de grafiek schaduw moet worden weergegeven.^[10]
   • Sluit bijvoorbeeld de waarden van in $\ displaystyle x$ en $\ displaystyle y$ van het punt $\ displaystyle (0,0)$ in de originele ongelijkheid, krijg je:
     $\ displaystyle y<>$
     $\ displaystyle 0 <0 ^ 2 -0x + 16$
     $\ displaystyle 0 <16$
     Aangezien dit waar is, zou je het gebied van de grafiek waar het punt is verduisteren $\ displaystyle (0,0)$ is gevonden. In dit geval bevindt dit zich buiten de parabool, niet daarbinnen.