3 manieren om een functie te tekenen | Antwoorden op al uw "Hoe?"

Een grafiek van een functie is een visuele weergave van het gedrag van een functie op een x-y-vlak. Grafieken helpen ons verschillende aspecten van de functie te begrijpen, die moeilijk te begrijpen zijn door gewoon naar de functie zelf te kijken. U kunt duizenden vergelijkingen maken en er zijn verschillende formules voor elke vergelijking. Dat gezegd hebbende, er zijn altijd manieren om een functie in een grafiek weer te geven als u de exacte stappen voor het specifieke type functie bent vergeten.

Methode één van de drie:
Grafische lineaire vergelijkingen met helling

1 Herken lineaire functies als eenvoudige, gemakkelijk getekende lijnen, zoals $\ displaystyle y = 2x + 5$ . Er is één variabele en één constante, geschreven als $\ displaystyle F (x) ory = a + bx$ in een lineaire functie, zonder exponenten, radicalen, enz. Als je een eenvoudige vergelijking als deze hebt, dan is het eenvoudig om de functie grafisch weer te geven. Andere voorbeelden van lineaire functies zijn onder meer:
- $\ displaystyle F (n) = 4-2n$
- $\ displaystyle y = 3t-120$
- $\ displaystyle F (x) = \ frac 2 3 x + 3$ ^[1]
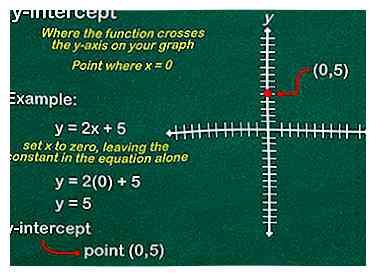2 Gebruik de constante om uw y-snijpunt te markeren. Het y-snijpunt is waar de functie de y-as in uw grafiek doorkruist. Met andere woorden, het is het punt waar $\ displaystyle x = 0$ . Dus om het te vinden, stelt u eenvoudig x in op nul, waarbij u de constante in de vergelijking alleen laat. Voor het eerdere voorbeeld, $\ displaystyle y = 2x + 5$ , uw y-snijpunt is 5, of het punt (0,5). Markeer deze plek in uw grafiek met een punt.
3 Zoek de helling van uw lijn met het getal vlak voor de variabele. In jouw voorbeeld $\ displaystyle y = 2x + 5$ , de helling is "2." Dat komt omdat 2 vlak voor de variabele in de vergelijking staat, de "x". Helling is hoe steil een lijn is, of hoe hoog de lijn is voordat hij naar rechts of links gaat. Grotere hellingen betekenen steilere lijnen.
4 Breek de helling in een fractie. Helling gaat over steilheid en steilheid is gewoon het verschil tussen beweging op en neer en beweging naar links en rechts. Helling is een fractie van rijzen over rennen. Hoeveel stijgt de lijn (ga omhoog) voordat deze "loopt" (gaat naar de zijkant)? Voor het voorbeeld kan de helling van "2" worden gelezen als $\ displaystyle \ frac 2up 1over$ .
- Als de helling negatief is, betekent dit dat de lijn naar beneden gaat als je naar rechts beweegt.
5 Beginnend met je y-snijpunt, volg je "stijgen" en "rennen" om meer punten te berekenen. Als je eenmaal je helling kent, gebruik die dan om je lineaire functie uit te zetten. Begin bij je y-snijpunt, hier (0,5), en ga dan met 2 omhoog, over 1. Markeer ook dit punt (1,7). Zoek nog eens 1-2 punten om een overzicht van je lijn te maken.
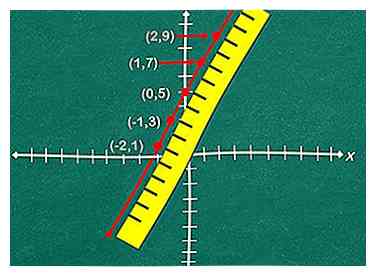6 Gebruik een liniaal om uw punten te verbinden en uw lineaire functie in een grafiek weer te geven. Om fouten of ruwe grafieken te voorkomen, zoekt en verbindt u ten minste drie afzonderlijke punten, hoewel twee in een mum van tijd zullen doen. Dit is de grafiek van uw lineaire vergelijking!

Methode twee van drie:
Punten in een grafiek schatten

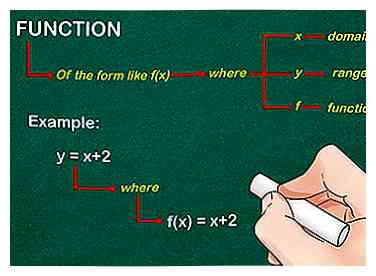1 Bepaal de functie. Krijg de functie van de vorm zoals f(X), waar Y zou het bereik vertegenwoordigen, X zou het domein vertegenwoordigen, en f zou de functie representeren. Als voorbeeld gebruiken we Y = x + 2, waar f(X) = x + 2.
2 Teken twee lijnen in een + vorm op een vel papier. De horizontale lijn is jouw X as. De verticale lijn is jouw Y as.
3 Nummer uw grafiek. Markeer beide X as en de Y as met gelijk gespreide nummers. Voor de X as, de getallen zijn positief aan de rechterkant en negatief aan de linkerkant. Voor de Y as, de getallen zijn positief aan de bovenkant en negatief aan de onderkant.
4 Bereken een Y waarde voor 2-3 X waarden. Neem je functie f(X) = x + 2. Bereken een paar waarden voor Y door de bijbehorende waarden voor te zetten X zichtbaar op de as in de functie. Voor meer gecompliceerde vergelijkingen, wilt u misschien de functie vereenvoudigen door eerst een variabele te isoleren.
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
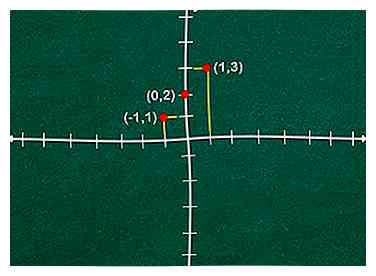5 Teken het grafiekpunt voor elk paar. Schets gewoon denkbeeldige lijnen verticaal voor elk X aswaarde en horizontaal voor elk Y aswaarde. Het punt waar deze lijnen elkaar kruisen is een grafiekpunt.
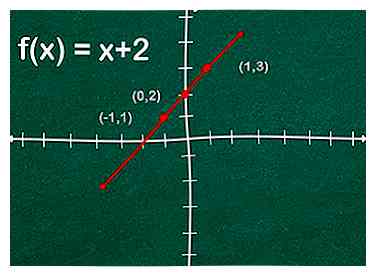6 Verwijder de denkbeeldige lijnen. Nadat u alle grafiekpunten hebt getekend, kunt u de denkbeeldige lijnen wissen. Opmerking: de grafiek van f (x) = x is een lijn evenwijdig aan deze die door de oorsprong (0,0) gaat, maar f (x) = x + 2 wordt twee eenheden naar boven verschoven (langs de y-as) op het rooster vanwege de +2 in de vergelijking.^[2]

Methode drie van drie:
Grafische weergave van gecompliceerde functies met de hand

1 Begrijp hoe u veelgebruikte vergelijkingstypen kunt plotten. Er zijn zoveel verschillende grafische strategieën als er soorten functies zijn, veel te veel om hier volledig te beschrijven. Als je problemen hebt en schattingen niet werken, bekijk dan artikelen over:
- Kwadratische functies
- Rationele functies
- Logaritmische functies
- Grafische ongelijkheden (geen functies, maar nog steeds bruikbare informatie).
2 Zoek eerst nullen. Nullen, ook wel x-onderschept genoemd, zijn de punten waar de grafiek de horizontale lijn in de grafiek overschrijdt. Hoewel niet alle grafieken zelfs nullen hebben, doen de meeste dat wel, en het is de eerste stap die u moet nemen om alles op het goede spoor te krijgen. Om nullen te vinden, simpelweg de hele functie op nul zetten en oplossen. Bijvoorbeeld:
- $\ displaystyle F (x) = 2x ^ 2 -18$
- Stel F (x) gelijk aan nul: $\ displaystyle 0 = 2x ^ 2 -18$
- Oplossen: $\ displaystyle 0 = 2x ^ 2 -18$
  - $\ displaystyle 18 = 2x ^ 2$
  - $\ displaystyle 9 = x ^ 2$
  - $\ displaystyle x = 3, -3$ ^[3]
3 Zoek en markeer horizontale asymptoten of plaatsen waar het onmogelijk is om de functie te gebruiken, met een stippellijn. Dit zijn meestal punten waar de grafiek niet bestaat, zoals waar je door nul deelt. Als je vergelijking een variabele in een breuk heeft, zoals $\ displaystyle y = \ frac 1 4-x ^ 2$ , begin met het instellen van de onderkant van de breuk op nul. Alle plaatsen waar deze gelijk is aan nul kunnen worden gestippeld (in dit voorbeeld een stippellijn op x = 2 en x = -2), omdat je nooit kunt delen door nul. Breuken zijn echter niet de enige plaatsen waar je asymptoten kunt vinden. Meestal is alles wat je nodig hebt wat gezond verstand:
- Sommige vierkante functies, zoals $\ displaystyle F (n) = n ^ 2$ kan nooit negatief zijn. Dus is er een asymptoot op 0.
- Tenzij je met denkbeeldige getallen werkt, kun je dat niet hebben $\ displaystyle \ sqrt -1$ ^[4]
- Voor vergelijkingen met complexe exponenten heb je misschien veel asymptoten.
4 Plug en grafiek meerdere punten in. Kies eenvoudig een paar waarden voor x en los de functie op. Grafiek vervolgens de punten op uw grafiek. Hoe ingewikkelder de grafiek, hoe meer punten je nodig hebt. Over het algemeen zijn -1, 0 en 1 de gemakkelijkste punten om te krijgen, hoewel je aan elke kant van nul nog 2-3 extra wilt om een goede grafiek te krijgen.^[5]
- Voor de vergelijking $\ displaystyle y = 5x ^ 2 +6$ , je zou kunnen plug-in -1,0,1, -2, 2, -10 en 10. Dit geeft je een leuk bereik van te vergelijken aantallen.
- Wees slim door getallen te selecteren. In het voorbeeld zul je snel merken dat het hebben van een negatief teken niet uitmaakt - je kunt bijvoorbeeld stoppen met testen -10, omdat het hetzelfde is als 10.
5 Breng het eindgedrag van de functie in kaart om te zien wat er gebeurt als het echt enorm is. Dit geeft u een idee van de algemene richting van een functie, meestal als een verticaal asymptoot. Bijvoorbeeld - je weet dat dat uiteindelijk $\ displaystyle y = x ^ 2$ wordt echt heel groot. Slechts één extra "x" (één miljoen versus één miljoen en één) maakt y veel groter. Er zijn een paar manieren om eindgedrag te testen, waaronder:
- Sluit 2-4 grote waarden van x, half negatief en half positief in en plot de punten.
- Wat gebeurt er als je voor één variabele "oneindig" hebt aangesloten? Wordt de functie oneindig groter of kleiner?
- Als de graden in een breuk hetzelfde zijn, zoals $\ displaystyle F (x) = \ frac x ^ 3 - 2x ^ 3 +4$ , deel eenvoudig de eerste twee coëfficiënten ( $\ displaystyle \ frac 1 - 2$ om uw beëindigende asymptoot te krijgen (-5).^[6]
- Als de graden in een fractie verschillen, moet u de vergelijking in de teller opsplitsen door de vergelijking in noemer van Polynomial Long Division.
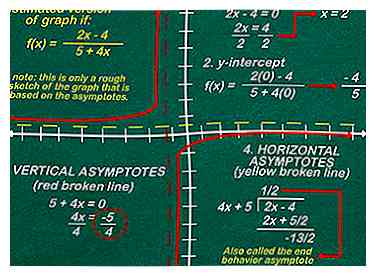6 Verbind de stippen, vermijd asymptotisch en volg het eindgedrag om een schatting van de functie in te stellen. Zodra u 5-6 punten, asymptoten en een algemeen idee van eindgedrag heeft, sluit u deze allemaal aan om een geschatte versie van de grafiek te krijgen.
7 Krijg perfecte grafieken met behulp van een grafische rekenmachine. Grafische rekenmachines zijn krachtige zakcomputers die exacte grafieken voor elke vergelijking kunnen geven. Hiermee kunt u exacte punten zoeken, hellingslijnen vinden en moeizame vergelijkingen gemakkelijk visualiseren. Voer gewoon de exacte vergelijking in het grafische gedeelte in (meestal een knop met het label "F (x) =") en klik op de grafiek om uw functie op het werk te zien.