In de algebra hebben tweedimensionale coördinaatgrafieken een horizontale as, of x-as, en een verticale as, of y-as. De plaatsen waar lijnen die een bereik van waarden vertegenwoordigen door deze assen lopen, worden onderschept genoemd. Het y-snijpunt is de plaats waar de lijn de y-as en het x-snijpunt kruist waar de lijn de x-as kruist. Voor eenvoudige problemen is het gemakkelijk om het X-snijpunt te vinden door naar een grafiek te kijken. U kunt het exacte punt van het snijpunt vinden door algebraïsch op te lossen met behulp van de vergelijking van de lijn.
Methode één van de drie:
Een grafiek van een lijn gebruiken
-
 1 Identificeer de x-as. Een coördinaatgrafiek heeft een y-as en een x-as. De x-as is de horizontale lijn (de lijn die van links naar rechts loopt). De y-as is de verticale lijn (de lijn die omhoog en omlaag gaat).[1] Het is belangrijk om te kijken naar de x-as bij het lokaliseren van het x-snijpunt.
1 Identificeer de x-as. Een coördinaatgrafiek heeft een y-as en een x-as. De x-as is de horizontale lijn (de lijn die van links naar rechts loopt). De y-as is de verticale lijn (de lijn die omhoog en omlaag gaat).[1] Het is belangrijk om te kijken naar de x-as bij het lokaliseren van het x-snijpunt. -
 2 Zoek het punt waar de lijn de x-as kruist. Het X-snijpunt is dit punt.[2] Als u wordt gevraagd om het x-snijpunt op basis van de grafiek te vinden, is het punt waarschijnlijk exact (bijvoorbeeld op punt 4). Meestal moet u echter een schatting maken van deze methode (het punt bevindt zich bijvoorbeeld tussen 4 en 5).
2 Zoek het punt waar de lijn de x-as kruist. Het X-snijpunt is dit punt.[2] Als u wordt gevraagd om het x-snijpunt op basis van de grafiek te vinden, is het punt waarschijnlijk exact (bijvoorbeeld op punt 4). Meestal moet u echter een schatting maken van deze methode (het punt bevindt zich bijvoorbeeld tussen 4 en 5). -
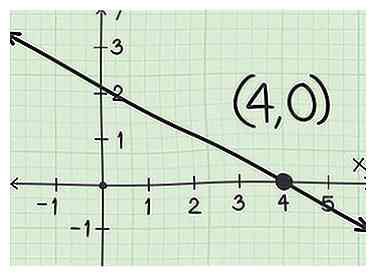 3 Schrijf het geordende paar voor het x-snijpunt. Een besteld paar is in het formulier geschreven en geeft je de coördinaten voor het punt.[3] Het eerste nummer van het paar is het punt waar de lijn de x-as kruist (het x-snijpunt). Het tweede nummer voor zal altijd 0 zijn, omdat een punt op de x-as nooit een waarde voor y zal hebben.[4]
3 Schrijf het geordende paar voor het x-snijpunt. Een besteld paar is in het formulier geschreven en geeft je de coördinaten voor het punt.[3] Het eerste nummer van het paar is het punt waar de lijn de x-as kruist (het x-snijpunt). Het tweede nummer voor zal altijd 0 zijn, omdat een punt op de x-as nooit een waarde voor y zal hebben.[4] - Als een lijn bijvoorbeeld de x-as op punt 4 passeert, is het geordende paar voor het x-snijpunt dat .
Methode twee van drie:
De vergelijking van de lijn gebruiken
-
 1 Bepaal dat de vergelijking van de lijn in standaardvorm is. De standaardvorm van een lineaire vergelijking is .[5] In deze vorm, , , en zijn gehele getallen, en en zijn de coördinaten van een punt op de lijn.
1 Bepaal dat de vergelijking van de lijn in standaardvorm is. De standaardvorm van een lineaire vergelijking is .[5] In deze vorm, , , en zijn gehele getallen, en en zijn de coördinaten van een punt op de lijn. - U kunt bijvoorbeeld de vergelijking krijgen .
-
 2 Sluit 0 in voor . Het x-snijpunt is het punt op de lijn waar de lijn de x-as kruist.[6] Op dit punt is de waarde voor zal 0 zijn.[7] Dus, om het X-snijpunt te vinden, moet je de naar 0 en oplossen voor .
2 Sluit 0 in voor . Het x-snijpunt is het punt op de lijn waar de lijn de x-as kruist.[6] Op dit punt is de waarde voor zal 0 zijn.[7] Dus, om het X-snijpunt te vinden, moet je de naar 0 en oplossen voor . - Bijvoorbeeld als u 0 vervangt voor , je vergelijking ziet er als volgt uit: , dat vereenvoudigt .
-
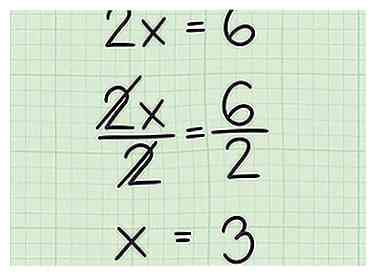 3 Oplossen voor . Om dit te doen, moet u de variabele x isoleren door beide zijden van de vergelijking te delen door de coëfficiënt. Dit geeft je de waarde van wanneer , dat is het x-snijpunt.
3 Oplossen voor . Om dit te doen, moet u de variabele x isoleren door beide zijden van de vergelijking te delen door de coëfficiënt. Dit geeft je de waarde van wanneer , dat is het x-snijpunt. - Bijvoorbeeld:
- Bijvoorbeeld:
-
 4 Schrijf het bestelde paar. Houd er rekening mee dat een besteld paar in het formulier is geschreven . Voor de x-snijpunt, de waarde van is de waarde die u eerder hebt berekend, en de de waarde zal 0 zijn, sinds is altijd gelijk aan 0 op het x-snijpunt.[8]
4 Schrijf het bestelde paar. Houd er rekening mee dat een besteld paar in het formulier is geschreven . Voor de x-snijpunt, de waarde van is de waarde die u eerder hebt berekend, en de de waarde zal 0 zijn, sinds is altijd gelijk aan 0 op het x-snijpunt.[8] - Bijvoorbeeld voor de regel , het x-snijpunt is op het punt .
Methode drie van drie:
De kwadratische formule gebruiken
-
 1 Bepaal dat de vergelijking van de lijn een kwadratische vergelijking is. Een kwadratische vergelijking is een vergelijking die de vorm aanneemt .[9] Een kwadratische vergelijking heeft twee oplossingen, wat betekent dat een regel die in deze vorm wordt geschreven een parabool is en twee x-intercepts zal hebben.[10]
1 Bepaal dat de vergelijking van de lijn een kwadratische vergelijking is. Een kwadratische vergelijking is een vergelijking die de vorm aanneemt .[9] Een kwadratische vergelijking heeft twee oplossingen, wat betekent dat een regel die in deze vorm wordt geschreven een parabool is en twee x-intercepts zal hebben.[10] - Bijvoorbeeld de vergelijking is een kwadratische vergelijking, dus deze regel heeft twee x-onderschept.
-
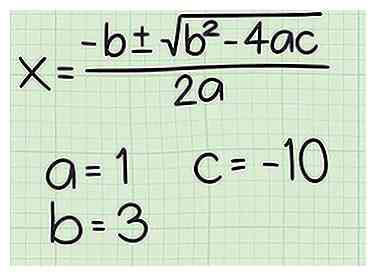 2 Stel de kwadratische formule in. De formule is , waar is gelijk aan de coëfficiënt van de tweede-graads termijn (), is gelijk aan de coëfficiënt van de eerste graad (), en is gelijk aan de constante.[11]
2 Stel de kwadratische formule in. De formule is , waar is gelijk aan de coëfficiënt van de tweede-graads termijn (), is gelijk aan de coëfficiënt van de eerste graad (), en is gelijk aan de constante.[11] -
 3 Sluit alle waarden in de kwadratische formule aan. Zorg ervoor dat u de juiste waarden voor elke variabele vervangt door de vergelijking van de regel.
3 Sluit alle waarden in de kwadratische formule aan. Zorg ervoor dat u de juiste waarden voor elke variabele vervangt door de vergelijking van de regel. - Bijvoorbeeld, als de vergelijking van uw lijn is , je kwadratische formule ziet er als volgt uit: .
-
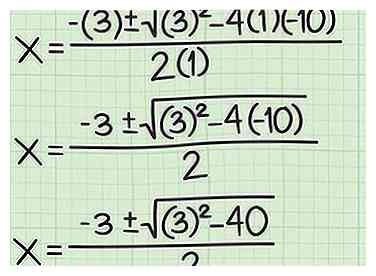 4 Vereenvoudig de vergelijking. Om dit te doen, voltooit u eerst alle vermenigvuldigingen. Zorg ervoor dat u goed let op alle positieve en negatieve tekens.
4 Vereenvoudig de vergelijking. Om dit te doen, voltooit u eerst alle vermenigvuldigingen. Zorg ervoor dat u goed let op alle positieve en negatieve tekens. - Bijvoorbeeld:
- Bijvoorbeeld:
-
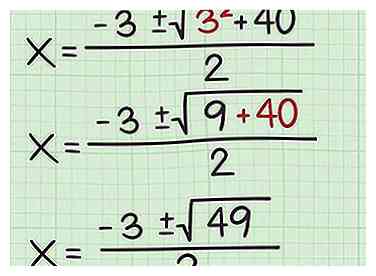 5 Bereken de exponent. Plein de termijn. Voeg vervolgens dit nummer toe aan het andere nummer onder het vierkantswortelbord.
5 Bereken de exponent. Plein de termijn. Voeg vervolgens dit nummer toe aan het andere nummer onder het vierkantswortelbord. - Bijvoorbeeld:
- Bijvoorbeeld:
-
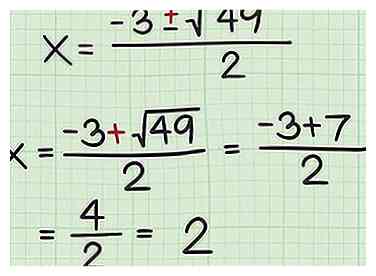 6 Los op voor de optelformule. Omdat de kwadratische formule een , je lost een keer op door toe te voegen en eenmaal door af te trekken. Oplossen door toevoegen geeft je de eerste waarde.
6 Los op voor de optelformule. Omdat de kwadratische formule een , je lost een keer op door toe te voegen en eenmaal door af te trekken. Oplossen door toevoegen geeft je de eerste waarde. - Bijvoorbeeld:
- Bijvoorbeeld:
-
 7 Los op voor de aftrekformule. Dit geeft je de tweede waarde voor . Bereken eerst de vierkantswortel en vind het verschil in de teller. Splits tenslotte door 2.
7 Los op voor de aftrekformule. Dit geeft je de tweede waarde voor . Bereken eerst de vierkantswortel en vind het verschil in de teller. Splits tenslotte door 2. - Bijvoorbeeld:
- Bijvoorbeeld:
-
 8 Zoek de geordende paren voor het x-snijpunt. Vergeet niet dat een geordend paar eerst de x-coördinaat geeft, daarna de y-coördinaat . De waarden zijn de waarden die u hebt berekend met behulp van de kwadratische formule. De waarde is 0, omdat op het x-snijpunt, altijd gelijk aan 0.[12]
8 Zoek de geordende paren voor het x-snijpunt. Vergeet niet dat een geordend paar eerst de x-coördinaat geeft, daarna de y-coördinaat . De waarden zijn de waarden die u hebt berekend met behulp van de kwadratische formule. De waarde is 0, omdat op het x-snijpunt, altijd gelijk aan 0.[12] - Bijvoorbeeld voor de regel , de x-intercepts zijn op punten en .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Identificeer de x-as. Een coördinaatgrafiek heeft een y-as en een x-as. De x-as is de horizontale lijn (de lijn die van links naar rechts loopt). De y-as is de verticale lijn (de lijn die omhoog en omlaag gaat).[1] Het is belangrijk om te kijken naar de x-as bij het lokaliseren van het x-snijpunt.
1 Identificeer de x-as. Een coördinaatgrafiek heeft een y-as en een x-as. De x-as is de horizontale lijn (de lijn die van links naar rechts loopt). De y-as is de verticale lijn (de lijn die omhoog en omlaag gaat).[1] Het is belangrijk om te kijken naar de x-as bij het lokaliseren van het x-snijpunt.  2 Zoek het punt waar de lijn de x-as kruist. Het X-snijpunt is dit punt.[2] Als u wordt gevraagd om het x-snijpunt op basis van de grafiek te vinden, is het punt waarschijnlijk exact (bijvoorbeeld op punt 4). Meestal moet u echter een schatting maken van deze methode (het punt bevindt zich bijvoorbeeld tussen 4 en 5).
2 Zoek het punt waar de lijn de x-as kruist. Het X-snijpunt is dit punt.[2] Als u wordt gevraagd om het x-snijpunt op basis van de grafiek te vinden, is het punt waarschijnlijk exact (bijvoorbeeld op punt 4). Meestal moet u echter een schatting maken van deze methode (het punt bevindt zich bijvoorbeeld tussen 4 en 5).  3 Schrijf het geordende paar voor het x-snijpunt. Een besteld paar is in het formulier geschreven
3 Schrijf het geordende paar voor het x-snijpunt. Een besteld paar is in het formulier geschreven  1 Bepaal dat de vergelijking van de lijn in standaardvorm is. De standaardvorm van een lineaire vergelijking is
1 Bepaal dat de vergelijking van de lijn in standaardvorm is. De standaardvorm van een lineaire vergelijking is  2 Sluit 0 in voor
2 Sluit 0 in voor 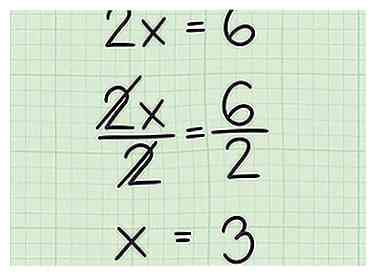 3 Oplossen voor
3 Oplossen voor  4 Schrijf het bestelde paar. Houd er rekening mee dat een besteld paar in het formulier is geschreven
4 Schrijf het bestelde paar. Houd er rekening mee dat een besteld paar in het formulier is geschreven  1 Bepaal dat de vergelijking van de lijn een kwadratische vergelijking is. Een kwadratische vergelijking is een vergelijking die de vorm aanneemt
1 Bepaal dat de vergelijking van de lijn een kwadratische vergelijking is. Een kwadratische vergelijking is een vergelijking die de vorm aanneemt 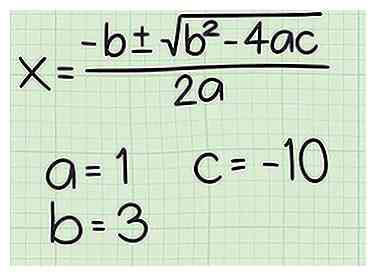 2 Stel de kwadratische formule in. De formule is
2 Stel de kwadratische formule in. De formule is  3 Sluit alle waarden in de kwadratische formule aan. Zorg ervoor dat u de juiste waarden voor elke variabele vervangt door de vergelijking van de regel.
3 Sluit alle waarden in de kwadratische formule aan. Zorg ervoor dat u de juiste waarden voor elke variabele vervangt door de vergelijking van de regel. 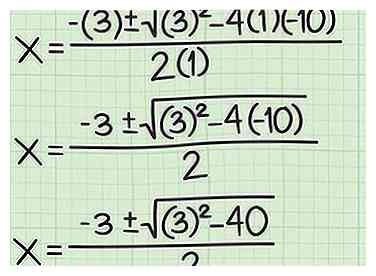 4 Vereenvoudig de vergelijking. Om dit te doen, voltooit u eerst alle vermenigvuldigingen. Zorg ervoor dat u goed let op alle positieve en negatieve tekens.
4 Vereenvoudig de vergelijking. Om dit te doen, voltooit u eerst alle vermenigvuldigingen. Zorg ervoor dat u goed let op alle positieve en negatieve tekens. 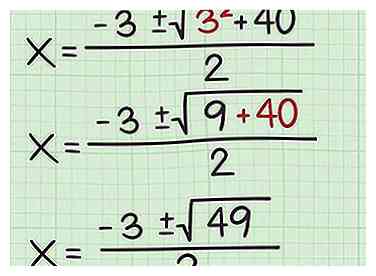 5 Bereken de exponent. Plein de
5 Bereken de exponent. Plein de 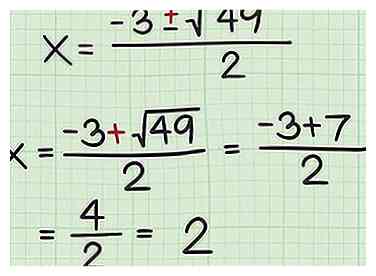 6 Los op voor de optelformule. Omdat de kwadratische formule een
6 Los op voor de optelformule. Omdat de kwadratische formule een  7 Los op voor de aftrekformule. Dit geeft je de tweede waarde voor
7 Los op voor de aftrekformule. Dit geeft je de tweede waarde voor  8 Zoek de geordende paren voor het x-snijpunt. Vergeet niet dat een geordend paar eerst de x-coördinaat geeft, daarna de y-coördinaat
8 Zoek de geordende paren voor het x-snijpunt. Vergeet niet dat een geordend paar eerst de x-coördinaat geeft, daarna de y-coördinaat