Om verschillende redenen moet u misschien de maximum- of minimumwaarde van een geselecteerde kwadratische functie kunnen definiëren. Je kunt het maximum of minimum vinden als je originele functie in algemene vorm is geschreven, of in standaardvorm, . Ten slotte kunt u ook wat basisberekeningen gebruiken om het maximum of minimum van een kwadratische functie te definiëren.
Methode één van de drie:
Beginnen met de algemene vorm van de functie
-
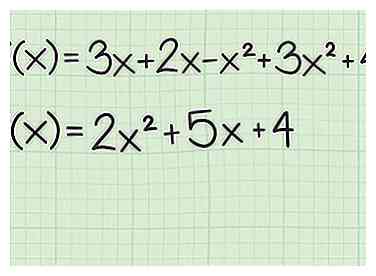 1 Stel de functie in algemene vorm in. Een kwadratische functie is er een met een termijn. Het kan al dan niet een bevatten term zonder een exponent. Er zijn geen exponenten groter dan 2. Het algemene formulier is . Combineer, indien nodig, vergelijkbare termen en herschik om de functie in deze algemene vorm in te stellen.[1]
1 Stel de functie in algemene vorm in. Een kwadratische functie is er een met een termijn. Het kan al dan niet een bevatten term zonder een exponent. Er zijn geen exponenten groter dan 2. Het algemene formulier is . Combineer, indien nodig, vergelijkbare termen en herschik om de functie in deze algemene vorm in te stellen.[1] - Stel dat u begint met . Combineer de voorwaarden en de voorwaarden om het volgende in algemene vorm te krijgen:
- Stel dat u begint met . Combineer de voorwaarden en de voorwaarden om het volgende in algemene vorm te krijgen:
-
 2 Bepaal de richting van de grafiek. Een kwadratische functie resulteert in de grafiek van een parabool. De parabool opent ofwel naar boven of naar beneden. Als , de coëfficiënt van de termijn, is positief, dan opent de parabool zich naar boven. Als is negatief, dan opent de parabool naar beneden. Bekijk de volgende voorbeelden:[2]
2 Bepaal de richting van de grafiek. Een kwadratische functie resulteert in de grafiek van een parabool. De parabool opent ofwel naar boven of naar beneden. Als , de coëfficiënt van de termijn, is positief, dan opent de parabool zich naar boven. Als is negatief, dan opent de parabool naar beneden. Bekijk de volgende voorbeelden:[2] - Voor , dus de parabool opent naar boven.
- Voor , dus de parabool opent naar beneden.
- Voor , dus de parabool opent naar boven.
- Als de parabool zich naar boven opent, zult u de minimumwaarde ervan vinden. Als de parabool naar beneden opent, vindt u de maximale waarde.
-
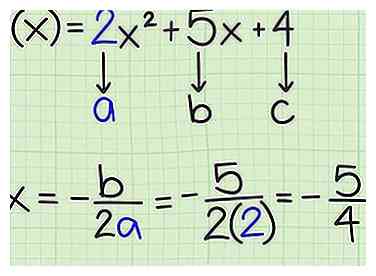 3 Bereken -b / 2a. De waarde van vertelt je het waarde van de top van de parabool. Wanneer de kwadratische functie is geschreven in de algemene vorm van , gebruik de coëfficiënten van de en voorwaarden als volgt:
3 Bereken -b / 2a. De waarde van vertelt je het waarde van de top van de parabool. Wanneer de kwadratische functie is geschreven in de algemene vorm van , gebruik de coëfficiënten van de en voorwaarden als volgt: - Voor een functie , en . Zoek daarom de x-waarde van de vertex als:
- Neem als tweede voorbeeld de functie in overweging . In dit voorbeeld en . Zoek daarom de x-waarde van de vertex als:
- Voor een functie , en . Zoek daarom de x-waarde van de vertex als:
-
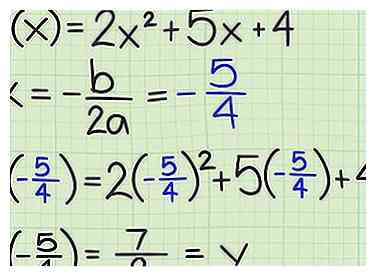 4 Zoek de bijbehorende f (x) -waarde. Voer de waarde van x in die u zojuist in de functie hebt berekend om de bijbehorende waarde van f (x) te vinden. Dit is het minimum of maximum van de functie.
4 Zoek de bijbehorende f (x) -waarde. Voer de waarde van x in die u zojuist in de functie hebt berekend om de bijbehorende waarde van f (x) te vinden. Dit is het minimum of maximum van de functie. - Voor het eerste voorbeeld hierboven, , je hebt de x-waarde berekend voor de vertex die moet zijn . invoeren in plaats van in de functie om de maximale waarde te vinden:
- Voor het tweede voorbeeld hierboven, , je hebt de vertex gevonden waar je bent . invoegen in plaats van in de functie om de maximale waarde te vinden:
- Voor het eerste voorbeeld hierboven, , je hebt de x-waarde berekend voor de vertex die moet zijn . invoeren in plaats van in de functie om de maximale waarde te vinden:
-
 5 Rapporteer uw resultaten. Bekijk de vraag die u is gesteld. Als u om de coördinaten van de vertex wordt gevraagd, moet u beide rapporteren en (of ) waarden. Als u alleen om het maximum of minimum wordt gevraagd, hoeft u alleen de (of ) waarde. Refereer naar de waarde van de coëfficiënt om zeker te zijn of u een maximum of een minimum hebt.
5 Rapporteer uw resultaten. Bekijk de vraag die u is gesteld. Als u om de coördinaten van de vertex wordt gevraagd, moet u beide rapporteren en (of ) waarden. Als u alleen om het maximum of minimum wordt gevraagd, hoeft u alleen de (of ) waarde. Refereer naar de waarde van de coëfficiënt om zeker te zijn of u een maximum of een minimum hebt. - Voor het eerste voorbeeld , de waarde van is positief, dus meldt u de minimumwaarde. De vertex is op en de minimumwaarde is .
- Voor het tweede voorbeeld, , de waarde van is negatief, dus rapporteert u de maximale waarde. De vertex is op en de maximale waarde is .
Methode twee van drie:
Het standaard- of vertex-formulier gebruiken
-
 1 Schrijf uw kwadratische functie in standaard- of vertexvorm. De standaardvorm van een algemene kwadratische functie, die ook de vertex-vorm kan worden genoemd, ziet er als volgt uit:[3]
1 Schrijf uw kwadratische functie in standaard- of vertexvorm. De standaardvorm van een algemene kwadratische functie, die ook de vertex-vorm kan worden genoemd, ziet er als volgt uit:[3] - Als uw functie al in dit formulier aan u is gegeven, hoeft u alleen de variabelen te herkennen , en . Als uw functie begint in de algemene vorm , je moet het vierkant invullen om het in vertex-vorm te herschrijven.
- Zie Voltooi het vierkant om te bekijken hoe het vierkant moet worden voltooid.
-
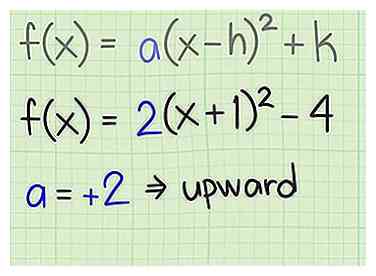 2 Bepaal de richting van de grafiek. Net als met een kwadratische functie geschreven in zijn algemene vorm, kun je de richting van de parabool bepalen door naar de coëfficiënt te kijken . Als in deze standaardvorm is positief, dan opent de parabool naar boven. Als is negatief, dan opent de parabool naar beneden. Bekijk de volgende voorbeelden:[4]
2 Bepaal de richting van de grafiek. Net als met een kwadratische functie geschreven in zijn algemene vorm, kun je de richting van de parabool bepalen door naar de coëfficiënt te kijken . Als in deze standaardvorm is positief, dan opent de parabool naar boven. Als is negatief, dan opent de parabool naar beneden. Bekijk de volgende voorbeelden:[4] - Voor , , wat positief is, dus opent de parabool omhoog.
- Voor , , wat negatief is, dus opent de parabool naar beneden.
- Als de parabool zich naar boven opent, zult u de minimumwaarde ervan vinden. Als de parabool naar beneden opent, vindt u de maximale waarde.
-
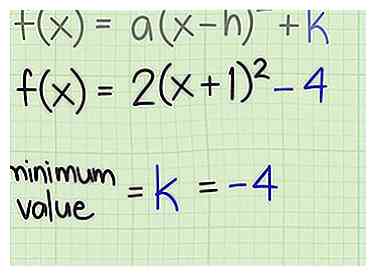 3 Identificeer de minimum- of maximumwaarde. Wanneer de functie in standaardvorm is geschreven, is het vinden van de minimum- of maximumwaarde zo eenvoudig als het aangeven van de waarde van de variabele . Voor de twee hierboven gegeven voorbeeldfuncties zijn deze waarden:
3 Identificeer de minimum- of maximumwaarde. Wanneer de functie in standaardvorm is geschreven, is het vinden van de minimum- of maximumwaarde zo eenvoudig als het aangeven van de waarde van de variabele . Voor de twee hierboven gegeven voorbeeldfuncties zijn deze waarden: - Voor , . Dit is de minimumwaarde van de functie omdat deze parabool naar boven opent.
- Voor , . Dit is de maximale waarde van de functie, omdat deze parabool naar beneden opent.
-
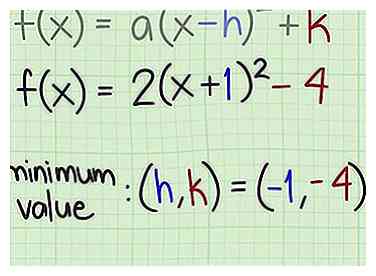 4 Vind de vertex. Als u om de coördinaten van de minimum- of maximumwaarde wordt gevraagd, is het punt . Merk echter op dat in de standaardvorm van de vergelijking de term tussen de haakjes staat , dus je hebt het tegenovergestelde teken nodig van het nummer dat volgt op de .
4 Vind de vertex. Als u om de coördinaten van de minimum- of maximumwaarde wordt gevraagd, is het punt . Merk echter op dat in de standaardvorm van de vergelijking de term tussen de haakjes staat , dus je hebt het tegenovergestelde teken nodig van het nummer dat volgt op de . - Voor , de term tussen haakjes is (x + 1), die herschreven kan worden als (x - (- 1)). Dus, . Daarom zijn de coördinaten van de vertex voor deze functie .
- Voor , de term tussen haakjes is (x-2). daarom . De coördinaten van de vertex zijn (2, 2).
Methode drie van drie:
Calculus gebruiken om het minimum of maximum af te leiden
-
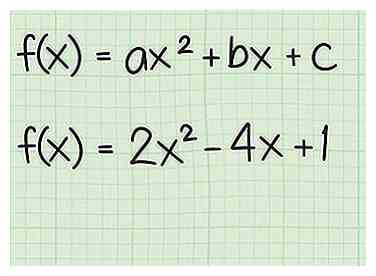 1 Begin met het algemene formulier. Schrijf je kwadratische functie in algemene vorm op, . Indien nodig, moet u dergelijke termen combineren en herschikken om de juiste vorm te krijgen.[5]
1 Begin met het algemene formulier. Schrijf je kwadratische functie in algemene vorm op, . Indien nodig, moet u dergelijke termen combineren en herschikken om de juiste vorm te krijgen.[5] - Begin met de voorbeeldfunctie .
-
 2 Gebruik de machtsregel om de eerste afgeleide te vinden. Met behulp van de basis eerstejaars calculus, kun je de eerste afgeleide van de algemene kwadratische functie vinden .[6]
2 Gebruik de machtsregel om de eerste afgeleide te vinden. Met behulp van de basis eerstejaars calculus, kun je de eerste afgeleide van de algemene kwadratische functie vinden .[6] - Voor de voorbeeldfunctie , vind de afgeleide als:
- Voor de voorbeeldfunctie , vind de afgeleide als:
-
 3 Stel de afgeleide gelijk aan nul. Herinner dat de afgeleide van een functie u de helling van de functie op dat geselecteerde punt vertelt. Het minimum of maximum van een functie treedt op wanneer de helling nul is. Daarom, om te bepalen waar het minimum of maximum optreedt, stelt u de afgeleide gelijk aan nul. Ga door met het voorbeeldprobleem van boven:[7]
3 Stel de afgeleide gelijk aan nul. Herinner dat de afgeleide van een functie u de helling van de functie op dat geselecteerde punt vertelt. Het minimum of maximum van een functie treedt op wanneer de helling nul is. Daarom, om te bepalen waar het minimum of maximum optreedt, stelt u de afgeleide gelijk aan nul. Ga door met het voorbeeldprobleem van boven:[7] -
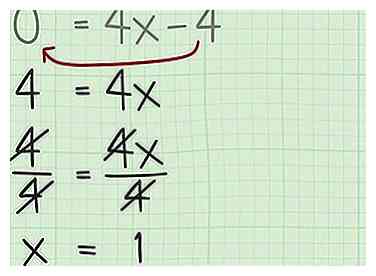 4 Los op voor X. Gebruik basisregels van de algebra om de functie opnieuw in te delen en de waarde voor x op te lossen, wanneer het derivaat gelijk is aan nul. Deze oplossing vertelt u de x-coördinaat van de top van de functie, waar het maximum of minimum zal optreden.[8]
4 Los op voor X. Gebruik basisregels van de algebra om de functie opnieuw in te delen en de waarde voor x op te lossen, wanneer het derivaat gelijk is aan nul. Deze oplossing vertelt u de x-coördinaat van de top van de functie, waar het maximum of minimum zal optreden.[8] -
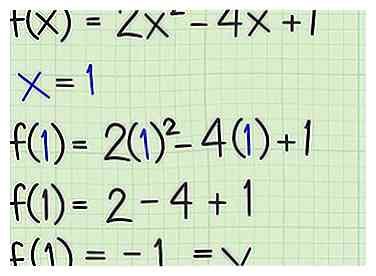 5 Voeg de opgeloste waarde van x in de originele functie in. De minimum- of maximumwaarde van de functie is de waarde voor bij de geselecteerde positie. Voer uw waarde in van in de originele functie en los op om het minimum of maximum te vinden.[9]
5 Voeg de opgeloste waarde van x in de originele functie in. De minimum- of maximumwaarde van de functie is de waarde voor bij de geselecteerde positie. Voer uw waarde in van in de originele functie en los op om het minimum of maximum te vinden.[9] - Voor de functie op ,
- Voor de functie op ,
-
 6 Rapporteer uw oplossing. De oplossing geeft u de top van het maximale of minimale punt. Voor deze voorbeeldfunctie, , de vertex treedt op bij . De coëfficiënt is positief, dus de functie opent naar boven. Daarom is de minimumwaarde van de functie de y-coördinaat van de vertex, wat is .[10]
6 Rapporteer uw oplossing. De oplossing geeft u de top van het maximale of minimale punt. Voor deze voorbeeldfunctie, , de vertex treedt op bij . De coëfficiënt is positief, dus de functie opent naar boven. Daarom is de minimumwaarde van de functie de y-coördinaat van de vertex, wat is .[10]
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
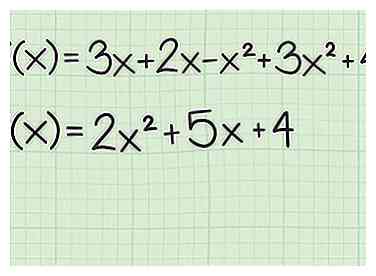 1 Stel de functie in algemene vorm in. Een kwadratische functie is er een met een
1 Stel de functie in algemene vorm in. Een kwadratische functie is er een met een  2 Bepaal de richting van de grafiek. Een kwadratische functie resulteert in de grafiek van een parabool. De parabool opent ofwel naar boven of naar beneden. Als
2 Bepaal de richting van de grafiek. Een kwadratische functie resulteert in de grafiek van een parabool. De parabool opent ofwel naar boven of naar beneden. Als 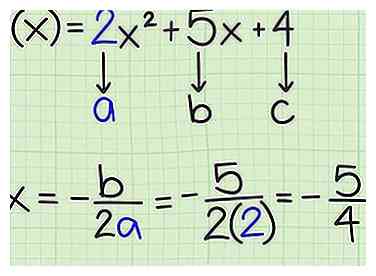 3 Bereken -b / 2a. De waarde van
3 Bereken -b / 2a. De waarde van 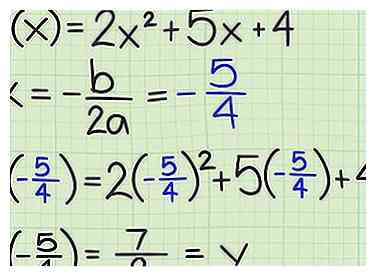 4 Zoek de bijbehorende f (x) -waarde. Voer de waarde van x in die u zojuist in de functie hebt berekend om de bijbehorende waarde van f (x) te vinden. Dit is het minimum of maximum van de functie.
4 Zoek de bijbehorende f (x) -waarde. Voer de waarde van x in die u zojuist in de functie hebt berekend om de bijbehorende waarde van f (x) te vinden. Dit is het minimum of maximum van de functie.  5 Rapporteer uw resultaten. Bekijk de vraag die u is gesteld. Als u om de coördinaten van de vertex wordt gevraagd, moet u beide rapporteren
5 Rapporteer uw resultaten. Bekijk de vraag die u is gesteld. Als u om de coördinaten van de vertex wordt gevraagd, moet u beide rapporteren  1 Schrijf uw kwadratische functie in standaard- of vertexvorm. De standaardvorm van een algemene kwadratische functie, die ook de vertex-vorm kan worden genoemd, ziet er als volgt uit:[3]
1 Schrijf uw kwadratische functie in standaard- of vertexvorm. De standaardvorm van een algemene kwadratische functie, die ook de vertex-vorm kan worden genoemd, ziet er als volgt uit:[3] 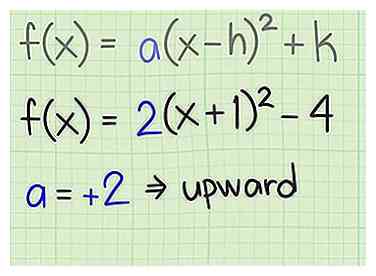 2 Bepaal de richting van de grafiek. Net als met een kwadratische functie geschreven in zijn algemene vorm, kun je de richting van de parabool bepalen door naar de coëfficiënt te kijken
2 Bepaal de richting van de grafiek. Net als met een kwadratische functie geschreven in zijn algemene vorm, kun je de richting van de parabool bepalen door naar de coëfficiënt te kijken 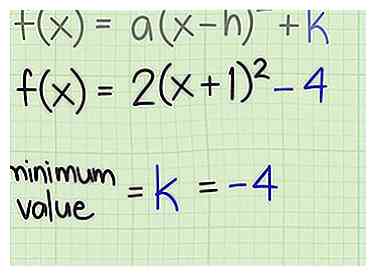 3 Identificeer de minimum- of maximumwaarde. Wanneer de functie in standaardvorm is geschreven, is het vinden van de minimum- of maximumwaarde zo eenvoudig als het aangeven van de waarde van de variabele
3 Identificeer de minimum- of maximumwaarde. Wanneer de functie in standaardvorm is geschreven, is het vinden van de minimum- of maximumwaarde zo eenvoudig als het aangeven van de waarde van de variabele 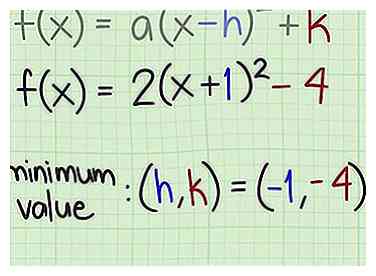 4 Vind de vertex. Als u om de coördinaten van de minimum- of maximumwaarde wordt gevraagd, is het punt
4 Vind de vertex. Als u om de coördinaten van de minimum- of maximumwaarde wordt gevraagd, is het punt 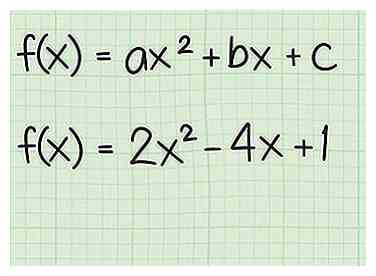 1 Begin met het algemene formulier. Schrijf je kwadratische functie in algemene vorm op,
1 Begin met het algemene formulier. Schrijf je kwadratische functie in algemene vorm op,  2 Gebruik de machtsregel om de eerste afgeleide te vinden. Met behulp van de basis eerstejaars calculus, kun je de eerste afgeleide van de algemene kwadratische functie vinden
2 Gebruik de machtsregel om de eerste afgeleide te vinden. Met behulp van de basis eerstejaars calculus, kun je de eerste afgeleide van de algemene kwadratische functie vinden  3 Stel de afgeleide gelijk aan nul. Herinner dat de afgeleide van een functie u de helling van de functie op dat geselecteerde punt vertelt. Het minimum of maximum van een functie treedt op wanneer de helling nul is. Daarom, om te bepalen waar het minimum of maximum optreedt, stelt u de afgeleide gelijk aan nul. Ga door met het voorbeeldprobleem van boven:[7]
3 Stel de afgeleide gelijk aan nul. Herinner dat de afgeleide van een functie u de helling van de functie op dat geselecteerde punt vertelt. Het minimum of maximum van een functie treedt op wanneer de helling nul is. Daarom, om te bepalen waar het minimum of maximum optreedt, stelt u de afgeleide gelijk aan nul. Ga door met het voorbeeldprobleem van boven:[7] 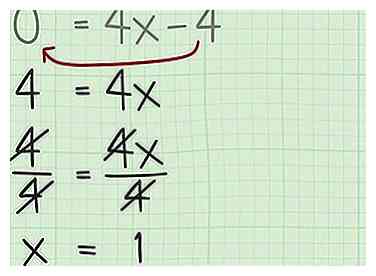 4 Los op voor X. Gebruik basisregels van de algebra om de functie opnieuw in te delen en de waarde voor x op te lossen, wanneer het derivaat gelijk is aan nul. Deze oplossing vertelt u de x-coördinaat van de top van de functie, waar het maximum of minimum zal optreden.[8]
4 Los op voor X. Gebruik basisregels van de algebra om de functie opnieuw in te delen en de waarde voor x op te lossen, wanneer het derivaat gelijk is aan nul. Deze oplossing vertelt u de x-coördinaat van de top van de functie, waar het maximum of minimum zal optreden.[8] 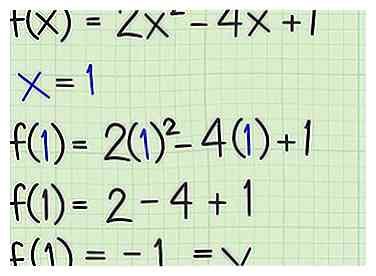 5 Voeg de opgeloste waarde van x in de originele functie in. De minimum- of maximumwaarde van de functie is de waarde voor
5 Voeg de opgeloste waarde van x in de originele functie in. De minimum- of maximumwaarde van de functie is de waarde voor  6 Rapporteer uw oplossing. De oplossing geeft u de top van het maximale of minimale punt. Voor deze voorbeeldfunctie,
6 Rapporteer uw oplossing. De oplossing geeft u de top van het maximale of minimale punt. Voor deze voorbeeldfunctie,