Een trinominale is een algebraïsche uitdrukking die bestaat uit drie termen. Hoogstwaarschijnlijk begint u te leren factorfactoren vierkant trinomials, dat wil zeggen trinomialen geschreven in de vormbijl2 + bx + c. Er zijn verschillende trucs om te leren die van toepassing zijn op verschillende soorten kwadratische trinominale, maar je zult beter en sneller worden in het gebruik ervan met oefenen. Polynomen van hogere graden, met termen zoals x3 of x4, zijn niet altijd op dezelfde manier oplosbaar, maar je kunt vaak eenvoudige factoring of substitutie gebruiken om ze om te zetten in problemen die kunnen worden opgelost zoals elke kwadratische formule.
Methode één van de drie:
Factoren x2 + bx + c
-
 1 Leer FOIL-vermenigvuldiging. Je hebt misschien al de FOIL-methode geleerd, of "Eerst, Buiten, Binnen, Laatste," om uitdrukkingen zoals (x + 2) (x + 4) te vermenigvuldigen. Het is handig om te weten hoe dit werkt voordat we tot factoring komen:
1 Leer FOIL-vermenigvuldiging. Je hebt misschien al de FOIL-methode geleerd, of "Eerst, Buiten, Binnen, Laatste," om uitdrukkingen zoals (x + 2) (x + 4) te vermenigvuldigen. Het is handig om te weten hoe dit werkt voordat we tot factoring komen: - Vermenigvuldig de Eerste voorwaarden: (X+2)(X+4) = X2 + __
- Vermenigvuldig de Buiten voorwaarden: (X2) (x +4) = x2+4x + __
- Vermenigvuldig de Binnen voorwaarden: (x +2)(X+4) = x2+ 4x +2x + __
- Vermenigvuldig de Laatste voorwaarden: (x +2) (X +4) = x2+ 4x + 2x +8
- Vereenvoudig: x2+4x + 2x+8 = x2+6x+8
-
 2 Begrijp factoring. Wanneer u twee binomials samen vermenigvuldigt in de FOL-methode, krijgt u een trinominaal (een uitdrukking met drie termen) in de vorm eenX2+bx +c, waar a, b en c gewone nummers zijn. Als je begint met een vergelijking in dezelfde vorm, kun je het terug in twee binomials factoreren.
2 Begrijp factoring. Wanneer u twee binomials samen vermenigvuldigt in de FOL-methode, krijgt u een trinominaal (een uitdrukking met drie termen) in de vorm eenX2+bx +c, waar a, b en c gewone nummers zijn. Als je begint met een vergelijking in dezelfde vorm, kun je het terug in twee binomials factoreren. - Als de vergelijking niet in deze volgorde is geschreven, verplaatst u de voorwaarden daaromheen. Herschrijf bijvoorbeeld 3x - 10 + x2 als X2 + 3x - 10.
- Omdat de hoogste exponent 2 is (x2, dit type expressie is "kwadratisch".
-
 3 Schrijf een spatie voor het antwoord in FOIL-vorm. Schrijf voor nu (__ __)(__ __) in de ruimte waar je het antwoord schrijft. We zullen dit invullen als we gaan.
3 Schrijf een spatie voor het antwoord in FOIL-vorm. Schrijf voor nu (__ __)(__ __) in de ruimte waar je het antwoord schrijft. We zullen dit invullen als we gaan. - Schrijf nog geen + of - tussen de lege termen, omdat we niet weten wat het zal zijn.
-
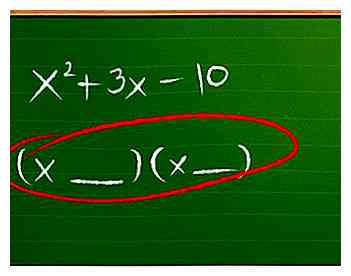 4 Vul de eerste voorwaarden in. Voor eenvoudige problemen, waarbij de eerste term van je trinominaal slechts x is2, de termen in de eerste positie zullen dat altijd zijn X en X. Dit zijn de factoren van de term x2, sinds x keer x = x2.
4 Vul de eerste voorwaarden in. Voor eenvoudige problemen, waarbij de eerste term van je trinominaal slechts x is2, de termen in de eerste positie zullen dat altijd zijn X en X. Dit zijn de factoren van de term x2, sinds x keer x = x2. - Ons voorbeeld x2 + 3x - 10 begint net met x2, dus we kunnen schrijven:
- (x __) (x __)
- We zullen ingewikkelder problemen behandelen in de volgende sectie, inclusief trinominaties die beginnen met een term als 6x2 of -x2. Volg voorlopig het voorbeeldprobleem.
-
 5 Gebruik factoring om naar de laatste termen te raden. Als je teruggaat en de stap van de FOIL-methode opnieuw leest, zul je zien dat het vermenigvuldigen van de laatste termen samen de laatste term in de polynoom geeft (de ene zonder x). Dus voor factor, we moeten twee nummers vinden vermenigvuldigen om de laatste term te vormen.
5 Gebruik factoring om naar de laatste termen te raden. Als je teruggaat en de stap van de FOIL-methode opnieuw leest, zul je zien dat het vermenigvuldigen van de laatste termen samen de laatste term in de polynoom geeft (de ene zonder x). Dus voor factor, we moeten twee nummers vinden vermenigvuldigen om de laatste term te vormen. - In ons voorbeeld x2 + 3x - 10, de laatste term is -10.
- Wat zijn de factoren van -10? Welke twee getallen vermenigvuldigd samen gelijk -10?
- Er zijn een paar mogelijkheden: -1 keer 10, 1 keer -10, -2 keer 5 of 2 keer -5. Schrijf deze paren ergens neer om ze te onthouden.
- Wijzig ons antwoord nog niet. Het ziet er nog steeds als volgt uit: (x __) (x __).
-
 6 Test welke mogelijkheden werken met vermenigvuldiging van buiten en van binnen. We hebben de laatste termen beperkt tot enkele mogelijkheden. Gebruik vallen en opstaan om elke mogelijkheid te testen, vermenigvuldig de termen Buiten en Binnen en vergelijk het resultaat met onze trinominaal. Bijvoorbeeld:
6 Test welke mogelijkheden werken met vermenigvuldiging van buiten en van binnen. We hebben de laatste termen beperkt tot enkele mogelijkheden. Gebruik vallen en opstaan om elke mogelijkheid te testen, vermenigvuldig de termen Buiten en Binnen en vergelijk het resultaat met onze trinominaal. Bijvoorbeeld: - Ons oorspronkelijke probleem heeft een "x" -term van 3x, dus dat is waar we in deze test mee willen eindigen.
- Test -1 en 10: (x-1) (x + 10). De buitenkant + binnenkant = 10x - x = 9x. Nee.
- Test 1 en -10: (x + 1) (x-10). -10x + x = -9x. Dat klopt niet. Als je eenmaal -1 en 10 hebt getest, weet je dat 1 en -10 precies het tegenovergestelde zijn van het bovenstaande antwoord: -9x in plaats van 9x.
- Test -2 en 5: (x-2) (x + 5). 5x - 2x = 3x. Dat komt overeen met het oorspronkelijke polynoom, dus dit is het juiste antwoord: (X-2) (x + 5).
- In eenvoudige gevallen als deze, als je geen constante voor de x hebt2 termijn, kunt u een snelkoppeling gebruiken: voeg gewoon de twee factoren bij elkaar en plaats er een "x" achter (-2 + 5 → 3x). Dit zal echter niet werken voor ingewikkelder problemen, dus het is goed om de "lange weg" zoals hierboven beschreven te onthouden.
Methode twee van drie:
Meer gecompliceerde Trinomials factoren
-
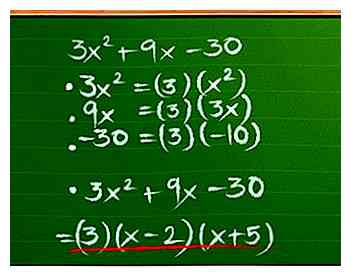 1 Gebruik eenvoudige factoring om gecompliceerdere problemen eenvoudiger te maken. Laten we zeggen dat je moet factor 3x2 + 9x - 30. Zoek naar iets dat bijdraagt aan elk van de drie termen (de "grootste gemene deler" of GCF).[1] In dit geval is het 3:
1 Gebruik eenvoudige factoring om gecompliceerdere problemen eenvoudiger te maken. Laten we zeggen dat je moet factor 3x2 + 9x - 30. Zoek naar iets dat bijdraagt aan elk van de drie termen (de "grootste gemene deler" of GCF).[1] In dit geval is het 3: - 3x2 = (3) (x2)
- 9x = (3) (3x)
- -30 = (3)(-10)
- Daarom 3x2 + 9x - 30 = (3) (x2+ 3x-10). We kunnen de nieuwe trinominale factor weglaten met behulp van de stappen in het bovenstaande gedeelte. Ons laatste antwoord zal zijn (3) (x-2) (x + 5).
-
 2 Zoek naar lastiger factoren. Soms kan de factor variabelen omvatten, of het kan een paar keer nodig zijn om een factor te berekenen om de eenvoudigst mogelijke uitdrukking te vinden. Hier zijn een paar voorbeelden:
2 Zoek naar lastiger factoren. Soms kan de factor variabelen omvatten, of het kan een paar keer nodig zijn om een factor te berekenen om de eenvoudigst mogelijke uitdrukking te vinden. Hier zijn een paar voorbeelden: - 2x2y + 14xy + 24y = (2y)(X2 + 7x + 12)
- X4 + 11x3 - 26x2 = (X2)(X2 + 11x - 26)
- -X2 + 6x - 9 = (-1)(X2 - 6x + 9)
- Vergeet niet om de nieuwe trinomiaal verder te bepalen met behulp van de stappen in methode 1. Controleer uw werk en vind vergelijkbare voorbeeldproblemen in de voorbeeldproblemen onder aan deze pagina.
-
 3 Los problemen op met een nummer voor de x2. Sommige kwadratische trinomialen kunnen niet worden vereenvoudigd tot het eenvoudigste type probleem. Leer hoe problemen zoals 3x op te lossen2 + 10x + 8, oefen dan alleen, met de voorbeeldproblemen onderaan de pagina:
3 Los problemen op met een nummer voor de x2. Sommige kwadratische trinomialen kunnen niet worden vereenvoudigd tot het eenvoudigste type probleem. Leer hoe problemen zoals 3x op te lossen2 + 10x + 8, oefen dan alleen, met de voorbeeldproblemen onderaan de pagina: - Stel ons antwoord op: (__ __)(__ __)
- Onze "Eerste" voorwaarden hebben elk een x en vermenigvuldigen zich samen om 3x te maken2. Er is slechts één mogelijke optie hier: (3x __) (x __).
- Lijst factoren van 8. Onze opties zijn 1 keer 8, of 2 keer 4.
- Test deze met de termen Buiten en Binnen. Merk op dat de volgorde van de factoren ertoe doet, omdat de Outside-term met 3x wordt vermenigvuldigd in plaats van x. Probeer elke mogelijkheid uit tot je een Outside + Inside-resultaat van 10x behaalt (van het oorspronkelijke probleem):
- (3x + 1) (x + 8) → 24x + x = 25x Nee
- (3x + 8) (x + 1) → 3x + 8x = 11x Nee
- (3x + 2) (x + 4) → 12x + 2x = 14x Nee
- (3x + 4) (x + 2) → 6x + 4x = 10x Ja Dit is de juiste factor.
-
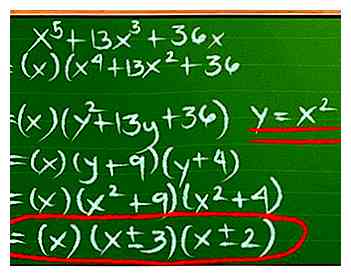 4 Gebruik substitutie voor Trinominals van hogere graden. Je wiskundeboek kan je verrassen met een vergelijking met een hoge exponent, zoals x4, zelfs nadat u eenvoudige factoring hebt gebruikt om het probleem eenvoudiger te maken. Probeer een nieuwe variabele te vervangen die het verandert in een probleem dat u weet op te lossen. Bijvoorbeeld:
4 Gebruik substitutie voor Trinominals van hogere graden. Je wiskundeboek kan je verrassen met een vergelijking met een hoge exponent, zoals x4, zelfs nadat u eenvoudige factoring hebt gebruikt om het probleem eenvoudiger te maken. Probeer een nieuwe variabele te vervangen die het verandert in een probleem dat u weet op te lossen. Bijvoorbeeld: - X5+ 13x3+ 36x
- = (X) (x4+ 13x2+36)
- Laten we een nieuwe variabele verzinnen. We zeggen y = x2en plug het in:
- (X) (y213y + + 36)
- = (X) (y + 9) (y + 4). Schakel nu terug naar het gebruik van de oorspronkelijke variabele:
- = (X) (x29) (x2+4)
- =(X) (x ± 3) (x ± 2)
Methode drie van drie:
Speciale gevallen factoring
-
 1 Controleer op priemgetallen. Controleer om te zien of de constante in de eerste of derde termijn van de trinominale een priemgetal is. Een priemgetal kan alleen gelijkmatig alleen worden gedeeld en 1, dus er is slechts één mogelijk paar binomiale factors.br>
1 Controleer op priemgetallen. Controleer om te zien of de constante in de eerste of derde termijn van de trinominale een priemgetal is. Een priemgetal kan alleen gelijkmatig alleen worden gedeeld en 1, dus er is slechts één mogelijk paar binomiale factors.br> - Bijvoorbeeld in x2 + 6x + 5, "5 is een priemgetal, dus de binomiaal moet de vorm hebben (__ 5) (__ 1).
- In het probleem 3x2+ 10 x + 8, 3 is een priemgetal, dus de binomiaal moet de vorm hebben (3x __) (x __).
- Voor het probleem 3x2+ 4x + 1, beide 3 en 1 zijn priemgetallen, dus de enige mogelijke oplossing is (3x + 1) (x + 1). (Je moet dit nog steeds vermenigvuldigen om je werk te controleren, omdat sommige uitdrukkingen helemaal niet kunnen worden verwerkt - bijvoorbeeld 3x2+ 100x + 1 heeft geen factoren.)
-
 2 Controleer om te zien of de trinominale een perfect vierkant is. Een perfect vierkant trinominaal kan worden verwerkt in twee identieke binomials, en de factor wordt meestal geschreven (x + 1)2 in plaats van (x + 1) (x + 1). Hier een paar veel voorkomende die de neiging hebben om in problemen te verschijnen:
2 Controleer om te zien of de trinominale een perfect vierkant is. Een perfect vierkant trinominaal kan worden verwerkt in twee identieke binomials, en de factor wordt meestal geschreven (x + 1)2 in plaats van (x + 1) (x + 1). Hier een paar veel voorkomende die de neiging hebben om in problemen te verschijnen: - X2+ 2x + 1 = (x + 1)2en x2-2x + 1 = (x-1)2
- X2+ 4x + 4 = (x + 2)2en x2-4x + 4 = (x-2)2
- X26x + + 9 = (x + 3)2en x2-6x + 9 = (x-3)2
- Een perfect vierkant trinominaal in de vorm eenX2 + bx + c heeft altijd gedaan een en c termen die positieve perfecte vierkanten zijn (zoals 1, 4, 9, 16 of 25), en a b term (positief of negatief) die gelijk is aan 2 (√a * √c).[2]
-
 3 Controleer of er geen oplossing bestaat. Niet alle trinomialen kunnen worden verwerkt. Als je vastzit aan een kwadratische drievoudigheid (bijl2+ bx + c), gebruik de kwadratische formule om het antwoord te vinden. Als de enige antwoorden de vierkantswortel van een negatief getal zijn, bestaan er geen echte oplossingen, dus er zijn geen factoren.
3 Controleer of er geen oplossing bestaat. Niet alle trinomialen kunnen worden verwerkt. Als je vastzit aan een kwadratische drievoudigheid (bijl2+ bx + c), gebruik de kwadratische formule om het antwoord te vinden. Als de enige antwoorden de vierkantswortel van een negatief getal zijn, bestaan er geen echte oplossingen, dus er zijn geen factoren. - Gebruik voor niet-quadratische trinomialen het Criterium van Eisenstein, beschreven in de sectie Tips.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Leer FOIL-vermenigvuldiging. Je hebt misschien al de FOIL-methode geleerd, of "Eerst, Buiten, Binnen, Laatste," om uitdrukkingen zoals (x + 2) (x + 4) te vermenigvuldigen. Het is handig om te weten hoe dit werkt voordat we tot factoring komen:
1 Leer FOIL-vermenigvuldiging. Je hebt misschien al de FOIL-methode geleerd, of "Eerst, Buiten, Binnen, Laatste," om uitdrukkingen zoals (x + 2) (x + 4) te vermenigvuldigen. Het is handig om te weten hoe dit werkt voordat we tot factoring komen:  2 Begrijp factoring. Wanneer u twee binomials samen vermenigvuldigt in de FOL-methode, krijgt u een trinominaal (een uitdrukking met drie termen) in de vorm eenX2+bx +c, waar a, b en c gewone nummers zijn. Als je begint met een vergelijking in dezelfde vorm, kun je het terug in twee binomials factoreren.
2 Begrijp factoring. Wanneer u twee binomials samen vermenigvuldigt in de FOL-methode, krijgt u een trinominaal (een uitdrukking met drie termen) in de vorm eenX2+bx +c, waar a, b en c gewone nummers zijn. Als je begint met een vergelijking in dezelfde vorm, kun je het terug in twee binomials factoreren.  3 Schrijf een spatie voor het antwoord in FOIL-vorm. Schrijf voor nu (__ __)(__ __) in de ruimte waar je het antwoord schrijft. We zullen dit invullen als we gaan.
3 Schrijf een spatie voor het antwoord in FOIL-vorm. Schrijf voor nu (__ __)(__ __) in de ruimte waar je het antwoord schrijft. We zullen dit invullen als we gaan. 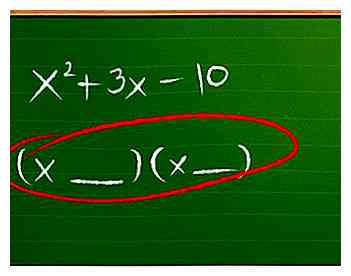 4 Vul de eerste voorwaarden in. Voor eenvoudige problemen, waarbij de eerste term van je trinominaal slechts x is2, de termen in de eerste positie zullen dat altijd zijn X en X. Dit zijn de factoren van de term x2, sinds x keer x = x2.
4 Vul de eerste voorwaarden in. Voor eenvoudige problemen, waarbij de eerste term van je trinominaal slechts x is2, de termen in de eerste positie zullen dat altijd zijn X en X. Dit zijn de factoren van de term x2, sinds x keer x = x2.  5 Gebruik factoring om naar de laatste termen te raden. Als je teruggaat en de stap van de FOIL-methode opnieuw leest, zul je zien dat het vermenigvuldigen van de laatste termen samen de laatste term in de polynoom geeft (de ene zonder x). Dus voor factor, we moeten twee nummers vinden vermenigvuldigen om de laatste term te vormen.
5 Gebruik factoring om naar de laatste termen te raden. Als je teruggaat en de stap van de FOIL-methode opnieuw leest, zul je zien dat het vermenigvuldigen van de laatste termen samen de laatste term in de polynoom geeft (de ene zonder x). Dus voor factor, we moeten twee nummers vinden vermenigvuldigen om de laatste term te vormen.  6 Test welke mogelijkheden werken met vermenigvuldiging van buiten en van binnen. We hebben de laatste termen beperkt tot enkele mogelijkheden. Gebruik vallen en opstaan om elke mogelijkheid te testen, vermenigvuldig de termen Buiten en Binnen en vergelijk het resultaat met onze trinominaal. Bijvoorbeeld:
6 Test welke mogelijkheden werken met vermenigvuldiging van buiten en van binnen. We hebben de laatste termen beperkt tot enkele mogelijkheden. Gebruik vallen en opstaan om elke mogelijkheid te testen, vermenigvuldig de termen Buiten en Binnen en vergelijk het resultaat met onze trinominaal. Bijvoorbeeld: 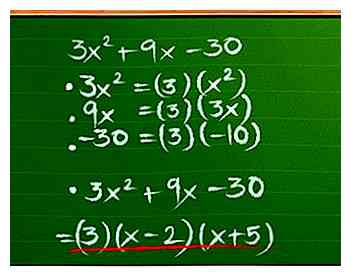 1 Gebruik eenvoudige factoring om gecompliceerdere problemen eenvoudiger te maken. Laten we zeggen dat je moet factor 3x2 + 9x - 30. Zoek naar iets dat bijdraagt aan elk van de drie termen (de "grootste gemene deler" of GCF).[1] In dit geval is het 3:
1 Gebruik eenvoudige factoring om gecompliceerdere problemen eenvoudiger te maken. Laten we zeggen dat je moet factor 3x2 + 9x - 30. Zoek naar iets dat bijdraagt aan elk van de drie termen (de "grootste gemene deler" of GCF).[1] In dit geval is het 3:  2 Zoek naar lastiger factoren. Soms kan de factor variabelen omvatten, of het kan een paar keer nodig zijn om een factor te berekenen om de eenvoudigst mogelijke uitdrukking te vinden. Hier zijn een paar voorbeelden:
2 Zoek naar lastiger factoren. Soms kan de factor variabelen omvatten, of het kan een paar keer nodig zijn om een factor te berekenen om de eenvoudigst mogelijke uitdrukking te vinden. Hier zijn een paar voorbeelden:  3 Los problemen op met een nummer voor de x2. Sommige kwadratische trinomialen kunnen niet worden vereenvoudigd tot het eenvoudigste type probleem. Leer hoe problemen zoals 3x op te lossen2 + 10x + 8, oefen dan alleen, met de voorbeeldproblemen onderaan de pagina:
3 Los problemen op met een nummer voor de x2. Sommige kwadratische trinomialen kunnen niet worden vereenvoudigd tot het eenvoudigste type probleem. Leer hoe problemen zoals 3x op te lossen2 + 10x + 8, oefen dan alleen, met de voorbeeldproblemen onderaan de pagina: 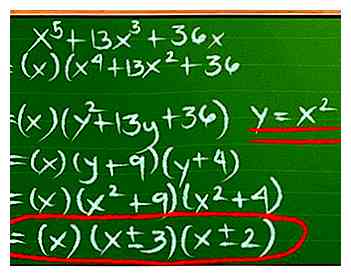 4 Gebruik substitutie voor Trinominals van hogere graden. Je wiskundeboek kan je verrassen met een vergelijking met een hoge exponent, zoals x4, zelfs nadat u eenvoudige factoring hebt gebruikt om het probleem eenvoudiger te maken. Probeer een nieuwe variabele te vervangen die het verandert in een probleem dat u weet op te lossen. Bijvoorbeeld:
4 Gebruik substitutie voor Trinominals van hogere graden. Je wiskundeboek kan je verrassen met een vergelijking met een hoge exponent, zoals x4, zelfs nadat u eenvoudige factoring hebt gebruikt om het probleem eenvoudiger te maken. Probeer een nieuwe variabele te vervangen die het verandert in een probleem dat u weet op te lossen. Bijvoorbeeld:  1 Controleer op priemgetallen. Controleer om te zien of de constante in de eerste of derde termijn van de trinominale een priemgetal is. Een priemgetal kan alleen gelijkmatig alleen worden gedeeld en 1, dus er is slechts één mogelijk paar binomiale factors.br>
1 Controleer op priemgetallen. Controleer om te zien of de constante in de eerste of derde termijn van de trinominale een priemgetal is. Een priemgetal kan alleen gelijkmatig alleen worden gedeeld en 1, dus er is slechts één mogelijk paar binomiale factors.br>  2 Controleer om te zien of de trinominale een perfect vierkant is. Een perfect vierkant trinominaal kan worden verwerkt in twee identieke binomials, en de factor wordt meestal geschreven (x + 1)2 in plaats van (x + 1) (x + 1). Hier een paar veel voorkomende die de neiging hebben om in problemen te verschijnen:
2 Controleer om te zien of de trinominale een perfect vierkant is. Een perfect vierkant trinominaal kan worden verwerkt in twee identieke binomials, en de factor wordt meestal geschreven (x + 1)2 in plaats van (x + 1) (x + 1). Hier een paar veel voorkomende die de neiging hebben om in problemen te verschijnen:  3 Controleer of er geen oplossing bestaat. Niet alle trinomialen kunnen worden verwerkt. Als je vastzit aan een kwadratische drievoudigheid (bijl2+ bx + c), gebruik de kwadratische formule om het antwoord te vinden. Als de enige antwoorden de vierkantswortel van een negatief getal zijn, bestaan er geen echte oplossingen, dus er zijn geen factoren.
3 Controleer of er geen oplossing bestaat. Niet alle trinomialen kunnen worden verwerkt. Als je vastzit aan een kwadratische drievoudigheid (bijl2+ bx + c), gebruik de kwadratische formule om het antwoord te vinden. Als de enige antwoorden de vierkantswortel van een negatief getal zijn, bestaan er geen echte oplossingen, dus er zijn geen factoren.