De Mandelbrot-set bestaat uit punten die op een complex vlak zijn uitgezet om een te vormen fractal: een opvallende vorm of vorm waarin elk deel in feite een miniatuurkopie van het geheel is. De ongelooflijke oogverblindende beelden die in de Mandelbrot-reeks verborgen waren, konden in de 16e eeuw worden bekeken dankzij Rafael Bombelli's begrip van imaginaire getallen - maar pas toen Benoit Mandelbrot en anderen fractalen begonnen te verkennen met behulp van computers, werd het geheime universum onthuld .
Nu we weten dat het bestaat, kunnen we het op een meer primitieve manier benaderen: met de hand. Hier is een methode om een ruwe weergave van de set te bekijken, gewoon om te begrijpen hoe het gedaan is; je krijgt dan een veel diepere waardering voor de renderings die je kunt maken met behulp van de vele open-source computerprogramma's die beschikbaar zijn, of die je kunt bekijken op cd-rom en dvd.
Stappen
-
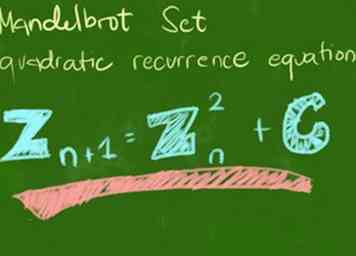 1 Begrijp de basisformule, vaak uitgedrukt als z = z2 + c. Dit betekent eenvoudig dat we voor elk punt in het Mandelbrot-universum dat we willen zien, we blijven rekenen z totdat een van de twee voorwaarden optreedt; dan kleuren we het om te laten zien hoeveel berekeningen we hebben gemaakt. Maak je geen zorgen! Dit wordt duidelijk in de volgende stappen.
1 Begrijp de basisformule, vaak uitgedrukt als z = z2 + c. Dit betekent eenvoudig dat we voor elk punt in het Mandelbrot-universum dat we willen zien, we blijven rekenen z totdat een van de twee voorwaarden optreedt; dan kleuren we het om te laten zien hoeveel berekeningen we hebben gemaakt. Maak je geen zorgen! Dit wordt duidelijk in de volgende stappen. -
 2 Krijg 3 verschillende kleurpotloden, of kleurpotloden, of viltstiften, plus een zwart potlood of pen om de omtrek te maken. De reden dat we drie kleuren willen, is omdat we een eerste benadering maken met niet meer dan 3 iteraties (passen, of met andere woorden, de formule maximaal 3 keer per punt toepassen):
2 Krijg 3 verschillende kleurpotloden, of kleurpotloden, of viltstiften, plus een zwart potlood of pen om de omtrek te maken. De reden dat we drie kleuren willen, is omdat we een eerste benadering maken met niet meer dan 3 iteraties (passen, of met andere woorden, de formule maximaal 3 keer per punt toepassen): -
 3 Teken met de zwarte marker een groot bord met boter en kaas, 3 bij 3 vierkanten, op een vel papier.
3 Teken met de zwarte marker een groot bord met boter en kaas, 3 bij 3 vierkanten, op een vel papier. -
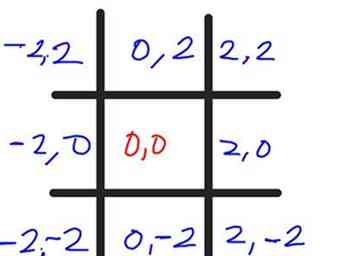 4 Label (ook in het zwart) het middelste vierkant (0, 0). Dit is de constante (c) waarde van het punt in het exacte midden van het vierkant. Laten we nu zeggen dat elk vierkant 2 eenheden breed is, dus optellen en / of 2 aftrekken van / van het X en Y waarden van elk vierkant, met X zijnde het eerste nummer en Y het tweede nummer zijn. Als u klaar bent, ziet het eruit als wat u hier ziet. Telkens wanneer u de cellen volgt, moeten de y-waarden (het tweede getal) hetzelfde zijn; telkens wanneer u de cellen volgt, moeten de x-waarden (het eerste cijfer) hetzelfde zijn.
4 Label (ook in het zwart) het middelste vierkant (0, 0). Dit is de constante (c) waarde van het punt in het exacte midden van het vierkant. Laten we nu zeggen dat elk vierkant 2 eenheden breed is, dus optellen en / of 2 aftrekken van / van het X en Y waarden van elk vierkant, met X zijnde het eerste nummer en Y het tweede nummer zijn. Als u klaar bent, ziet het eruit als wat u hier ziet. Telkens wanneer u de cellen volgt, moeten de y-waarden (het tweede getal) hetzelfde zijn; telkens wanneer u de cellen volgt, moeten de x-waarden (het eerste cijfer) hetzelfde zijn. - 5 Bereken de eerste pas, of herhaling, van de formule. Jij, als de computer (eigenlijk, de oorspronkelijke betekenis van het woord was "een persoon die berekent") kan dit zelf doen. Laten we beginnen met deze veronderstellingen:
- De startwaarde z van elk vierkant is (0, 0). Wanneer de absolute waarde van z voor een bepaald punt groter is dan of gelijk aan 2, wordt gezegd dat dat punt (en het bijbehorende vierkant) ontsnapt de Mandelbrot-set. Wanneer dat gebeurt, kleurt u het vierkant volgens het aantal iteraties van de formule die u op dat punt hebt toegepast.
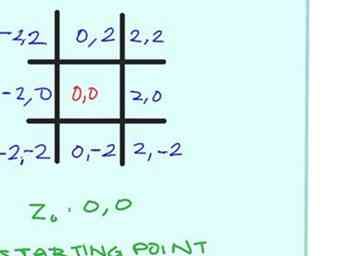
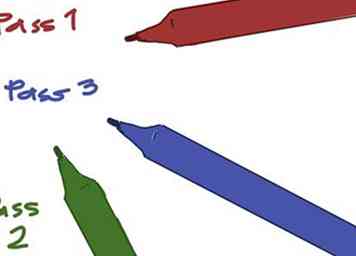
- Kies de kleuren die u wilt gebruiken voor pass 1, pass 2 en pass 3. Laten we aannemen dat rood, groen en blauw, voor de doeleinden van dit artikel.
- Bereken de waarde van z voor de linkerbovenhoek van het tic-tac-toe bord, uitgaande van een startzwaarde van 0 + 0i of (0, 0) (zie Tips voor een beter begrip van deze representaties). We gebruiken de formule z = z2 + c zoals beschreven in de eerste stap. Je zult snel zien dat, in dit geval, z2+ c is eenvoudig c, omdat nulkwadraat nog steeds nul is. En wat is c voor dit plein? (-2, 2).
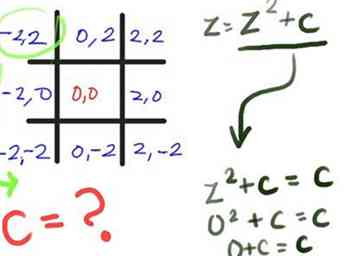
- Bepaal de absolute waarde van dit punt; de absolute waarde van een complex getal (a, b) is de vierkantswortel van a2 + b2. Nu, omdat we dit vergelijken met een bekende waarde: 2, we kunnen voorkomen dat we wortels nemen door a te vergelijken2 + b2 tot 22, waarvan we weten dat het gelijk is 4. In deze berekening, a = -2 en b = 2.

- ([-2]2 + 22) =
- (4 + 4) =
- 8, die groter is dan 4.
- Het is aan de Mandelbrot-set ontsnapt na de eerste berekening, omdat de absolute waarde groter is dan 2. Kleur deze met het potlood dat u hebt gekozen voor pass 1.
-
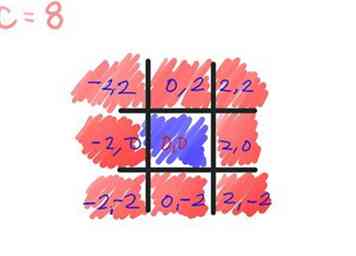
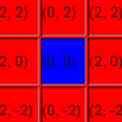 Doe hetzelfde voor elk vakje op het bord, behalve het middenvierkant dat de Mandelbrot bij de 3e pas niet zal verlaten (en nooit zal ontsnappen). U hebt dus maar twee kleuren gebruikt: de kleur voor kleur 1 voor alle buitenste vierkanten en de kleur voor kleur 3 voor het middelste vierkant.
Doe hetzelfde voor elk vakje op het bord, behalve het middenvierkant dat de Mandelbrot bij de 3e pas niet zal verlaten (en nooit zal ontsnappen). U hebt dus maar twee kleuren gebruikt: de kleur voor kleur 1 voor alle buitenste vierkanten en de kleur voor kleur 3 voor het middelste vierkant.
- De startwaarde z van elk vierkant is (0, 0). Wanneer de absolute waarde van z voor een bepaald punt groter is dan of gelijk aan 2, wordt gezegd dat dat punt (en het bijbehorende vierkant) ontsnapt de Mandelbrot-set. Wanneer dat gebeurt, kleurt u het vierkant volgens het aantal iteraties van de formule die u op dat punt hebt toegepast.
-
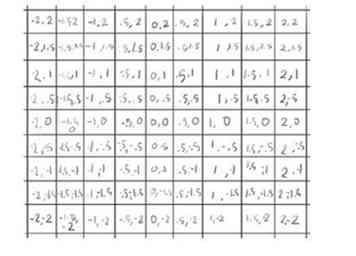 6 Laten we een vierkant 3 keer groter proberen, 9 bij 9, maar nog steeds met een maximum van 3 iteraties.
6 Laten we een vierkant 3 keer groter proberen, 9 bij 9, maar nog steeds met een maximum van 3 iteraties. - 7 Begin met de 3e rij omlaag, want daar wordt het meteen interessant.
- Het eerste element (-2, 1) is groter dan 2 (omdat (-2)2 + 12 blijkt 5) dus laten we die rood schilderen, omdat deze bij de eerste passage de Mandelbrot-set ontwijkt.
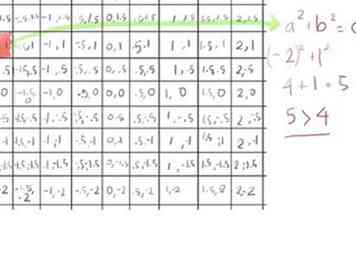
- Het tweede element (-1,5, 1) blijkt niet groter te zijn dan 2. De formule voor absolute waarde toe te passen, x2+ y2, met x = -1,5 en y = 1:
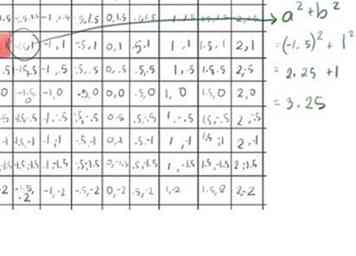
- (-1.5)2 = 2.25
- 12 = 1
- 2,25 + 1 = 3,25, minder dan 4, dus de vierkantswortel is minder dan 2.
- Dus gaan we verder naar onze tweede pass, berekening van z2+ c met behulp van de snelkoppeling (x2-y2, 2xy) voor z2 (zie Tips voor hoe deze snelkoppeling is afgeleid), nog steeds met x = -1,5 en y = 1:
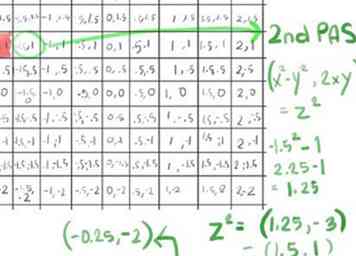
- (-1.5)2 - 12 wordt 2,25 - 1, wat wordt 1.25;
- 2xy, omdat x -1,5 is en y 1 is, wordt 2 (-1,5), wat oplevert -3.0;
- Dit geeft ons een z2 van (1.25, -3)
- Nu toevoegen c voor deze cel (voeg x toe aan x, y aan y) opbrengst (-0,25, -2)
- Laten we testen of de absolute waarde nu groter is dan 2 :. Bereken x2 + y2:
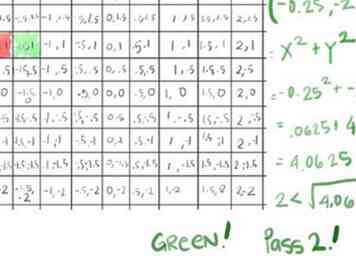
- (-.25)2 = .0625
- -22 = 4
- .0625 + 4 = 4.0625, waarvan de vierkantswortel groter is dan 2, dus is het ontsnapt na de tweede iteratie: onze eerste groen!
- Naarmate je bekend raakt met de berekeningen, kun je soms zien aan welke personen de Mandelbrot-set ontsnapt door alleen maar naar de cijfers te kijken.In dit voorbeeld heeft de y-component een grootte van 2, die in het kwadraat en toegevoegd aan de vierkante waarde van het andere getal groter is dan 4. Elk getal groter dan 4 heeft een vierkantswortel groter dan 2. Zie de Tips hieronder voor een meer gedetailleerde uitleg.
- Het derde element, met een c-waarde van (-1, 1), ontkomt niet aan de eerste passage: aangezien zowel 1 als -1 als vierkant is 1, x2+ y2 is 2. Dus we berekenen z2+ c, met behulp van de snelkoppeling (x2-y2, 2xy) voor z2:

- (-1)2-12 wordt 1-1, wat 0 is;
- 2xy is dan 2 (-1) = -2;
- z2 = (0, -2)
- door c toe te voegen krijgen we (0, -2) + (-1, 1) = (-1, -1)
- Dat is nog steeds dezelfde absolute waarde als voorheen (de vierkantswortel van twee, ongeveer 1,41); doorgaan met een derde iteratie:
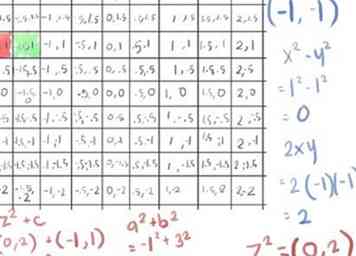
- ([-1]2)-([-1]2) wordt 1-1, wat 0 (alweer) is ...
- maar nu is 2xy 2 (-1) (- 1), wat positief 2 is, wat een z oplevert2 waarde van (0, 2)
- door c toe te voegen krijgen we (0, 2) + (-1, 1) = (-1, 3), die een a heeft2 + b2 van 10, veel groter dan 4.
- Zo ontsnapt ook deze. Kleur de cel in met je derde kleur, blauw en ga verder met de volgende, omdat we met dit punt drie iteraties hebben voltooid.
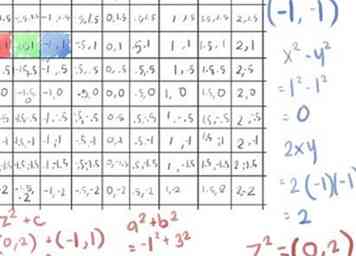
- Het feit dat we slechts drie kleuren gebruiken, wordt hier duidelijk als een probleem, aangezien iets dat na slechts 3 iteraties ontsnapt, hetzelfde kleurt als (0, 0) nooit ontsnapt; uiteraard zullen we nog steeds niets van de "bug" van Mandelbrot op dit detailniveau zien.
- Het eerste element (-2, 1) is groter dan 2 (omdat (-2)2 + 12 blijkt 5) dus laten we die rood schilderen, omdat deze bij de eerste passage de Mandelbrot-set ontwijkt.
-
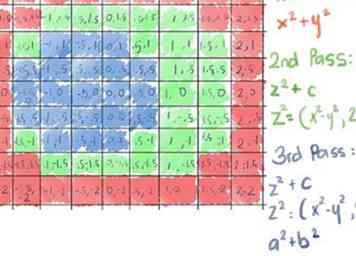 8 Ga door met het berekenen van elke cel totdat het is ontsnapt, of je hebt het maximale aantal iteraties bereikt (het aantal kleuren dat je gebruikt: 3 in dit voorbeeld), op welk punt u het kleurt. Hier ziet u hoe de 9 bij 9 matrix 3 iteraties op elk vierkant controleert ... Lijkt erop dat we iets op het spoor zijn!
8 Ga door met het berekenen van elke cel totdat het is ontsnapt, of je hebt het maximale aantal iteraties bereikt (het aantal kleuren dat je gebruikt: 3 in dit voorbeeld), op welk punt u het kleurt. Hier ziet u hoe de 9 bij 9 matrix 3 iteraties op elk vierkant controleert ... Lijkt erop dat we iets op het spoor zijn! - 9 Herhaal dezelfde matrix opnieuw met meer kleuren (iteraties) om de volgende paar lagen te onthullen, of beter, maak een veel grotere matrix voor een project op langere termijn! Je krijgt meer accurate foto's door:
-
 Het aantal cellen vergroten; dit heeft 81 cellen per zijde. Let op de gelijkenis met de 9 bij 9 matrix hierboven, maar de veel gladdere randen op de cirkel en ovaal.
Het aantal cellen vergroten; dit heeft 81 cellen per zijde. Let op de gelijkenis met de 9 bij 9 matrix hierboven, maar de veel gladdere randen op de cirkel en ovaal. -
 Het aantal kleuren verhogen (iteraties); deze heeft 256 tinten, elk rood, groen en blauw voor een totaal van 768 kleuren in vergelijking met 3. Merk op dat je nu de omtrek van het bekende "meer" van Mandelbrot (of "bug") kunt zien, afhankelijk van hoe je eruit ziet erop). Het nadeel is de hoeveelheid tijd die het kost; als je elke iteratie in 10 seconden kunt berekenen, is dat ongeveer 2 uur voor elke cel in, of in de buurt van, het Mandelbrot-meer. Hoewel dat een relatief klein deel is van de 81 bij 81 matrix, zou het waarschijnlijk nog een jaar duren om het af te maken, zelfs als je er meerdere uren per dag aan hebt gewerkt. Dit is waar de silicium-type computer van pas komt.
Het aantal kleuren verhogen (iteraties); deze heeft 256 tinten, elk rood, groen en blauw voor een totaal van 768 kleuren in vergelijking met 3. Merk op dat je nu de omtrek van het bekende "meer" van Mandelbrot (of "bug") kunt zien, afhankelijk van hoe je eruit ziet erop). Het nadeel is de hoeveelheid tijd die het kost; als je elke iteratie in 10 seconden kunt berekenen, is dat ongeveer 2 uur voor elke cel in, of in de buurt van, het Mandelbrot-meer. Hoewel dat een relatief klein deel is van de 81 bij 81 matrix, zou het waarschijnlijk nog een jaar duren om het af te maken, zelfs als je er meerdere uren per dag aan hebt gewerkt. Dit is waar de silicium-type computer van pas komt.
-
 Minotauromaquia
Minotauromaquia
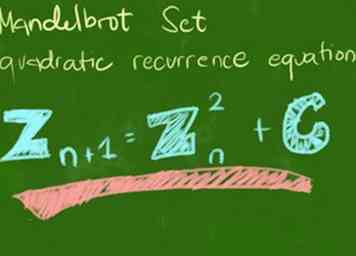 1 Begrijp de basisformule, vaak uitgedrukt als z = z2 + c. Dit betekent eenvoudig dat we voor elk punt in het Mandelbrot-universum dat we willen zien, we blijven rekenen z totdat een van de twee voorwaarden optreedt; dan kleuren we het om te laten zien hoeveel berekeningen we hebben gemaakt. Maak je geen zorgen! Dit wordt duidelijk in de volgende stappen.
1 Begrijp de basisformule, vaak uitgedrukt als z = z2 + c. Dit betekent eenvoudig dat we voor elk punt in het Mandelbrot-universum dat we willen zien, we blijven rekenen z totdat een van de twee voorwaarden optreedt; dan kleuren we het om te laten zien hoeveel berekeningen we hebben gemaakt. Maak je geen zorgen! Dit wordt duidelijk in de volgende stappen.  2 Krijg 3 verschillende kleurpotloden, of kleurpotloden, of viltstiften, plus een zwart potlood of pen om de omtrek te maken. De reden dat we drie kleuren willen, is omdat we een eerste benadering maken met niet meer dan 3 iteraties (passen, of met andere woorden, de formule maximaal 3 keer per punt toepassen):
2 Krijg 3 verschillende kleurpotloden, of kleurpotloden, of viltstiften, plus een zwart potlood of pen om de omtrek te maken. De reden dat we drie kleuren willen, is omdat we een eerste benadering maken met niet meer dan 3 iteraties (passen, of met andere woorden, de formule maximaal 3 keer per punt toepassen):  3 Teken met de zwarte marker een groot bord met boter en kaas, 3 bij 3 vierkanten, op een vel papier.
3 Teken met de zwarte marker een groot bord met boter en kaas, 3 bij 3 vierkanten, op een vel papier.  4 Label (ook in het zwart) het middelste vierkant (0, 0). Dit is de constante (c) waarde van het punt in het exacte midden van het vierkant. Laten we nu zeggen dat elk vierkant 2 eenheden breed is, dus optellen en / of 2 aftrekken van / van het X en Y waarden van elk vierkant, met X zijnde het eerste nummer en Y het tweede nummer zijn. Als u klaar bent, ziet het eruit als wat u hier ziet. Telkens wanneer u de cellen volgt, moeten de y-waarden (het tweede getal) hetzelfde zijn; telkens wanneer u de cellen volgt, moeten de x-waarden (het eerste cijfer) hetzelfde zijn.
4 Label (ook in het zwart) het middelste vierkant (0, 0). Dit is de constante (c) waarde van het punt in het exacte midden van het vierkant. Laten we nu zeggen dat elk vierkant 2 eenheden breed is, dus optellen en / of 2 aftrekken van / van het X en Y waarden van elk vierkant, met X zijnde het eerste nummer en Y het tweede nummer zijn. Als u klaar bent, ziet het eruit als wat u hier ziet. Telkens wanneer u de cellen volgt, moeten de y-waarden (het tweede getal) hetzelfde zijn; telkens wanneer u de cellen volgt, moeten de x-waarden (het eerste cijfer) hetzelfde zijn. 

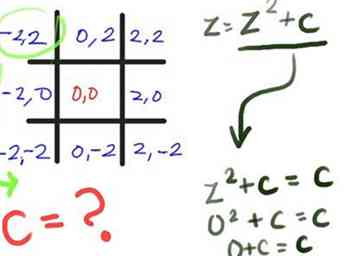


 Doe hetzelfde voor elk vakje op het bord, behalve het middenvierkant dat de Mandelbrot bij de 3e pas niet zal verlaten (en nooit zal ontsnappen). U hebt dus maar twee kleuren gebruikt: de kleur voor kleur 1 voor alle buitenste vierkanten en de kleur voor kleur 3 voor het middelste vierkant.
Doe hetzelfde voor elk vakje op het bord, behalve het middenvierkant dat de Mandelbrot bij de 3e pas niet zal verlaten (en nooit zal ontsnappen). U hebt dus maar twee kleuren gebruikt: de kleur voor kleur 1 voor alle buitenste vierkanten en de kleur voor kleur 3 voor het middelste vierkant. 6 Laten we een vierkant 3 keer groter proberen, 9 bij 9, maar nog steeds met een maximum van 3 iteraties.
6 Laten we een vierkant 3 keer groter proberen, 9 bij 9, maar nog steeds met een maximum van 3 iteraties. 






 8 Ga door met het berekenen van elke cel totdat het is ontsnapt, of je hebt het maximale aantal iteraties bereikt (het aantal kleuren dat je gebruikt: 3 in dit voorbeeld), op welk punt u het kleurt. Hier ziet u hoe de 9 bij 9 matrix 3 iteraties op elk vierkant controleert ... Lijkt erop dat we iets op het spoor zijn!
8 Ga door met het berekenen van elke cel totdat het is ontsnapt, of je hebt het maximale aantal iteraties bereikt (het aantal kleuren dat je gebruikt: 3 in dit voorbeeld), op welk punt u het kleurt. Hier ziet u hoe de 9 bij 9 matrix 3 iteraties op elk vierkant controleert ... Lijkt erop dat we iets op het spoor zijn!  Het aantal cellen vergroten; dit heeft 81 cellen per zijde. Let op de gelijkenis met de 9 bij 9 matrix hierboven, maar de veel gladdere randen op de cirkel en ovaal.
Het aantal cellen vergroten; dit heeft 81 cellen per zijde. Let op de gelijkenis met de 9 bij 9 matrix hierboven, maar de veel gladdere randen op de cirkel en ovaal. Het aantal kleuren verhogen (iteraties); deze heeft 256 tinten, elk rood, groen en blauw voor een totaal van 768 kleuren in vergelijking met 3. Merk op dat je nu de omtrek van het bekende "meer" van Mandelbrot (of "bug") kunt zien, afhankelijk van hoe je eruit ziet erop). Het nadeel is de hoeveelheid tijd die het kost; als je elke iteratie in 10 seconden kunt berekenen, is dat ongeveer 2 uur voor elke cel in, of in de buurt van, het Mandelbrot-meer. Hoewel dat een relatief klein deel is van de 81 bij 81 matrix, zou het waarschijnlijk nog een jaar duren om het af te maken, zelfs als je er meerdere uren per dag aan hebt gewerkt. Dit is waar de silicium-type computer van pas komt.
Het aantal kleuren verhogen (iteraties); deze heeft 256 tinten, elk rood, groen en blauw voor een totaal van 768 kleuren in vergelijking met 3. Merk op dat je nu de omtrek van het bekende "meer" van Mandelbrot (of "bug") kunt zien, afhankelijk van hoe je eruit ziet erop). Het nadeel is de hoeveelheid tijd die het kost; als je elke iteratie in 10 seconden kunt berekenen, is dat ongeveer 2 uur voor elke cel in, of in de buurt van, het Mandelbrot-meer. Hoewel dat een relatief klein deel is van de 81 bij 81 matrix, zou het waarschijnlijk nog een jaar duren om het af te maken, zelfs als je er meerdere uren per dag aan hebt gewerkt. Dit is waar de silicium-type computer van pas komt.