Het bekende rechthoekige raster is een eenvoudig systeem om te leren, maar het is niet in alle situaties handig. Wat als u de spaken op een wiel wilt uitzetten, of de beweging van water in een afvoer? In deze gevallen past een rond coördinatensysteem natuurlijker. In feite heb je het basisidee van poolcoördinaten in het dagelijks leven al gebruikt.[1] Als u bijvoorbeeld de bron van een sirene zoekt, hebt u twee informatie nodig: hoe ver weg het is en in welke richting het geluid komt. Het poolcoördinatenstelsel wijst punten op dezelfde manier toe, waarbij de afstand wordt beschreven vanaf een vast punt en de hoek van een vaste straal.
Deel een van de vier:
Polar-coördinaten uitzetten
-
 1 Stel het poolvlak in. Je hebt waarschijnlijk eerder punten getekend met cartesiaanse coördinaten, met behulp van notatie om locaties op een rechthoekig raster te markeren. Polaire coördinaten gebruiken in plaats daarvan een ander soort grafiek, gebaseerd op cirkels:[2]
1 Stel het poolvlak in. Je hebt waarschijnlijk eerder punten getekend met cartesiaanse coördinaten, met behulp van notatie om locaties op een rechthoekig raster te markeren. Polaire coördinaten gebruiken in plaats daarvan een ander soort grafiek, gebaseerd op cirkels:[2] - Het middelpunt van de grafiek (of "oorsprong" in een rechthoekig raster) is het pool. Je kunt dit labelen met de letter O.
- Begin bij de paal en teken een horizontale lijn naar rechts. Dit is de polaire as. Label de as met eenheden net als de positieve x-as op een rechthoekig raster.
- Als je speciaal polar graph-papier hebt, bevat het veel cirkels van verschillende groottes, allemaal gecentreerd op de paal. U hoeft deze zelf niet te tekenen als u blanco papier gebruikt.
-
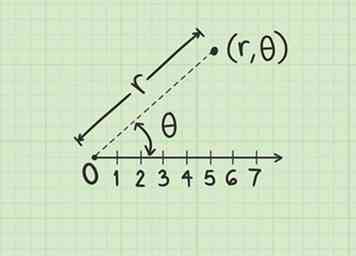 2 Begrijp polaire coördinaten. Op het polaire vlak wordt een punt weergegeven door een coördinaat in de vorm :
2 Begrijp polaire coördinaten. Op het polaire vlak wordt een punt weergegeven door een coördinaat in de vorm : - De eerste variabele, , staat voor radius. Het punt bevindt zich op een cirkel met een straal , gecentreerd op de paal (oorsprong).
- De tweede variabele, , vertegenwoordigt een hoek. Het punt bevindt zich langs een lijn die door de paal loopt en een hoek vormt met de polaire as.
-
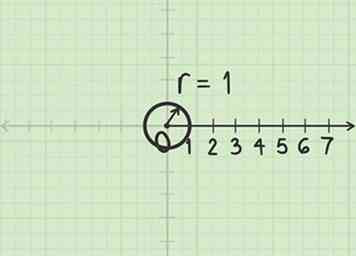 3 Bekijk de eenheidscirkel. In poolcoördinaten wordt de hoek meestal gemeten in radialen in plaats van graden. In dit systeem dekt een volledige rotatie (360º of een volledige cirkel) een hoek van 2 af radialen. (Deze waarde wordt gekozen omdat een cirkel met straal 1 een omtrek van 2 heeft.) Als u uzelf vertrouwd maakt met de eenheidscirkel, wordt het werken met poolcoördinaten veel eenvoudiger.
3 Bekijk de eenheidscirkel. In poolcoördinaten wordt de hoek meestal gemeten in radialen in plaats van graden. In dit systeem dekt een volledige rotatie (360º of een volledige cirkel) een hoek van 2 af radialen. (Deze waarde wordt gekozen omdat een cirkel met straal 1 een omtrek van 2 heeft.) Als u uzelf vertrouwd maakt met de eenheidscirkel, wordt het werken met poolcoördinaten veel eenvoudiger. - Als je leerboek graden gebruikt, hoef je je daar nu geen zorgen over te maken. Het is mogelijk om poolpunten uit te zetten met graden voor .
Deel twee van vier:
Een punt uitzetten
-
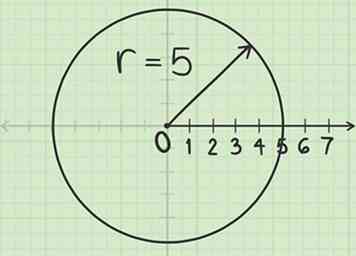 1 Construeer een cirkel met een straal . Enig punt heeft poolcoördinaten in de vorm . Begin met het tekenen van een cirkel met straal , gecentreerd op de paal.
1 Construeer een cirkel met een straal . Enig punt heeft poolcoördinaten in de vorm . Begin met het tekenen van een cirkel met straal , gecentreerd op de paal. - De paal is het middelpunt van de grafiek, waar de oorsprong zich op het rechthoekige coördinatenvlak bevindt.
- Bijvoorbeeld om het punt te plotten , plaats je kompas op de paal. Verleng het potloodeinde van het kompas naar 5 eenheden langs de poolas. Draai het kompas om een cirkel te tekenen.
-
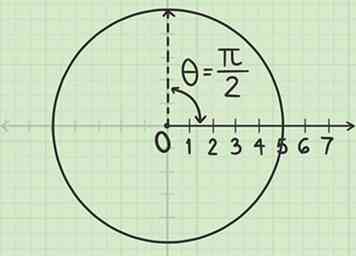 2 Meet een hoek van van de poolas. Plaats een hoekmeter zodat het midden op de paal staat en de rand langs de poolas loopt. Meet de hoek van deze as. Als de hoek in radialen is en uw gradenboog alleen graden aangeeft, kunt u de eenheden omrekenen of naar de eenheidscirkel voor hulp verwijzen.
2 Meet een hoek van van de poolas. Plaats een hoekmeter zodat het midden op de paal staat en de rand langs de poolas loopt. Meet de hoek van deze as. Als de hoek in radialen is en uw gradenboog alleen graden aangeeft, kunt u de eenheden omrekenen of naar de eenheidscirkel voor hulp verwijzen. - Voor het punt , de eenheidscirkel vertelt je dat is ¼ van de manier rond de cirkel, equivalent aan 90 graden van de polaire as.
- Meet altijd positieve hoeken tegen de klok in vanaf de as. Meet negatieve hoeken met de klok mee vanaf de as.
-
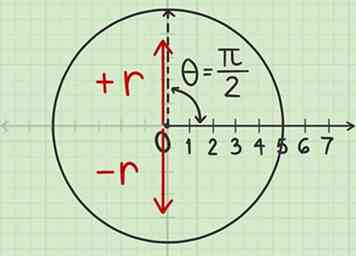 3 Teken een lijn op basis van het teken . De volgende stap is om een lijn te tekenen langs de hoek die je hebt gemeten. Voordat u dit kunt doen, moet u echter weten op welke manier u de grens trekt. Ga terug naar de poolcoördinaten Er achter komen:
3 Teken een lijn op basis van het teken . De volgende stap is om een lijn te tekenen langs de hoek die je hebt gemeten. Voordat u dit kunt doen, moet u echter weten op welke manier u de grens trekt. Ga terug naar de poolcoördinaten Er achter komen: - Als is positief, trek de lijn "vooruit", van de paal recht door de hoekmarkering die u zojuist hebt gemaakt.
- Als is negatief, trek de lijn "achteruit": vanuit de hoekmarkering terug door de paal, om de cirkel aan de andere kant te snijden.
- Wees niet in de war door rechthoekige coördinaten: dit komt niet overeen met positieve of negatieve waarden op een X- of Y- as.
-
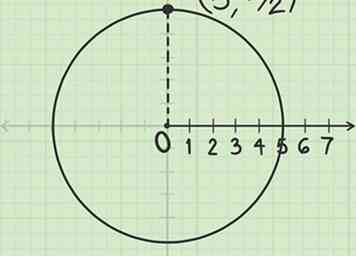 4 Label het punt waar de lijn en cirkel samenkomen. Dit is het punt .
4 Label het punt waar de lijn en cirkel samenkomen. Dit is het punt . - Het punt bevindt zich op een cirkel met straal 5 gecentreerd op de paal, 1/4 van de weg langs de omtrek van de cirkel in een richting tegen de klok in vanaf de polaire as. (Dit punt is equivalent aan (0, 5) in rechthoekige coördinaten.)
Deel drie van vier:
Voorbeelden
Eerste voorbeeld
Zet het punt P uit op op het poolvlak
-
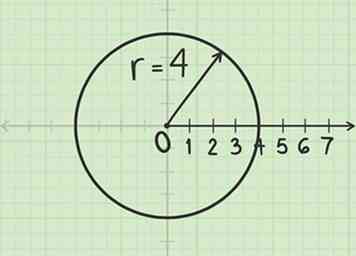 1 Construeer een cirkel met een straal . Gebruik de paal als middelpunt.
1 Construeer een cirkel met een straal . Gebruik de paal als middelpunt. -
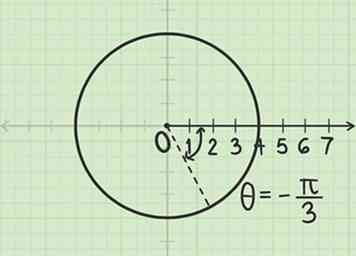 2 Meet de hoek radialen. Meet deze hoek vanaf de polaire as (equivalent aan de positieve x-as). Sinds de hoek is negatief, meet deze hoek met de klok mee.
2 Meet de hoek radialen. Meet deze hoek vanaf de polaire as (equivalent aan de positieve x-as). Sinds de hoek is negatief, meet deze hoek met de klok mee. -
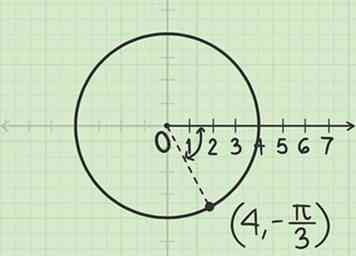 3 Trek een lijn in deze hoek. Begin bij de paal (oorsprong). Aangezien de straal positief is, beweegt u voorwaarts van de pool door de hoek die u hebt gemeten. Het punt waar de lijn de cirkel doorsnijdt is .
3 Trek een lijn in deze hoek. Begin bij de paal (oorsprong). Aangezien de straal positief is, beweegt u voorwaarts van de pool door de hoek die u hebt gemeten. Het punt waar de lijn de cirkel doorsnijdt is .
Tweede voorbeeld
Zet het punt Q uit op op het poolvlak.
-
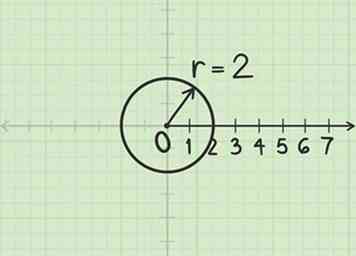 1 Construeer een cirkel met een straal . Gebruik de paal als middelpunt. Hoewel de straal eigenlijk -2 is, is het teken niet belangrijk voor deze stap.
1 Construeer een cirkel met een straal . Gebruik de paal als middelpunt. Hoewel de straal eigenlijk -2 is, is het teken niet belangrijk voor deze stap. -
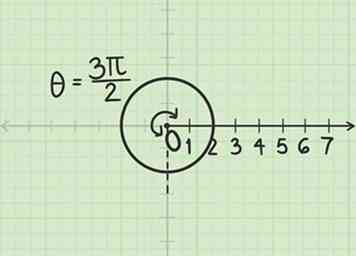 2 Meet de hoek radialen. Sinds de hoek is positief, je moet tegen de klok in van de polaire as.
2 Meet de hoek radialen. Sinds de hoek is positief, je moet tegen de klok in van de polaire as. -
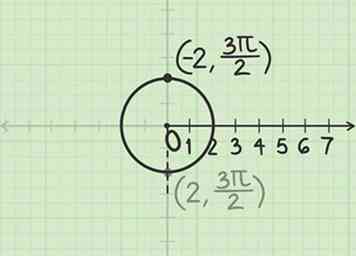 3 Construeer een lijn tegenover die hoek. Sinds de straal is negatief, je moet van de paal in de tegenovergestelde richting van de gegeven hoek gaan. Het punt waar de lijn de cirkel doorsnijdt is .
3 Construeer een lijn tegenover die hoek. Sinds de straal is negatief, je moet van de paal in de tegenovergestelde richting van de gegeven hoek gaan. Het punt waar de lijn de cirkel doorsnijdt is .
Deel vier van vier:
Cartesische coördinaten converteren naar poolcoördinaten
-
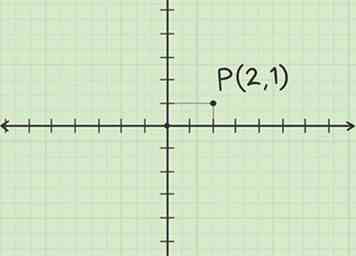 1 Overweeg het punt in het Cartesische vlak. Begin bij de oorsprong en teken een lijnstuk 2 eenheden langs de positieve lijn X-as. Teken een tweede lijnsegment vanaf dat punt 1 eenheid in de positieve richting Y richting. U bevindt zich nu op punt (2, 1), dus label dit punt P.
1 Overweeg het punt in het Cartesische vlak. Begin bij de oorsprong en teken een lijnstuk 2 eenheden langs de positieve lijn X-as. Teken een tweede lijnsegment vanaf dat punt 1 eenheid in de positieve richting Y richting. U bevindt zich nu op punt (2, 1), dus label dit punt P. -
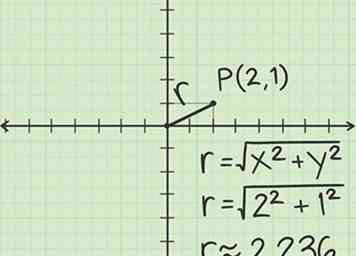 2 Zoek de afstand tussen de oorsprong en . Trek een lijn tussen O en P. Deze lijn heeft lengte in poolcoördinaten. Het is ook de hypotenusa van een rechthoekige driehoek, dus je kunt de lengte van de hypotenusa vinden met behulp van geometrie. Bijvoorbeeld:
2 Zoek de afstand tussen de oorsprong en . Trek een lijn tussen O en P. Deze lijn heeft lengte in poolcoördinaten. Het is ook de hypotenusa van een rechthoekige driehoek, dus je kunt de lengte van de hypotenusa vinden met behulp van geometrie. Bijvoorbeeld: - De poten van deze rechthoekige driehoek hebben waarden van 2 en 1.
- Bereken met de stelling van Pythagoras dat de lengte van de hypotenusa is .
- De algemene formule om te vinden van cartesiaanse coördinaten is , waar is de Cartesiaanse x-coördinaat en de cartesiaanse y-coördinaat.
-
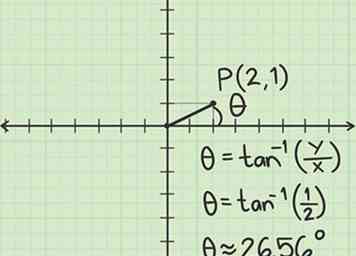 3 Zoek de hoek tussen en de positieve x-as. Gebruik trigonometrie om deze waarde te vinden:
3 Zoek de hoek tussen en de positieve x-as. Gebruik trigonometrie om deze waarde te vinden: -
- De algemene formule om te vinden is , waar is de cartesiaanse y-coördinaat en de cartesiaanse x-coördinaat.
-
-
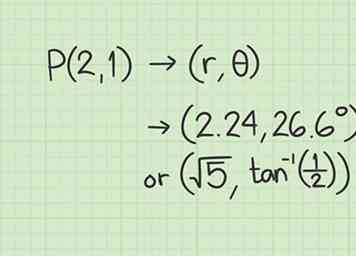 4 Noteer de poolcoördinaten. Je hebt nu de waarden van en . De rechthoekige coördinaten (2, 1) zetten om naar polaire coördinaten van (2.24, 26.6º) of exacte coördinaten van .
4 Noteer de poolcoördinaten. Je hebt nu de waarden van en . De rechthoekige coördinaten (2, 1) zetten om naar polaire coördinaten van (2.24, 26.6º) of exacte coördinaten van .
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Stel het poolvlak in. Je hebt waarschijnlijk eerder punten getekend met cartesiaanse coördinaten, met behulp van
1 Stel het poolvlak in. Je hebt waarschijnlijk eerder punten getekend met cartesiaanse coördinaten, met behulp van  2 Begrijp polaire coördinaten. Op het polaire vlak wordt een punt weergegeven door een coördinaat in de vorm
2 Begrijp polaire coördinaten. Op het polaire vlak wordt een punt weergegeven door een coördinaat in de vorm 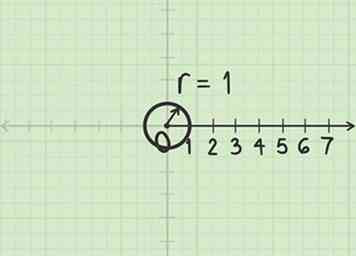 3 Bekijk de eenheidscirkel. In poolcoördinaten wordt de hoek meestal gemeten in radialen in plaats van graden. In dit systeem dekt een volledige rotatie (360º of een volledige cirkel) een hoek van 2 af
3 Bekijk de eenheidscirkel. In poolcoördinaten wordt de hoek meestal gemeten in radialen in plaats van graden. In dit systeem dekt een volledige rotatie (360º of een volledige cirkel) een hoek van 2 af 1 Construeer een cirkel met een straal
1 Construeer een cirkel met een straal  2 Meet een hoek van
2 Meet een hoek van  3 Teken een lijn op basis van het teken
3 Teken een lijn op basis van het teken  4 Label het punt waar de lijn en cirkel samenkomen. Dit is het punt
4 Label het punt waar de lijn en cirkel samenkomen. Dit is het punt  1 Construeer een cirkel met een straal
1 Construeer een cirkel met een straal  2 Meet de hoek
2 Meet de hoek  3 Trek een lijn in deze hoek. Begin bij de paal (oorsprong). Aangezien de straal positief is, beweegt u voorwaarts van de pool door de hoek die u hebt gemeten. Het punt waar de lijn de cirkel doorsnijdt is
3 Trek een lijn in deze hoek. Begin bij de paal (oorsprong). Aangezien de straal positief is, beweegt u voorwaarts van de pool door de hoek die u hebt gemeten. Het punt waar de lijn de cirkel doorsnijdt is  1 Construeer een cirkel met een straal
1 Construeer een cirkel met een straal  2 Meet de hoek
2 Meet de hoek  3 Construeer een lijn tegenover die hoek. Sinds de straal
3 Construeer een lijn tegenover die hoek. Sinds de straal  1 Overweeg het punt
1 Overweeg het punt 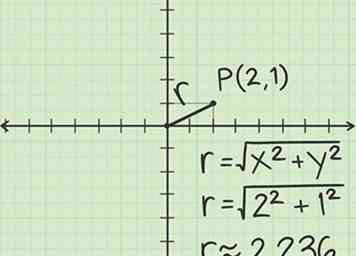 2 Zoek de afstand tussen de oorsprong
2 Zoek de afstand tussen de oorsprong 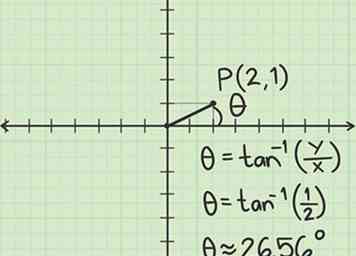 3 Zoek de hoek tussen
3 Zoek de hoek tussen 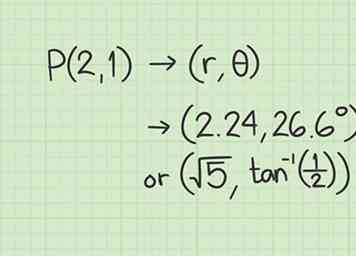 4 Noteer de poolcoördinaten. Je hebt nu de waarden van
4 Noteer de poolcoördinaten. Je hebt nu de waarden van