Het leren van algebra kan intimiderend lijken, maar als je het eenmaal onder de knie hebt, is het niet zo moeilijk! U hoeft alleen maar de volgorde te volgen voor het invullen van delen van de vergelijking en uw werk georganiseerd te houden om fouten te voorkomen!
Deel een van de vijf:
Algemene algebra-regels leren
-
 1 Bekijk je basis wiskundige bewerkingen. Om algebra te leren leren, moet je basisvaardigheden voor wiskunde kennen, zoals optellen, aftrekken, vermenigvuldigen en delen. Deze wiskunde op de basis- / basisschool is essentieel voordat je begint met het leren van de algebra. Als je deze vaardigheden niet beheerst, zal het lastig zijn om de complexere concepten uit de algebra aan te pakken. Als je een opfrissing nodig hebt bij deze operaties, probeer dan ons artikel over elementaire wiskundige vaardigheden.
1 Bekijk je basis wiskundige bewerkingen. Om algebra te leren leren, moet je basisvaardigheden voor wiskunde kennen, zoals optellen, aftrekken, vermenigvuldigen en delen. Deze wiskunde op de basis- / basisschool is essentieel voordat je begint met het leren van de algebra. Als je deze vaardigheden niet beheerst, zal het lastig zijn om de complexere concepten uit de algebra aan te pakken. Als je een opfrissing nodig hebt bij deze operaties, probeer dan ons artikel over elementaire wiskundige vaardigheden. - Dat hoeft niet per se te zijn Super goed bij het doen van deze basishandelingen in je hoofd om algebra-problemen te doen. In veel algebra-klassen kunt u een rekenmachine gebruiken om tijd te besparen bij het uitvoeren van deze eenvoudige handelingen. U moet echter op zijn minst weten hoe u deze bewerkingen moet uitvoeren zonder een rekenmachine voor wanneer u er geen mag gebruiken.
-
 2 Ken de volgorde van operaties. Een van de lastigste dingen over het oplossen van een algebra-vergelijking als beginner is weten waar te beginnen. Gelukkig is er een specifieke volgorde voor het oplossen van deze problemen: doe eerst wiskundige bewerkingen tussen haakjes, dan exponenten, vermenigvuldig dan, deel dan, voeg dan toe en tenslotte af. Een handig hulpmiddel voor het onthouden van deze volgorde van bewerkingen is het acroniem PEMDAS. Leer hier hoe u de volgorde van bewerkingen kunt toepassen. Om samen te vatten, is de volgorde van bewerkingen:
2 Ken de volgorde van operaties. Een van de lastigste dingen over het oplossen van een algebra-vergelijking als beginner is weten waar te beginnen. Gelukkig is er een specifieke volgorde voor het oplossen van deze problemen: doe eerst wiskundige bewerkingen tussen haakjes, dan exponenten, vermenigvuldig dan, deel dan, voeg dan toe en tenslotte af. Een handig hulpmiddel voor het onthouden van deze volgorde van bewerkingen is het acroniem PEMDAS. Leer hier hoe u de volgorde van bewerkingen kunt toepassen. Om samen te vatten, is de volgorde van bewerkingen: - Parentheses
- Exponents
- Multiplication
- DiVision
- EENddition
- Subtraction
- De volgorde van bewerkingen is belangrijk in de algebra omdat het uitvoeren van de bewerkingen in een algebra probleem in de verkeerde volgorde soms het antwoord kan beïnvloeden. Als we bijvoorbeeld te maken hebben met het wiskundeprobleem 8 + 2 × 5, als we eerst 2 tot 8 optellen, krijgen we 10 × 5 = 50, maar als we eerst 2 en 5 vermenigvuldigen, krijgen we 8 + 10 = 18. Alleen het tweede antwoord is correct.
-
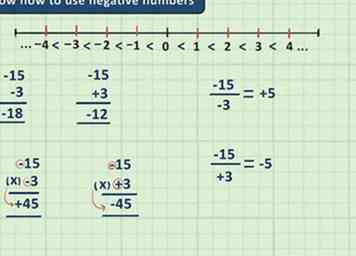 3 Weet hoe je negatieve getallen moet gebruiken. In algebra is het gebruikelijk om negatieve getallen te gebruiken, dus het is slim om te bekijken hoe je negatieven optelt, aftrekt, vermenigvuldigt en deelt voordat je begint met het leren van algebra. Hieronder staan slechts enkele basisprincipes met negatieve getallen om in gedachten te houden. Zie voor meer informatie onze artikelen over het toevoegen en aftrekken van negatieve getallen en het delen en vermenigvuldigen van negatieve getallen.
3 Weet hoe je negatieve getallen moet gebruiken. In algebra is het gebruikelijk om negatieve getallen te gebruiken, dus het is slim om te bekijken hoe je negatieven optelt, aftrekt, vermenigvuldigt en deelt voordat je begint met het leren van algebra. Hieronder staan slechts enkele basisprincipes met negatieve getallen om in gedachten te houden. Zie voor meer informatie onze artikelen over het toevoegen en aftrekken van negatieve getallen en het delen en vermenigvuldigen van negatieve getallen. - Op een getallenlijn staat een negatieve versie van een getal op dezelfde afstand van nul als de positieve, maar in de tegenovergestelde richting.
- Het samenvoegen van twee negatieve getallen maakt het nummer meer negatief (met andere woorden, de cijfers zullen hoger zijn, maar aangezien het aantal negatief is, telt het als zijnde lager)
- Twee negatieve tekens worden geannuleerd - het aftrekken van een negatief getal is hetzelfde als het toevoegen van een positief getal
- Het vermenigvuldigen of delen van twee negatieve getallen geeft een positief antwoord.
- Het vermenigvuldigen of delen van een positief getal en een negatief getal geeft een negatief antwoord.
-
 4 Weet hoe je lange problemen georganiseerd kunt houden. Hoewel eenvoudige algebra problemen een fluitje van een cent kunnen zijn om op te lossen, kunnen meer gecompliceerde problemen vele, vele stappen vereisen. Om fouten te voorkomen, moet u uw werk georganiseerd houden door een nieuwe regel te beginnen elke keer dat u een stap zet in de richting van het oplossen van uw probleem. Als je te maken hebt met een tweezijdige vergelijking, probeer dan alle gelijktekens ("=" s) onder elkaar te schrijven. Op deze manier, als je ergens een fout maakt, zal het veel gemakkelijker te vinden en corrigeren zijn.
4 Weet hoe je lange problemen georganiseerd kunt houden. Hoewel eenvoudige algebra problemen een fluitje van een cent kunnen zijn om op te lossen, kunnen meer gecompliceerde problemen vele, vele stappen vereisen. Om fouten te voorkomen, moet u uw werk georganiseerd houden door een nieuwe regel te beginnen elke keer dat u een stap zet in de richting van het oplossen van uw probleem. Als je te maken hebt met een tweezijdige vergelijking, probeer dan alle gelijktekens ("=" s) onder elkaar te schrijven. Op deze manier, als je ergens een fout maakt, zal het veel gemakkelijker te vinden en corrigeren zijn. - Om bijvoorbeeld de vergelijking 9/3 - 5 + 3 × 4 op te lossen, kunnen we ons probleem als volgt georganiseerd houden:
-
- 9/3 - 5 + 3 × 4
- 9/3 - 5 + 12
- 3 - 5 + 12
- 3 + 7
- 10
-
- Om bijvoorbeeld de vergelijking 9/3 - 5 + 3 × 4 op te lossen, kunnen we ons probleem als volgt georganiseerd houden:
Deel twee van vijf:
Variabelen begrijpen
-
 1 Zoek naar symbolen die geen nummers zijn. In de algebra zie je letters en symbolen verschijnen in je wiskundige problemen, in plaats van alleen cijfers. Dit worden variabelen genoemd. Variabelen zijn niet zo verwarrend als ze misschien lijken - het zijn gewoon manieren om getallen met onbekende waarden te tonen. Hieronder staan slechts enkele algemene voorbeelden van variabelen in de algebra:
1 Zoek naar symbolen die geen nummers zijn. In de algebra zie je letters en symbolen verschijnen in je wiskundige problemen, in plaats van alleen cijfers. Dit worden variabelen genoemd. Variabelen zijn niet zo verwarrend als ze misschien lijken - het zijn gewoon manieren om getallen met onbekende waarden te tonen. Hieronder staan slechts enkele algemene voorbeelden van variabelen in de algebra: - Letters zoals x, y, z, a, b en c
- Griekse letters zoals theta of θ
- Merk op dat niet alle symbolen zijn onbekende variabelen. Bijvoorbeeld, pi, of π, is altijd gelijk aan ongeveer 3.14159.
-
 2 Beschouw variabelen als "onbekende" getallen. Zoals hierboven vermeld, zijn variabelen in feite gewoon cijfers met onbekende waarden. Met andere woorden, er is een nummer dat kan in de plaats van de variabele gaan om de vergelijking te laten werken. Meestal is je doel in een algebra-probleem om erachter te komen wat de variabele is - denk eraan als een "mysterienummer" dat je probeert te ontdekken.
2 Beschouw variabelen als "onbekende" getallen. Zoals hierboven vermeld, zijn variabelen in feite gewoon cijfers met onbekende waarden. Met andere woorden, er is een nummer dat kan in de plaats van de variabele gaan om de vergelijking te laten werken. Meestal is je doel in een algebra-probleem om erachter te komen wat de variabele is - denk eraan als een "mysterienummer" dat je probeert te ontdekken. - Bijvoorbeeld, in de vergelijking 2x + 3 = 11 is x onze variabele. Dit betekent dat er een waarde is die op de plaats van x staat om de linkerkant van de vergelijking gelijk te maken aan 11. Aangezien 2 × 4 + 3 = 11, in dit geval, x = 4.
- Een gemakkelijke manier om variabelen te begrijpen is om ze te vervangen door vraagtekens in algebra-problemen. We zouden bijvoorbeeld de vergelijking 2 + 3 + x = 9 opnieuw kunnen schrijven als 2 + 3 + ? = 9. Dit maakt het makkelijker om te begrijpen wat we proberen te doen - we moeten alleen uitvinden welk nummer we moeten toevoegen aan 2 + 3 = 5 om 9 te krijgen. Het antwoord is opnieuw 4, natuurlijk.
-
 3 Let op terugkerende variabelen. Als een variabele meer dan eens verschijnt, vereenvoudig dan de variabelen. Wat doe je als dezelfde variabele meer dan eens voorkomt in de vergelijking? Hoewel deze situatie lastig lijkt om op te lossen, kunt u variabelen eigenlijk behandelen hoe u normale getallen behandelt. Met andere woorden, u kunt ze toevoegen, aftrekken, enzovoort, zolang u alleen variabelen combineert die op elkaar lijken. Met andere woorden, x + x = 2x, maar x + y is niet gelijk aan 2xy.
3 Let op terugkerende variabelen. Als een variabele meer dan eens verschijnt, vereenvoudig dan de variabelen. Wat doe je als dezelfde variabele meer dan eens voorkomt in de vergelijking? Hoewel deze situatie lastig lijkt om op te lossen, kunt u variabelen eigenlijk behandelen hoe u normale getallen behandelt. Met andere woorden, u kunt ze toevoegen, aftrekken, enzovoort, zolang u alleen variabelen combineert die op elkaar lijken. Met andere woorden, x + x = 2x, maar x + y is niet gelijk aan 2xy. - Laten we bijvoorbeeld de vergelijking 2x + 1x = 9 bekijken. In dit geval kunnen we 2x en 1x samen optellen om 3x = 9 te krijgen. Sinds 3 x 3 = 9 weten we dat x = 3.
- Merk nogmaals op dat u dezelfde variabelen alleen samen kunt toevoegen. In de vergelijking 2x + 1y = 9 kunnen we 2x en 1y niet combineren omdat het twee verschillende variabelen zijn.
- Dit geldt ook wanneer de ene variabele een andere exponent heeft dan de andere. Bijvoorbeeld in de vergelijking 2x + 3x2 = 10, we kunnen 2x en 3x niet combineren2 omdat de x-variabelen verschillende exponenten hebben. Zie Exponenten toevoegen voor meer informatie.
Deel drie van vijf:
Vergelijkingen leren op te lossen door "Annuleren"
-
 1 Probeer de variabele alleen in algebra-vergelijkingen te krijgen. Het oplossen van een vergelijking in de algebra betekent meestal dat je moet uitvinden wat de variabele is. Algebra-vergelijkingen worden meestal ingesteld met cijfers en / of variabelen aan beide zijden, zoals deze: x + 2 = 9 × 4. Om erachter te komen wat de variabele is, moet u hem alleen aan de ene kant van het gelijkteken krijgen. Wat er nog over is aan de andere kant van het gelijkteken is jouw antwoord.
1 Probeer de variabele alleen in algebra-vergelijkingen te krijgen. Het oplossen van een vergelijking in de algebra betekent meestal dat je moet uitvinden wat de variabele is. Algebra-vergelijkingen worden meestal ingesteld met cijfers en / of variabelen aan beide zijden, zoals deze: x + 2 = 9 × 4. Om erachter te komen wat de variabele is, moet u hem alleen aan de ene kant van het gelijkteken krijgen. Wat er nog over is aan de andere kant van het gelijkteken is jouw antwoord. - In het voorbeeld (x + 2 = 9 × 4), om x aan de linkerkant van de vergelijking zelf te krijgen, moeten we de "+ 2" verwijderen. Om dit te doen, zullen we eenvoudig 2 van die kant aftrekken, waardoor we x = 9 × 4 blijven. Om echter beide zijden van de vergelijking gelijk te houden, moeten we ook 2 van de andere kant aftrekken. Dit laat ons achter met x = 9 × 4 - 2. Volgend op de volgorde van bewerkingen, vermenigvuldigen we eerst, trekken we af en geven ons een antwoord van x = 36 - 2 = 34.
-
 2 Annuleer toevoeging met aftrekken (en omgekeerd). Zoals we zojuist hierboven zagen, betekent het feit dat x alleen aan de ene kant van het gelijkteken staat, dat je de getallen ernaast weggooit. Om dit te doen, voeren we de "tegenovergestelde" bewerking uit aan beide zijden van de vergelijking. Bijvoorbeeld, in de vergelijking x + 3 = 0, omdat we een "+ 3" naast onze x zien, zullen we aan beide kanten een "- 3" plaatsen. De "+ 3" en "- 3", waarbij x zichzelf en "-3" aan de andere kant van het gelijkteken verlaten, zoals deze: x = -3.
2 Annuleer toevoeging met aftrekken (en omgekeerd). Zoals we zojuist hierboven zagen, betekent het feit dat x alleen aan de ene kant van het gelijkteken staat, dat je de getallen ernaast weggooit. Om dit te doen, voeren we de "tegenovergestelde" bewerking uit aan beide zijden van de vergelijking. Bijvoorbeeld, in de vergelijking x + 3 = 0, omdat we een "+ 3" naast onze x zien, zullen we aan beide kanten een "- 3" plaatsen. De "+ 3" en "- 3", waarbij x zichzelf en "-3" aan de andere kant van het gelijkteken verlaten, zoals deze: x = -3. - In het algemeen zijn optellen en aftrekken als "tegenstellingen" - doe er een om van de ander af te komen. Zie hieronder:
-
- Voeg voor optellen af. Voorbeeld: x + 9 = 3 → x = 3 - 9
- Voor aftrekken, toevoegen. Voorbeeld: x - 4 = 20 → x = 20 + 4
-
- In het algemeen zijn optellen en aftrekken als "tegenstellingen" - doe er een om van de ander af te komen. Zie hieronder:
-
 3 Annuleer vermenigvuldiging met delen (en omgekeerd). Vermenigvuldigen en delen zijn een beetje moeilijker om mee te werken dan optellen en aftrekken, maar ze hebben dezelfde "tegenovergestelde" relatie. Als u een "× 3" aan één kant ziet, annuleert u deze door beide zijden te delen door 3, enzovoort.
3 Annuleer vermenigvuldiging met delen (en omgekeerd). Vermenigvuldigen en delen zijn een beetje moeilijker om mee te werken dan optellen en aftrekken, maar ze hebben dezelfde "tegenovergestelde" relatie. Als u een "× 3" aan één kant ziet, annuleert u deze door beide zijden te delen door 3, enzovoort. - Met vermenigvuldiging en deling moet u de tegenovergestelde bewerking uitvoeren alles aan de andere kant van het gelijkteken, zelfs als het meer dan één cijfer is. Zie hieronder:
-
- Voor vermenigvuldigen, delen. Voorbeeld: 6x = 14 + 2 → x = (14 + 2)/6
- Voor verdeling, vermenigvuldig. Voorbeeld: x / 5 = 25 → x = 25 × 5
-
- Met vermenigvuldiging en deling moet u de tegenovergestelde bewerking uitvoeren alles aan de andere kant van het gelijkteken, zelfs als het meer dan één cijfer is. Zie hieronder:
-
 4 Annuleer exponenten door de root te nemen (en omgekeerd). Exponenten zijn een vrij uitgebreid pre-algebra-onderwerp - als je niet weet hoe je dit moet doen, bekijk je ons basis exponentartikel voor meer informatie. Het "tegenovergestelde" van een exponent is de wortel die hetzelfde nummer heeft. Bijvoorbeeld het tegenovergestelde van de 2 exponent is een vierkantswortel (√), het tegenovergestelde van de 3 exponent is de kubuswortel (3√), enzovoort.
4 Annuleer exponenten door de root te nemen (en omgekeerd). Exponenten zijn een vrij uitgebreid pre-algebra-onderwerp - als je niet weet hoe je dit moet doen, bekijk je ons basis exponentartikel voor meer informatie. Het "tegenovergestelde" van een exponent is de wortel die hetzelfde nummer heeft. Bijvoorbeeld het tegenovergestelde van de 2 exponent is een vierkantswortel (√), het tegenovergestelde van de 3 exponent is de kubuswortel (3√), enzovoort. - Het is misschien een beetje verwarrend, maar in deze gevallen neem je de wortel van beide kanten wanneer je met een exponent te maken hebt. Aan de andere kant neem je de exponent van beide kanten wanneer je te maken hebt met een root. Zie hieronder:
-
- Neem voor exponenten de root. Voorbeeld: x2 = 49 → x = √49
- Neem voor wortels de exponent. Voorbeeld: √x = 12 → x = 122
-
- Het is misschien een beetje verwarrend, maar in deze gevallen neem je de wortel van beide kanten wanneer je met een exponent te maken hebt. Aan de andere kant neem je de exponent van beide kanten wanneer je te maken hebt met een root. Zie hieronder:
Deel vier van vijf:
Je algebra-vaardigheden verscherpen
-
 1 Gebruik foto's om problemen duidelijker te maken. Als je het moeilijk hebt om een algebra-probleem te visualiseren, probeer dan diagrammen of afbeeldingen te gebruiken om je vergelijking te illustreren. Je kunt zelfs proberen om een groep fysieke objecten (zoals blokken of munten) te gebruiken als je wat handig hebt.
1 Gebruik foto's om problemen duidelijker te maken. Als je het moeilijk hebt om een algebra-probleem te visualiseren, probeer dan diagrammen of afbeeldingen te gebruiken om je vergelijking te illustreren. Je kunt zelfs proberen om een groep fysieke objecten (zoals blokken of munten) te gebruiken als je wat handig hebt. - Laten we bijvoorbeeld de vergelijking x + 2 = 3 oplossen met behulp van kaders (☐)
-
- x +2 = 3
- ☒+☐☐ =☐☐☐
- Op dit punt trekken we 2 van beide kanten af door eenvoudig twee vakken (☐☐) aan beide zijden te verwijderen:
- ☒+☐☐-☐☐ =☐☐☐-☐☐
- ☒ = ☐, of x = 1
-
- Als een ander voorbeeld, laten we 2x = 4 proberen
-
- ☒☒ =☐☐☐☐
- Op dit punt delen we beide zijden door twee door de vakken aan elke kant in twee groepen te scheiden:
- ☒|☒ =☐☐|☐☐
- ☒ = ☐☐, of x = 2
-
- Laten we bijvoorbeeld de vergelijking x + 2 = 3 oplossen met behulp van kaders (☐)
-
 2 Gebruik "gezond verstand" (vooral voor woordproblemen). Wanneer u een woordprobleem in algebra converteert, probeert u uw formule te controleren door eenvoudige waarden voor uw variabele in te voegen. Heeft uw vergelijking zin als x = 0? Wanneer x = 1? Wanneer x = -1? Het is gemakkelijk om eenvoudige fouten te maken door p = 6d op te schrijven als je p = d / 6 bedoelt, maar deze worden gemakkelijk gepakt als je een snelle sanitaire controle op je werk uitvoert voordat je verder gaat.
2 Gebruik "gezond verstand" (vooral voor woordproblemen). Wanneer u een woordprobleem in algebra converteert, probeert u uw formule te controleren door eenvoudige waarden voor uw variabele in te voegen. Heeft uw vergelijking zin als x = 0? Wanneer x = 1? Wanneer x = -1? Het is gemakkelijk om eenvoudige fouten te maken door p = 6d op te schrijven als je p = d / 6 bedoelt, maar deze worden gemakkelijk gepakt als je een snelle sanitaire controle op je werk uitvoert voordat je verder gaat. - Laten we bijvoorbeeld zeggen dat ons wordt verteld dat een voetbalveld 30 yards (27,4 m) langer is dan breed. We gebruiken de vergelijking l = w + 30 om dit weer te geven. We kunnen testen of deze vergelijking zinvol is door eenvoudige waarden voor w in te pluggen. Als het veld bijvoorbeeld w = 10 yards (9,1 m) breed is, is het 10 + 30 = 40 yards (36,6 m) lang. Als het 30 yards (27,4 m) breed is, is het 30 + 30 = 60 yards (54,9 m) lang, enzovoort. Dit is logisch - we verwachten dat het veld langer wordt naarmate het breder wordt, dus deze vergelijking is redelijk.
-
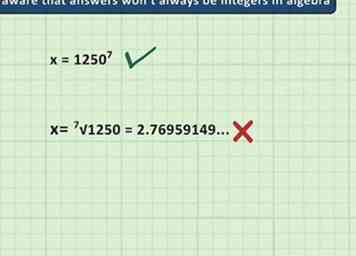 3 Houd er rekening mee dat antwoorden niet altijd gehele getallen in de algebra zijn. Antwoorden in algebra en andere geavanceerde vormen van wiskunde zijn niet altijd ronde, gemakkelijke getallen. Ze kunnen vaak decimalen, breuken of irrationele getallen zijn. Een rekenmachine kan je helpen deze gecompliceerde antwoorden te vinden, maar houd er rekening mee dat je leraar je misschien vraagt om je antwoord in de exacte vorm te geven, niet in een log decimaal.
3 Houd er rekening mee dat antwoorden niet altijd gehele getallen in de algebra zijn. Antwoorden in algebra en andere geavanceerde vormen van wiskunde zijn niet altijd ronde, gemakkelijke getallen. Ze kunnen vaak decimalen, breuken of irrationele getallen zijn. Een rekenmachine kan je helpen deze gecompliceerde antwoorden te vinden, maar houd er rekening mee dat je leraar je misschien vraagt om je antwoord in de exacte vorm te geven, niet in een log decimaal. - Laten we zeggen dat we een algebra-vergelijking beperken tot x = 12507. Als we 1250 typen7 in een rekenmachine krijgen we een enorme reeks decimalen (plus, omdat het scherm van de rekenmachine alleen zo groot is, kan het het hele antwoord niet weergeven.) In dit geval willen we ons antwoord misschien als eenvoudig 1250 voorstellen.7 of anders vereenvoudig het antwoord door het in wetenschappelijke notatie te schrijven.
-
 4 Probeer je vaardigheden uit te breiden. Als je zeker bent van elementaire algebra, probeer dan factoring. Een van de lastigste algebravaardigheden van allemaal is factoring - een soort snelkoppeling voor het verkrijgen van complexe vergelijkingen in eenvoudige vormen. Factoring is een semi-geavanceerd algebra-onderwerp. Overweeg daarom het bovenstaande artikel te raadplegen als u problemen ondervindt om het te beheersen. Hieronder staan slechts een paar snelle tips voor factoring-vergelijkingen:
4 Probeer je vaardigheden uit te breiden. Als je zeker bent van elementaire algebra, probeer dan factoring. Een van de lastigste algebravaardigheden van allemaal is factoring - een soort snelkoppeling voor het verkrijgen van complexe vergelijkingen in eenvoudige vormen. Factoring is een semi-geavanceerd algebra-onderwerp. Overweeg daarom het bovenstaande artikel te raadplegen als u problemen ondervindt om het te beheersen. Hieronder staan slechts een paar snelle tips voor factoring-vergelijkingen: - Vergelijkingen met de vorm ax + ba factor naar a (x + b). Voorbeeld: 2x + 4 = 2 (x + 2)
- Vergelijkingen met de formulierbijl2 + bx factor naar cx ((a / c) x + (b / c)) waarbij c het grootste getal is dat gelijk verdeelt in a en b. Voorbeeld: 3j2 + 12y = 3y (y + 4)
- Vergelijkingen met de vorm x2 + bx + c factor tot (x + y) (x + z) waarbij y × z = c en yx + zx = bx. Voorbeeld: x2 + 4x + 3 = (x + 3) (x + 1).
-
 5 Oefenen, oefenen, oefenen! Vooruitgang in de algebra (en elke andere vorm van wiskunde) vereist veel hard werk en herhaling. Maak je geen zorgen - door al je opdrachten in de klas te volgen en hulp te zoeken van je leraar of andere studenten wanneer je het nodig hebt, zal de algebra een tweede natuur worden.
5 Oefenen, oefenen, oefenen! Vooruitgang in de algebra (en elke andere vorm van wiskunde) vereist veel hard werk en herhaling. Maak je geen zorgen - door al je opdrachten in de klas te volgen en hulp te zoeken van je leraar of andere studenten wanneer je het nodig hebt, zal de algebra een tweede natuur worden. -
 6 Vraag je leraar om je te helpen bij het begrijpen van lastige algebra-onderwerpen. Als je het moeilijk hebt om algebra onder de knie te krijgen, maak je geen zorgen - je hoeft het niet alleen te leren. Je leraar is de eerste persoon waar je terecht moet met vragen. Vraag na de les je leraar vriendelijk om hulp. Goede leraren zijn meestal bereid om het onderwerp van de dag opnieuw uit te leggen op een afspraak na de school en kunnen je misschien zelfs extra oefenmateriaal geven.
6 Vraag je leraar om je te helpen bij het begrijpen van lastige algebra-onderwerpen. Als je het moeilijk hebt om algebra onder de knie te krijgen, maak je geen zorgen - je hoeft het niet alleen te leren. Je leraar is de eerste persoon waar je terecht moet met vragen. Vraag na de les je leraar vriendelijk om hulp. Goede leraren zijn meestal bereid om het onderwerp van de dag opnieuw uit te leggen op een afspraak na de school en kunnen je misschien zelfs extra oefenmateriaal geven. - Als je docent je om wat voor reden dan ook niet kan helpen, probeer hem dan te vragen naar tutoringsopties op jouw school. Veel scholen hebben een soort naschools programma dat je kan helpen extra tijd en aandacht te krijgen die je nodig hebt om te beginnen uit te blinken in je algebra. Vergeet niet dat het gebruik van gratis hulp die voor u beschikbaar is, niet iets is om u voor te schamen - het is een teken dat u slim genoeg bent om uw probleem op te lossen!
Deel Vijf van Vijf:
Intermediaire onderwerpen verkennen
-
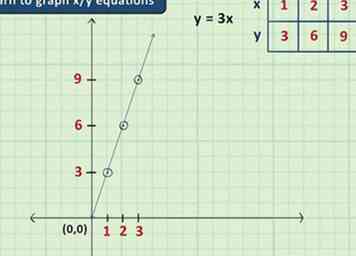 1 Leer x / y-vergelijkingen te maken. Grafieken kunnen waardevolle hulpmiddelen in de algebra zijn, omdat ze u in staat stellen ideeën weer te geven waarvoor u normaal gesproken getallen nodig heeft in gemakkelijk te begrijpen afbeeldingen. Gewoonlijk zijn grafische problemen in de beginalgebra beperkt tot vergelijkingen met twee variabelen (meestal x en y) en worden ze uitgevoerd op een eenvoudige 2-D grafiek met een x-as en een y-as. Met deze vergelijkingen hoeft u alleen maar een waarde in te voeren voor x en vervolgens op te lossen voor y (of omgekeerd) om twee getallen te krijgen die overeenkomen met een punt in de grafiek.
1 Leer x / y-vergelijkingen te maken. Grafieken kunnen waardevolle hulpmiddelen in de algebra zijn, omdat ze u in staat stellen ideeën weer te geven waarvoor u normaal gesproken getallen nodig heeft in gemakkelijk te begrijpen afbeeldingen. Gewoonlijk zijn grafische problemen in de beginalgebra beperkt tot vergelijkingen met twee variabelen (meestal x en y) en worden ze uitgevoerd op een eenvoudige 2-D grafiek met een x-as en een y-as. Met deze vergelijkingen hoeft u alleen maar een waarde in te voeren voor x en vervolgens op te lossen voor y (of omgekeerd) om twee getallen te krijgen die overeenkomen met een punt in de grafiek. - Bijvoorbeeld, in de vergelijking y = 3x, als we 2 voor x inpluggen, krijgen we y = 6. Dit betekent dat het punt (2,6) (twee spaties rechts van het midden en zes spaties boven het midden) maakt deel uit van de grafiek van deze vergelijking.
- Vergelijkingen met de vorm y = mx + b (waarbij m en b getallen zijn) vooral gebruikelijk in elementaire algebra. Deze vergelijkingen hebben altijd een helling van m en kruisen de y-as bij y = b.
-
 2 Leer ongelijkheden op te lossen. Wat doe je als je vergelijking geen gelijkteken gebruikt? Niets anders dan wat je normaal zou doen, blijkt. Voor ongelijkheden, die tekens gebruiken als> ("groter dan") en <("minder dan"), lost u gewoon op zoals normaal. Je blijft zitten met een antwoord dat kleiner of groter is dan je variabele.
2 Leer ongelijkheden op te lossen. Wat doe je als je vergelijking geen gelijkteken gebruikt? Niets anders dan wat je normaal zou doen, blijkt. Voor ongelijkheden, die tekens gebruiken als> ("groter dan") en <("minder dan"), lost u gewoon op zoals normaal. Je blijft zitten met een antwoord dat kleiner of groter is dan je variabele. - Met de vergelijking 3> 5x - 2 zouden we bijvoorbeeld oplossen zoals we zouden doen voor een normale vergelijking:
-
- 3> 5x - 2
- 5> 5x
- 1> x, of x <1.
-
- Dit betekent dat elk nummer minder dan één werkt voor x. Met andere woorden, x kan 0, -1, -2, enzovoort zijn. Als we deze cijfers in de vergelijking voor x stoppen, krijgen we altijd een antwoord van minder dan 3.
- Met de vergelijking 3> 5x - 2 zouden we bijvoorbeeld oplossen zoals we zouden doen voor een normale vergelijking:
-
 3 Neem kwadratische vergelijkingen aan. Een algebraonderwerp waar veel beginners mee worstelen, is het oplossen van kwadratische vergelijkingen. Quadratics zijn vergelijkingen met de vormbijl2 + bx + c = 0, waarbij a, b en c getallen zijn (behalve dat a geen 0 kan zijn.) Deze vergelijkingen worden opgelost met de formule x = [-b +/- √ (b2 - 4ac)] / 2a. Wees voorzichtig - het +/- teken betekent dat je de antwoorden moet vinden om toe te voegen en aftrekken, zodat u twee antwoorden voor dit soort problemen kunt hebben.
3 Neem kwadratische vergelijkingen aan. Een algebraonderwerp waar veel beginners mee worstelen, is het oplossen van kwadratische vergelijkingen. Quadratics zijn vergelijkingen met de vormbijl2 + bx + c = 0, waarbij a, b en c getallen zijn (behalve dat a geen 0 kan zijn.) Deze vergelijkingen worden opgelost met de formule x = [-b +/- √ (b2 - 4ac)] / 2a. Wees voorzichtig - het +/- teken betekent dat je de antwoorden moet vinden om toe te voegen en aftrekken, zodat u twee antwoorden voor dit soort problemen kunt hebben. - Laten we als voorbeeld de kwadratische formule 3x oplossen2 + 2x -1 = 0.
-
- x = [-b +/- √ (b2 - 4ac)] / 2a
- x = [-2 +/- √ (22 - 4(3)(-1))]/2(3)
- x = [-2 +/- √ (4 - (-12))] / 6
- x = [-2 +/- √ (16)] / 6
- x = [-2 +/- 4] / 6
- x = -1 en 1/3
-
- Laten we als voorbeeld de kwadratische formule 3x oplossen2 + 2x -1 = 0.
-
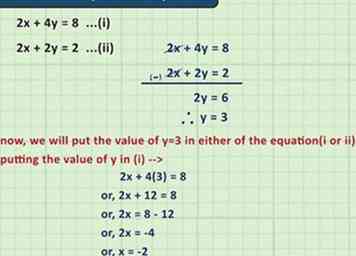 4 Experimenteer met systemen van vergelijkingen. Meer dan één vergelijking tegelijk oplossen klinkt misschien super-lastig, maar als je met eenvoudige algebra-vergelijkingen werkt, is het niet zo moeilijk. Vaak gebruiken algebra leraren een grafische benadering om deze problemen op te lossen. Wanneer u met een systeem van twee vergelijkingen werkt, zijn de oplossingen de punten in een grafiek die de lijnen voor beide vergelijkingen overschrijden.
4 Experimenteer met systemen van vergelijkingen. Meer dan één vergelijking tegelijk oplossen klinkt misschien super-lastig, maar als je met eenvoudige algebra-vergelijkingen werkt, is het niet zo moeilijk. Vaak gebruiken algebra leraren een grafische benadering om deze problemen op te lossen. Wanneer u met een systeem van twee vergelijkingen werkt, zijn de oplossingen de punten in een grafiek die de lijnen voor beide vergelijkingen overschrijden. - Laten we bijvoorbeeld zeggen dat we werken met een systeem dat de vergelijkingen y = 3x - 2 en y = -x - 6 bevat. Als we deze twee lijnen in een grafiek tekenen, krijgen we een lijn die omhoog gaat in een steile hoek en een die onder een milde hoek naar beneden gaat. Omdat deze lijnen elkaar kruisen op het punt (-1,-5), dit is een oplossing voor het systeem.[1]
- Als we ons probleem willen controleren, kunnen we dit doen door ons antwoord aan te vullen met de vergelijkingen in het systeem - een goed antwoord zou voor beide moeten "werken".
-
- y = 3x - 2
- -5 = 3(-1) - 2
- -5 = -3 - 2
- -5 = -5
- y = -x - 6
- -5 = -(-1) - 6
- -5 = 1 - 6
- -5 = -5
-
- Beide vergelijkingen "check out", dus ons antwoord is goed!
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Bekijk je basis wiskundige bewerkingen. Om algebra te leren leren, moet je basisvaardigheden voor wiskunde kennen, zoals optellen, aftrekken, vermenigvuldigen en delen. Deze wiskunde op de basis- / basisschool is essentieel voordat je begint met het leren van de algebra. Als je deze vaardigheden niet beheerst, zal het lastig zijn om de complexere concepten uit de algebra aan te pakken. Als je een opfrissing nodig hebt bij deze operaties, probeer dan ons artikel over elementaire wiskundige vaardigheden.
1 Bekijk je basis wiskundige bewerkingen. Om algebra te leren leren, moet je basisvaardigheden voor wiskunde kennen, zoals optellen, aftrekken, vermenigvuldigen en delen. Deze wiskunde op de basis- / basisschool is essentieel voordat je begint met het leren van de algebra. Als je deze vaardigheden niet beheerst, zal het lastig zijn om de complexere concepten uit de algebra aan te pakken. Als je een opfrissing nodig hebt bij deze operaties, probeer dan ons artikel over elementaire wiskundige vaardigheden.  2 Ken de volgorde van operaties. Een van de lastigste dingen over het oplossen van een algebra-vergelijking als beginner is weten waar te beginnen. Gelukkig is er een specifieke volgorde voor het oplossen van deze problemen: doe eerst wiskundige bewerkingen tussen haakjes, dan exponenten, vermenigvuldig dan, deel dan, voeg dan toe en tenslotte af. Een handig hulpmiddel voor het onthouden van deze volgorde van bewerkingen is het acroniem PEMDAS. Leer hier hoe u de volgorde van bewerkingen kunt toepassen. Om samen te vatten, is de volgorde van bewerkingen:
2 Ken de volgorde van operaties. Een van de lastigste dingen over het oplossen van een algebra-vergelijking als beginner is weten waar te beginnen. Gelukkig is er een specifieke volgorde voor het oplossen van deze problemen: doe eerst wiskundige bewerkingen tussen haakjes, dan exponenten, vermenigvuldig dan, deel dan, voeg dan toe en tenslotte af. Een handig hulpmiddel voor het onthouden van deze volgorde van bewerkingen is het acroniem PEMDAS. Leer hier hoe u de volgorde van bewerkingen kunt toepassen. Om samen te vatten, is de volgorde van bewerkingen: 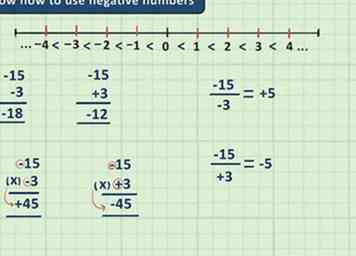 3 Weet hoe je negatieve getallen moet gebruiken. In algebra is het gebruikelijk om negatieve getallen te gebruiken, dus het is slim om te bekijken hoe je negatieven optelt, aftrekt, vermenigvuldigt en deelt voordat je begint met het leren van algebra. Hieronder staan slechts enkele basisprincipes met negatieve getallen om in gedachten te houden. Zie voor meer informatie onze artikelen over het toevoegen en aftrekken van negatieve getallen en het delen en vermenigvuldigen van negatieve getallen.
3 Weet hoe je negatieve getallen moet gebruiken. In algebra is het gebruikelijk om negatieve getallen te gebruiken, dus het is slim om te bekijken hoe je negatieven optelt, aftrekt, vermenigvuldigt en deelt voordat je begint met het leren van algebra. Hieronder staan slechts enkele basisprincipes met negatieve getallen om in gedachten te houden. Zie voor meer informatie onze artikelen over het toevoegen en aftrekken van negatieve getallen en het delen en vermenigvuldigen van negatieve getallen.  4 Weet hoe je lange problemen georganiseerd kunt houden. Hoewel eenvoudige algebra problemen een fluitje van een cent kunnen zijn om op te lossen, kunnen meer gecompliceerde problemen vele, vele stappen vereisen. Om fouten te voorkomen, moet u uw werk georganiseerd houden door een nieuwe regel te beginnen elke keer dat u een stap zet in de richting van het oplossen van uw probleem. Als je te maken hebt met een tweezijdige vergelijking, probeer dan alle gelijktekens ("=" s) onder elkaar te schrijven. Op deze manier, als je ergens een fout maakt, zal het veel gemakkelijker te vinden en corrigeren zijn.
4 Weet hoe je lange problemen georganiseerd kunt houden. Hoewel eenvoudige algebra problemen een fluitje van een cent kunnen zijn om op te lossen, kunnen meer gecompliceerde problemen vele, vele stappen vereisen. Om fouten te voorkomen, moet u uw werk georganiseerd houden door een nieuwe regel te beginnen elke keer dat u een stap zet in de richting van het oplossen van uw probleem. Als je te maken hebt met een tweezijdige vergelijking, probeer dan alle gelijktekens ("=" s) onder elkaar te schrijven. Op deze manier, als je ergens een fout maakt, zal het veel gemakkelijker te vinden en corrigeren zijn.  1 Zoek naar symbolen die geen nummers zijn. In de algebra zie je letters en symbolen verschijnen in je wiskundige problemen, in plaats van alleen cijfers. Dit worden variabelen genoemd. Variabelen zijn niet zo verwarrend als ze misschien lijken - het zijn gewoon manieren om getallen met onbekende waarden te tonen. Hieronder staan slechts enkele algemene voorbeelden van variabelen in de algebra:
1 Zoek naar symbolen die geen nummers zijn. In de algebra zie je letters en symbolen verschijnen in je wiskundige problemen, in plaats van alleen cijfers. Dit worden variabelen genoemd. Variabelen zijn niet zo verwarrend als ze misschien lijken - het zijn gewoon manieren om getallen met onbekende waarden te tonen. Hieronder staan slechts enkele algemene voorbeelden van variabelen in de algebra:  2 Beschouw variabelen als "onbekende" getallen. Zoals hierboven vermeld, zijn variabelen in feite gewoon cijfers met onbekende waarden. Met andere woorden, er is een nummer dat kan in de plaats van de variabele gaan om de vergelijking te laten werken. Meestal is je doel in een algebra-probleem om erachter te komen wat de variabele is - denk eraan als een "mysterienummer" dat je probeert te ontdekken.
2 Beschouw variabelen als "onbekende" getallen. Zoals hierboven vermeld, zijn variabelen in feite gewoon cijfers met onbekende waarden. Met andere woorden, er is een nummer dat kan in de plaats van de variabele gaan om de vergelijking te laten werken. Meestal is je doel in een algebra-probleem om erachter te komen wat de variabele is - denk eraan als een "mysterienummer" dat je probeert te ontdekken.  3 Let op terugkerende variabelen. Als een variabele meer dan eens verschijnt, vereenvoudig dan de variabelen. Wat doe je als dezelfde variabele meer dan eens voorkomt in de vergelijking? Hoewel deze situatie lastig lijkt om op te lossen, kunt u variabelen eigenlijk behandelen hoe u normale getallen behandelt. Met andere woorden, u kunt ze toevoegen, aftrekken, enzovoort, zolang u alleen variabelen combineert die op elkaar lijken. Met andere woorden, x + x = 2x, maar x + y is niet gelijk aan 2xy.
3 Let op terugkerende variabelen. Als een variabele meer dan eens verschijnt, vereenvoudig dan de variabelen. Wat doe je als dezelfde variabele meer dan eens voorkomt in de vergelijking? Hoewel deze situatie lastig lijkt om op te lossen, kunt u variabelen eigenlijk behandelen hoe u normale getallen behandelt. Met andere woorden, u kunt ze toevoegen, aftrekken, enzovoort, zolang u alleen variabelen combineert die op elkaar lijken. Met andere woorden, x + x = 2x, maar x + y is niet gelijk aan 2xy.  1 Probeer de variabele alleen in algebra-vergelijkingen te krijgen. Het oplossen van een vergelijking in de algebra betekent meestal dat je moet uitvinden wat de variabele is. Algebra-vergelijkingen worden meestal ingesteld met cijfers en / of variabelen aan beide zijden, zoals deze: x + 2 = 9 × 4. Om erachter te komen wat de variabele is, moet u hem alleen aan de ene kant van het gelijkteken krijgen. Wat er nog over is aan de andere kant van het gelijkteken is jouw antwoord.
1 Probeer de variabele alleen in algebra-vergelijkingen te krijgen. Het oplossen van een vergelijking in de algebra betekent meestal dat je moet uitvinden wat de variabele is. Algebra-vergelijkingen worden meestal ingesteld met cijfers en / of variabelen aan beide zijden, zoals deze: x + 2 = 9 × 4. Om erachter te komen wat de variabele is, moet u hem alleen aan de ene kant van het gelijkteken krijgen. Wat er nog over is aan de andere kant van het gelijkteken is jouw antwoord.  2 Annuleer toevoeging met aftrekken (en omgekeerd). Zoals we zojuist hierboven zagen, betekent het feit dat x alleen aan de ene kant van het gelijkteken staat, dat je de getallen ernaast weggooit. Om dit te doen, voeren we de "tegenovergestelde" bewerking uit aan beide zijden van de vergelijking. Bijvoorbeeld, in de vergelijking x + 3 = 0, omdat we een "+ 3" naast onze x zien, zullen we aan beide kanten een "- 3" plaatsen. De "+ 3" en "- 3", waarbij x zichzelf en "-3" aan de andere kant van het gelijkteken verlaten, zoals deze: x = -3.
2 Annuleer toevoeging met aftrekken (en omgekeerd). Zoals we zojuist hierboven zagen, betekent het feit dat x alleen aan de ene kant van het gelijkteken staat, dat je de getallen ernaast weggooit. Om dit te doen, voeren we de "tegenovergestelde" bewerking uit aan beide zijden van de vergelijking. Bijvoorbeeld, in de vergelijking x + 3 = 0, omdat we een "+ 3" naast onze x zien, zullen we aan beide kanten een "- 3" plaatsen. De "+ 3" en "- 3", waarbij x zichzelf en "-3" aan de andere kant van het gelijkteken verlaten, zoals deze: x = -3.  3 Annuleer vermenigvuldiging met delen (en omgekeerd). Vermenigvuldigen en delen zijn een beetje moeilijker om mee te werken dan optellen en aftrekken, maar ze hebben dezelfde "tegenovergestelde" relatie. Als u een "× 3" aan één kant ziet, annuleert u deze door beide zijden te delen door 3, enzovoort.
3 Annuleer vermenigvuldiging met delen (en omgekeerd). Vermenigvuldigen en delen zijn een beetje moeilijker om mee te werken dan optellen en aftrekken, maar ze hebben dezelfde "tegenovergestelde" relatie. Als u een "× 3" aan één kant ziet, annuleert u deze door beide zijden te delen door 3, enzovoort.  4 Annuleer exponenten door de root te nemen (en omgekeerd). Exponenten zijn een vrij uitgebreid pre-algebra-onderwerp - als je niet weet hoe je dit moet doen, bekijk je ons basis exponentartikel voor meer informatie. Het "tegenovergestelde" van een exponent is de wortel die hetzelfde nummer heeft. Bijvoorbeeld het tegenovergestelde van de 2 exponent is een vierkantswortel (√), het tegenovergestelde van de 3 exponent is de kubuswortel (3√), enzovoort.
4 Annuleer exponenten door de root te nemen (en omgekeerd). Exponenten zijn een vrij uitgebreid pre-algebra-onderwerp - als je niet weet hoe je dit moet doen, bekijk je ons basis exponentartikel voor meer informatie. Het "tegenovergestelde" van een exponent is de wortel die hetzelfde nummer heeft. Bijvoorbeeld het tegenovergestelde van de 2 exponent is een vierkantswortel (√), het tegenovergestelde van de 3 exponent is de kubuswortel (3√), enzovoort.  1 Gebruik foto's om problemen duidelijker te maken. Als je het moeilijk hebt om een algebra-probleem te visualiseren, probeer dan diagrammen of afbeeldingen te gebruiken om je vergelijking te illustreren. Je kunt zelfs proberen om een groep fysieke objecten (zoals blokken of munten) te gebruiken als je wat handig hebt.
1 Gebruik foto's om problemen duidelijker te maken. Als je het moeilijk hebt om een algebra-probleem te visualiseren, probeer dan diagrammen of afbeeldingen te gebruiken om je vergelijking te illustreren. Je kunt zelfs proberen om een groep fysieke objecten (zoals blokken of munten) te gebruiken als je wat handig hebt.  2 Gebruik "gezond verstand" (vooral voor woordproblemen). Wanneer u een woordprobleem in algebra converteert, probeert u uw formule te controleren door eenvoudige waarden voor uw variabele in te voegen. Heeft uw vergelijking zin als x = 0? Wanneer x = 1? Wanneer x = -1? Het is gemakkelijk om eenvoudige fouten te maken door p = 6d op te schrijven als je p = d / 6 bedoelt, maar deze worden gemakkelijk gepakt als je een snelle sanitaire controle op je werk uitvoert voordat je verder gaat.
2 Gebruik "gezond verstand" (vooral voor woordproblemen). Wanneer u een woordprobleem in algebra converteert, probeert u uw formule te controleren door eenvoudige waarden voor uw variabele in te voegen. Heeft uw vergelijking zin als x = 0? Wanneer x = 1? Wanneer x = -1? Het is gemakkelijk om eenvoudige fouten te maken door p = 6d op te schrijven als je p = d / 6 bedoelt, maar deze worden gemakkelijk gepakt als je een snelle sanitaire controle op je werk uitvoert voordat je verder gaat.  3 Houd er rekening mee dat antwoorden niet altijd gehele getallen in de algebra zijn. Antwoorden in algebra en andere geavanceerde vormen van wiskunde zijn niet altijd ronde, gemakkelijke getallen. Ze kunnen vaak decimalen, breuken of irrationele getallen zijn. Een rekenmachine kan je helpen deze gecompliceerde antwoorden te vinden, maar houd er rekening mee dat je leraar je misschien vraagt om je antwoord in de exacte vorm te geven, niet in een log decimaal.
3 Houd er rekening mee dat antwoorden niet altijd gehele getallen in de algebra zijn. Antwoorden in algebra en andere geavanceerde vormen van wiskunde zijn niet altijd ronde, gemakkelijke getallen. Ze kunnen vaak decimalen, breuken of irrationele getallen zijn. Een rekenmachine kan je helpen deze gecompliceerde antwoorden te vinden, maar houd er rekening mee dat je leraar je misschien vraagt om je antwoord in de exacte vorm te geven, niet in een log decimaal.  4 Probeer je vaardigheden uit te breiden. Als je zeker bent van elementaire algebra, probeer dan factoring. Een van de lastigste algebravaardigheden van allemaal is factoring - een soort snelkoppeling voor het verkrijgen van complexe vergelijkingen in eenvoudige vormen. Factoring is een semi-geavanceerd algebra-onderwerp. Overweeg daarom het bovenstaande artikel te raadplegen als u problemen ondervindt om het te beheersen. Hieronder staan slechts een paar snelle tips voor factoring-vergelijkingen:
4 Probeer je vaardigheden uit te breiden. Als je zeker bent van elementaire algebra, probeer dan factoring. Een van de lastigste algebravaardigheden van allemaal is factoring - een soort snelkoppeling voor het verkrijgen van complexe vergelijkingen in eenvoudige vormen. Factoring is een semi-geavanceerd algebra-onderwerp. Overweeg daarom het bovenstaande artikel te raadplegen als u problemen ondervindt om het te beheersen. Hieronder staan slechts een paar snelle tips voor factoring-vergelijkingen:  5 Oefenen, oefenen, oefenen! Vooruitgang in de algebra (en elke andere vorm van wiskunde) vereist veel hard werk en herhaling. Maak je geen zorgen - door al je opdrachten in de klas te volgen en hulp te zoeken van je leraar of andere studenten wanneer je het nodig hebt, zal de algebra een tweede natuur worden.
5 Oefenen, oefenen, oefenen! Vooruitgang in de algebra (en elke andere vorm van wiskunde) vereist veel hard werk en herhaling. Maak je geen zorgen - door al je opdrachten in de klas te volgen en hulp te zoeken van je leraar of andere studenten wanneer je het nodig hebt, zal de algebra een tweede natuur worden.  6 Vraag je leraar om je te helpen bij het begrijpen van lastige algebra-onderwerpen. Als je het moeilijk hebt om algebra onder de knie te krijgen, maak je geen zorgen - je hoeft het niet alleen te leren. Je leraar is de eerste persoon waar je terecht moet met vragen. Vraag na de les je leraar vriendelijk om hulp. Goede leraren zijn meestal bereid om het onderwerp van de dag opnieuw uit te leggen op een afspraak na de school en kunnen je misschien zelfs extra oefenmateriaal geven.
6 Vraag je leraar om je te helpen bij het begrijpen van lastige algebra-onderwerpen. Als je het moeilijk hebt om algebra onder de knie te krijgen, maak je geen zorgen - je hoeft het niet alleen te leren. Je leraar is de eerste persoon waar je terecht moet met vragen. Vraag na de les je leraar vriendelijk om hulp. Goede leraren zijn meestal bereid om het onderwerp van de dag opnieuw uit te leggen op een afspraak na de school en kunnen je misschien zelfs extra oefenmateriaal geven.  1 Leer x / y-vergelijkingen te maken. Grafieken kunnen waardevolle hulpmiddelen in de algebra zijn, omdat ze u in staat stellen ideeën weer te geven waarvoor u normaal gesproken getallen nodig heeft in gemakkelijk te begrijpen afbeeldingen. Gewoonlijk zijn grafische problemen in de beginalgebra beperkt tot vergelijkingen met twee variabelen (meestal x en y) en worden ze uitgevoerd op een eenvoudige 2-D grafiek met een x-as en een y-as. Met deze vergelijkingen hoeft u alleen maar een waarde in te voeren voor x en vervolgens op te lossen voor y (of omgekeerd) om twee getallen te krijgen die overeenkomen met een punt in de grafiek.
1 Leer x / y-vergelijkingen te maken. Grafieken kunnen waardevolle hulpmiddelen in de algebra zijn, omdat ze u in staat stellen ideeën weer te geven waarvoor u normaal gesproken getallen nodig heeft in gemakkelijk te begrijpen afbeeldingen. Gewoonlijk zijn grafische problemen in de beginalgebra beperkt tot vergelijkingen met twee variabelen (meestal x en y) en worden ze uitgevoerd op een eenvoudige 2-D grafiek met een x-as en een y-as. Met deze vergelijkingen hoeft u alleen maar een waarde in te voeren voor x en vervolgens op te lossen voor y (of omgekeerd) om twee getallen te krijgen die overeenkomen met een punt in de grafiek.  2 Leer ongelijkheden op te lossen. Wat doe je als je vergelijking geen gelijkteken gebruikt? Niets anders dan wat je normaal zou doen, blijkt. Voor ongelijkheden, die tekens gebruiken als> ("groter dan") en <("minder dan"), lost u gewoon op zoals normaal. Je blijft zitten met een antwoord dat kleiner of groter is dan je variabele.
2 Leer ongelijkheden op te lossen. Wat doe je als je vergelijking geen gelijkteken gebruikt? Niets anders dan wat je normaal zou doen, blijkt. Voor ongelijkheden, die tekens gebruiken als> ("groter dan") en <("minder dan"), lost u gewoon op zoals normaal. Je blijft zitten met een antwoord dat kleiner of groter is dan je variabele.  3 Neem kwadratische vergelijkingen aan. Een algebraonderwerp waar veel beginners mee worstelen, is het oplossen van kwadratische vergelijkingen. Quadratics zijn vergelijkingen met de vormbijl2 + bx + c = 0, waarbij a, b en c getallen zijn (behalve dat a geen 0 kan zijn.) Deze vergelijkingen worden opgelost met de formule x = [-b +/- √ (b2 - 4ac)] / 2a. Wees voorzichtig - het +/- teken betekent dat je de antwoorden moet vinden om toe te voegen en aftrekken, zodat u twee antwoorden voor dit soort problemen kunt hebben.
3 Neem kwadratische vergelijkingen aan. Een algebraonderwerp waar veel beginners mee worstelen, is het oplossen van kwadratische vergelijkingen. Quadratics zijn vergelijkingen met de vormbijl2 + bx + c = 0, waarbij a, b en c getallen zijn (behalve dat a geen 0 kan zijn.) Deze vergelijkingen worden opgelost met de formule x = [-b +/- √ (b2 - 4ac)] / 2a. Wees voorzichtig - het +/- teken betekent dat je de antwoorden moet vinden om toe te voegen en aftrekken, zodat u twee antwoorden voor dit soort problemen kunt hebben. 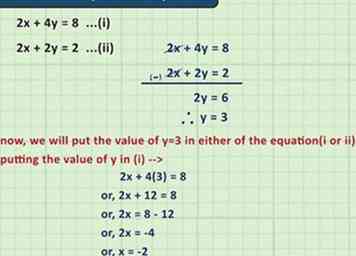 4 Experimenteer met systemen van vergelijkingen. Meer dan één vergelijking tegelijk oplossen klinkt misschien super-lastig, maar als je met eenvoudige algebra-vergelijkingen werkt, is het niet zo moeilijk. Vaak gebruiken algebra leraren een grafische benadering om deze problemen op te lossen. Wanneer u met een systeem van twee vergelijkingen werkt, zijn de oplossingen de punten in een grafiek die de lijnen voor beide vergelijkingen overschrijden.
4 Experimenteer met systemen van vergelijkingen. Meer dan één vergelijking tegelijk oplossen klinkt misschien super-lastig, maar als je met eenvoudige algebra-vergelijkingen werkt, is het niet zo moeilijk. Vaak gebruiken algebra leraren een grafische benadering om deze problemen op te lossen. Wanneer u met een systeem van twee vergelijkingen werkt, zijn de oplossingen de punten in een grafiek die de lijnen voor beide vergelijkingen overschrijden.