Hoe te integreren

Integratie is de omgekeerde werking van differentiatie. Er wordt vaak gezegd dat differentiatie een wetenschap is, terwijl integratie een kunst is. De reden is omdat integratie eenvoudigweg een moeilijkere taak is om te doen - terwijl een afgeleide zich alleen bezighoudt met het gedrag van een functie op een punt, een integraal, zijnde een veredelde som, vereist globaal kennis van de functie. Dus hoewel er enkele functies zijn waarvan de integralen kunnen worden geëvalueerd met behulp van de standaardtechnieken in dit artikel, kunnen veel meer niet.

We behandelen de basistechnieken van integratie met één variabele in dit artikel en passen deze toe op functies met antiderivatieven.

Deel een van de zeven:
De basis

1. 1 Begrijp de notatie voor integratie. Een integraal $\ displaystyle \ int _ a ^ b f (x) \ mathrm d x$ bestaat uit vier delen.
   • De $\ displaystyle \ int$ is het symbool voor integratie. Het is eigenlijk een langgerekte S.
   • De functie $\ displaystyle f (x)$ wordt het integrand wanneer het zich in de integraal bevindt.
   • Het verschil $\ displaystyle \ mathrm d x$ intuïtief is zeggen welke variabele je integreert ten opzichte van. Omdat (Riemann) integratie slechts een optelsom is van oneindig klein dunne rechthoeken met een hoogte van $\ displaystyle f (x),$ we zien dat $\ displaystyle \ mathrm d x$ verwijst naar de breedte van die rechthoeken.
   • De brieven $\ displaystyle a$ en $\ displaystyle b$ zijn de grenzen. Een integraal hoeft geen grenzen te hebben. Wanneer dit het geval is, zeggen we dat we te maken hebben met een onbepaalde integraal. Als dat zo is, hebben we te maken met een bepaalde integraal.
   • In dit artikel zullen we het zoekproces bespreken primitieve functie van een functie. Een antiderivatief is een functie waarvan de afgeleide de oorspronkelijke functie is waarmee we zijn begonnen.
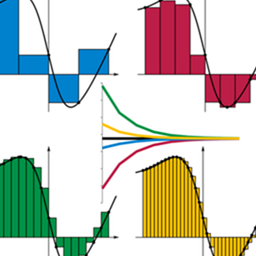2. 2 Begrijp de definitie van een integraal. Als we het hebben over integralen, verwijzen we meestal naar Riemann integralen; met andere woorden, rechthoeken opsommen. Gegeven een functie $\ displaystyle f (x),$ een rechthoekbreedte van $\ displaystyle \ Delta x,$ en een interval $\ displaystyle [a, b],$ het gebied van de eerste rechthoek wordt gegeven door $\ displaystyle f (x_ 1) \ Delta x_ 1,$ omdat het gewoon de basistijden is van de hoogte (de waarde van de functie). Evenzo is het gebied van de tweede rechthoek $\ displaystyle f (x_ 2) \ Delta x_ 2.$ Generaliseren, we zeggen het gebied van de ith rechthoek is $\ displaystyle f (x_ i) \ Delta x_ i.$ In sommatie-notatie kan dit op de volgende manier worden weergegeven.
   • $\ displaystyle \ sum _ i = 1 ^ n f (x_ i) \ Delta x_ i$
   • Als dit de eerste keer is dat je een sommatie-symbool hebt gezien, ziet het er misschien eng uit ... maar het is helemaal niet gecompliceerd. Dit zegt alleen maar dat we het gebied samenvatten $\ displaystyle n$ rechthoeken. (De variabele $\ displaystyle i$ staat bekend als een dummy-index.) Zoals u wel kunt raden, is het gebied van alle rechthoeken waarschijnlijk iets anders dan het werkelijke gebied. We lossen dit op door het aantal rechthoeken naar het oneindige te sturen. Naarmate we het aantal rechthoeken vergroten, benadert het gebied van alle rechthoeken het gebied onder de curve beter. Dat is wat het diagram hierboven laat zien (zie de tips voor wat de grafiek in het midden toont). De limiet als $\ displaystyle n \ to \ infty$ is wat we definiëren als de integraal van de functie $\ displaystyle f (x)$ van $\ displaystyle a$ naar $\ displaystyle b.$
     • $\ displaystyle \ int _ a ^ b f (x) \ mathrm d x = \ lim _ n \ to \ infty \ sum _ i = 1 ^ n f ( x_ i) \ Delta x_ i$
   • Natuurlijk moet deze limiet bestaan ​​om de integraal enige betekenis te geven. Als zo'n limiet niet bestaat op het interval, dan zeggen we dat $\ displaystyle f (x)$ heeft geen integraal over het interval $\ displaystyle [a, b].$ In dit artikel (en in bijna elke fysieke toepassing) behandelen we alleen functies waarbij deze integralen bestaan.
3. 3 Onthouden $\ displaystyle + C$ bij het evalueren van onbepaalde integralen! Een van de meest voorkomende fouten die mensen kunnen maken, is vergeten de constante van integratie toe te voegen. De reden waarom dit nodig is, is omdat antiderivatieven niet uniek zijn. In feite kan een functie een oneindig aantal antiderivatieven hebben. Ze zijn toegestaan ​​omdat de afgeleide van een constante 0 is.

Deel twee van zeven:
Krachtregel

1. 1 Overweeg een monomiaal $\ displaystyle x ^ n$.
2. 2 Voer de power-regel uit voor integralen. Dit is dezelfde machtsregel voor derivaten, maar dan omgekeerd. We vergroten het vermogen met 1 en delen het nieuwe vermogen. Vergeet niet om de constante van integratie toe te voegen $\ displaystyle C.$
   • $\ displaystyle \ int x ^ n \ mathrm d x = \ frac x ^ n + 1 n + 1 + C$
   • Om te verifiëren dat deze machtsregel geldt, onderscheidt u het antiderivatief om de oorspronkelijke functie te herstellen.
   • De machtsregel geldt voor alle functies van deze vorm met mate $\ displaystyle n$ behalve wanneer $\ displaystyle n = -1.$ We zullen later zien waarom.
3. 3 Pas lineariteit toe. Integratie is een lineaire operator, wat betekent dat de integraal van een som de som is van de integralen, en de coëfficiënt van elke term kan worden weggelaten, zoals:
   • $\ displaystyle \ int (ax ^ n + bx ^ m) \ mathrm d x = a \ int x ^ n \ mathrm d x + b \ int x ^ m \ mathrm d x$
   • Dit zou bekend moeten zijn omdat het derivaat ook een lineaire operator is; het derivaat van een som is de som van de derivaten.
   • Lineariteit is niet alleen van toepassing op integralen van polynomen. Het is van toepassing op elke integraal waarbij de integrand een som is van twee of meer termen.
4. 4 Zoek de antiderivative van de functie $\ displaystyle f (x) = x ^ 4 + 2x ^ 3 -5x ^ 2 -1$. Dit is een polynoom, dus met behulp van de eigenschap van lineariteit en de machtsregel kan het antiderivaat gemakkelijk worden berekend. Om het antiderivatief van een constante te vinden, onthoud dat $\ displaystyle x ^ 0 = 1,$ dus de constante is eigenlijk gewoon de coëfficiënt van $\ displaystyle x ^ 0.$
   • $\ displaystyle \ int (x ^ 4 + 2x ^ 3 -5x ^ 2 -1) \ mathrm d x = \ frac 1 5 x ^ 5 + \ frac 2 4 x ^ 4 - \ frac 5 3 x ^ 3 -x + C$
5. 5 Zoek de antiderivative van de functie $\ displaystyle f (x) = \ frac 2x ^ 2 + 3x-1 x ^ 1/3$. Dit lijkt misschien een functie die onze regels tart, maar de blik van een moment onthult dat we de breuk in drie breuken kunnen scheiden en lineariteit en de machtsregel kunnen toepassen om het antiderivaat te vinden.
   • $\ displaystyle \ begin uitgelijnd \ int f (x) \ mathrm d x & = \ int \ frac 2x ^ 2 + 3x-1 x ^ 1/3 \ mathrm d x \ & = \ int \ left (\ frac 2x ^ 2 x ^ 1/3 + \ frac 3x x ^ 1 / 3 - \ frac 1 x ^ 1/3 \ right) \ mathrm d x \ & = \ int (2x ^ 5/3 + 3x ^ 2/3 -x ^ - 1/3) \ mathrm d x \ & = 2 \ cdot \ frac 3 8 x ^ 8/3 +3 \ cdot \ frac 3 5 x ^ 5/3 - \ frac 3 2 x ^ 2/3 + C \ & = \ frac 3 4 x ^ 8/3 + \ frac 9 5 x ^ 5/3 - \ frac 3 2 x ^ 2/3 + C \ end aligned$
   • Het algemene thema is dat je alle manipulaties moet uitvoeren om de integraal in een polynoom te krijgen. Vanaf daar is integratie eenvoudig. Te oordelen of de integraal gemakkelijk genoeg is voor brute kracht, of eerst enige algebraïsche manipulatie vereist, is waar de vaardigheid ligt.

Deel drie van zeven:
Bepaalde integratie

1. 1 Beschouw de integraal hieronder. In tegenstelling tot het integratieproces in deel 2, hebben we ook grenzen om te evalueren op.
   • $\ displaystyle \ int _ 2 ^ 3 x ^ 2 \ mathrm d x$
2. 2 Gebruik de fundamentele stelling van calculus. Deze stelling bestaat uit twee delen. Het eerste deel stond in de eerste zin van dit artikel: integratie is de inverse bewerking van differentiatie, dus het integreren en vervolgens differentiëren van een functie herstelt de oorspronkelijke functie. Het tweede deel staat hieronder.
   • Laat $\ displaystyle F (x)$ wees een antiderivative van $\ displaystyle f (x).$ Dan $\ displaystyle \ int _ a ^ b f (x) \ mathrm d x = F (b) -F (a).$
   • Deze stelling is ongelooflijk nuttig omdat het de integraal vereenvoudigt en betekent dat de bepaalde integraal is volledig bepaald alleen de waarden op de grenzen. Het is niet nodig om rechthoeken opnieuw samen te vatten om integralen te berekenen. Alles wat we nu moeten doen is antiderivatieven vinden en evalueren op de grenzen!
3. 3 Evalueer de in stap 1 vermelde integraal. Nu we de fundamentele stelling hebben als een hulpmiddel voor het oplossen van integralen, kunnen we eenvoudig de waarde van de integraal berekenen zoals hierboven gedefinieerd.
   • $\ displaystyle \ start aligned \ int _ 2 ^ 3 x ^ 2 \ mathrm d x & = \ frac 1 3 x ^ 3 \ Bigg | _ 2 ^ 3 \ & = \ frac 1 3 (3) ^ 3 - \ frac 1 3 (2) ^ 3 \ & = \ frac 19 3 \ end aligned$
   • Nogmaals, de fundamentele stelling van calculus is niet alleen van toepassing op functies als $\ displaystyle f (x) = x ^ 2.$ De fundamentele stelling kan worden gebruikt om te integreren ieder functie, zolang je een antiderivatief kunt vinden.
4. 4 Evalueer de integraal met de omgewisselde grenzen. Laten we kijken wat hier gebeurt.
   • $\ displaystyle \ start aligned \ int _ 3 ^ 2 x ^ 2 \ mathrm d x & = \ frac 1 3 x ^ 3 \ Bigg | _ 3 ^ 2 \ & = \ frac 1 3 (2) ^ 3 - \ frac 1 3 (3) ^ 3 \ & = - \ frac 19 3 \ end aligned$
   • We hebben net het negatief van het antwoord gekregen dat we eerder kregen. Dit illustreert een belangrijke eigenschap van definitieve integralen. Als u de grenzen verwisselt, wordt de integraal genegeerd.
     • $\ displaystyle \ int _ b ^ a f (x) \ mathrm d x = - \ int _ a ^ b f (x) \ mathrm d x$

Deel vier van zeven:
Antiderivatives of Common Functions

1. 1 Onthoud de antiderivatieven van exponentiële functies. In de volgende stappen geven we veel voorkomende functies zoals de exponentiële en trigonometrische functies. Ze worden allemaal op grote schaal tegengekomen, dus weten wat hun antiderivatieven zijn, is cruciaal voor het opbouwen van integratievaardigheden. Vergeet niet dat onbepaalde integralen een extra hebben $\ displaystyle C,$ omdat de afgeleide van een constante 0 is.
   • $\ displaystyle \ int e ^ x \ mathrm d x = e ^ x + C$
   • $\ displaystyle \ int a ^ x \ mathrm d x = \ frac a ^ x \ ln a + C$
2. 2 Onthoud de antiderivatieven van trigonometrische functies. Dit zijn alleen de derivaten die achterwaarts worden toegepast en moeten vertrouwd zijn. De sinussen en cosinussen komen veel vaker voor en zouden dat ook moeten zijn definitief worden onthouden. Hyperbolische analogen worden op dezelfde manier gevonden, hoewel ze minder vaak worden aangetroffen.
   • $\ displaystyle \ int \ sin x \ mathrm d x = - \ cos x + C$
   • $\ displaystyle \ int \ cos x \ mathrm d x = \ sin x + C$
   • $\ displaystyle \ int \ sec ^ 2 x \ mathrm d x = \ tan x + C$
   • $\ displaystyle \ int \ csc ^ 2 x \ mathrm d x = - \ cot x + C$
   • $\ displaystyle \ int \ sec x \ tan x \ mathrm d x = \ sec x + C$
   • $\ displaystyle \ int \ csc x \ cot x \ mathrm d x = - \ csc x + C$
3. 3 Onthoud de antiderivatieven van inverse trigonometrische functies. Deze moeten niet echt worden beschouwd als een oefening in 'memoriseren'. Zolang u bekend bent met de derivaten, moeten de meeste van deze antiderivatieven ook bekend zijn.
   • $\ displaystyle \ int \ frac 1 \ sqrt 1-x ^ 2 \ mathrm d x = \ sin ^ - 1 x + C$
   • $\ displaystyle \ int \ frac -1 \ sqrt 1-x ^ 2 \ mathrm d x = \ cos ^ - 1 x + C$
   • $\ displaystyle \ int \ frac 1 1 + x ^ 2 \ mathrm d x = \ tan ^ - 1 x + C$
4. 4 Onthoud het antiderivatief van de wederkerige functie. Eerder hebben we gezegd dat de functie $\ displaystyle f (x) = x ^ - 1,$ of $\ displaystyle f (x) = \ frac 1 x,$ was een uitzondering op de machtsregel. De reden is dat het antiderivaat van deze functie de logaritmische functie is.
   • $\ displaystyle \ int \ frac 1 x \ mathrm d x = \ ln | x | + C$
   • (Soms zetten auteurs graag de $\ displaystyle \ mathrm d x$ in de teller van de breuk, dus het leest als: $\ displaystyle \ int \ frac \ mathrm d x x.$ Let op deze notatie.)
   • De reden voor de absolute waarde in de logaritmefunctie is subtiel en vereist een grondiger begrip van echte analyse om volledig te kunnen antwoorden. Voor nu, zullen we gewoon leven met het feit dat de domeinen hetzelfde worden wanneer de absolute waardenbalken worden toegevoegd.
5. 5 Evalueer de volgende integraal over de gegeven grenzen. Onze functie wordt gegeven als $\ displaystyle f (x) = 2 \ cos x + \ tan ^ 2 x-6.$ Hier weten we niet de antiderivatie van $\ displaystyle \ tan ^ 2 x,$ maar we kunnen een trigonometrische identiteit gebruiken om de integrand te herschrijven in termen van een functie waarvan we de antiderivatie kennen, namelijk: $\ displaystyle 1+ \ tan ^ 2 x = \ sec ^ 2 x.$
   • $\ displaystyle \ start aligned \ int _ \ pi / 4 ^ \ pi / 3 f (x) \ mathrm d x & = \ int _ \ pi / 4 ^ \ pi / 3 (2 \ cos x + \ tan ^ 2 x-6) \ mathrm d x \ & = \ int _ \ pi / 4 ^ \ pi / 3 (2 \ cos x + \ sec ^ 2 x-7) \ mathrm d x \ & = (2 \ sin x + \ tan x-7x) \ Big | _ \ pi / 4 ^ \ pi / 3 \ & = \ left (2 \ sin \ frac \ pi 3 + \ tan \ frac \ pi 3 - \ frac 7 \ pi 3 \ right) - \ left (2 \ sin \ frac \ pi 4 + \ tan\ frac \ pi 4 - \ frac 7 \ pi 4 \ right) \ & = 2 \ sqrt 3 - \ sqrt 2 - 1- \ frac 7 \ pi 12 \ end aligned$
   • Als u een decimale benadering nodig heeft, kunt u een rekenmachine gebruiken. Hier, $\ displaystyle 2 \ sqrt 3 - \ sqrt 2 - 1 - \ frac 7 \ pi 12 \ approx -0.7827.$

Deel vijf van zeven:
Integralen van symmetrische functies

1. 1 Evalueer de integraal van een even functie. Zelfs functies zijn functies met de eigenschap die $\ displaystyle f (-x) = f (x).$ Met andere woorden, je zou in staat moeten zijn om elke te vervangen $\ displaystyle x$ met een $\ displaystyle -x$ en krijg dezelfde functie. Een voorbeeld van een even functie is $\ displaystyle x ^ 2.$ Een ander voorbeeld is de cosinusfunctie. Alle even functies zijn symmetrisch rond de y-as.
   • $\ displaystyle \ int _ - 1 ^ 1 (\ cos x + x ^ 4) \ mathrm d x$
   • Onze integrand is zelfs. We kunnen onmiddellijk integreren door de fundamentele stelling van calculus te gebruiken, maar als we nauwkeuriger kijken, zien we dat de grenzen symmetrisch zijn over $\ displaystyle x = 0.$ Dat betekent dat de integraal van -1 tot 0 ons dezelfde waarde zal geven als de integraal van 0 tot 1. Dus wat we kunnen doen is dat we de grenzen kunnen wijzigen in 0 en 1 en een factor 2 weglaten.
     • $\ displaystyle \ int _ - 1 ^ 1 (\ cos x + x ^ 4) \ mathrm d x = 2 \ int _ 0 ^ 1 (\ cos x + x ^ 4) \ mathrm d x$
   • Het lijkt misschien niet veel om dit te doen, maar we zullen meteen zien dat ons werk vereenvoudigd is. Nadat u het antiderivatief heeft gevonden, merkt u dat we het alleen moeten evalueren op $\ displaystyle x = 1.$ De antiderivative op $\ displaystyle x = 0$ zullen niet bijdragen aan de integraal.
     • $\ displaystyle 2 \ int _ 0 ^ 1 (\ cos x + x ^ 4) \ mathrm d x = 2 \ sin 1 + \ frac 2 5$
   • Over het algemeen moet u elke keer dat u een even-functie met symmetrische grenzen ziet, deze vereenvoudiging uitvoeren om minder rekenfouten te maken.
     • $\ displaystyle \ int _ - a ^ a f (x) \ mathrm d x = 2 \ int _ 0 ^ a f (x) \ mathrm d x , \ \ f (x) \ \ mathrm even$
2. 2 Evalueer de integraal van een oneven functie. Vreemde functies zijn functies met de eigenschap die $\ displaystyle f (-x) = - f (x).$ Met andere woorden, je zou in staat moeten zijn om elke te vervangen $\ displaystyle x$ met een $\ displaystyle -x$ en pak dan de negatief van de oorspronkelijke functie. Een voorbeeld van een oneven functie is $\ displaystyle x ^ 3.$ De sinus- en tangensfuncties zijn ook vreemd. Alle oneven functies zijn symmetrisch rond de oorsprong (stel je voor dat het negatieve deel van de functie 180 ° wordt gedraaid - het zal dan bovenop het positieve deel van de functie worden gestapeld). Als de grenzen symmetrisch zijn, is de integraal 0.
   • $\ displaystyle \ int _ - \ pi / 2 ^ \ pi / 2 (2x ^ 3 +2 \ sin x) \ mathrm d x$
   • We zouden deze integraal rechtstreeks kunnen evalueren ... of we kunnen herkennen dat onze integrand vreemd is. Verder zijn de grenzen symmetrisch rond de oorsprong. Daarom is onze integraal 0. Waarom is dit het geval? Het is omdat het antiderivatief gelijk is. Zelfs functies hebben de eigenschap dat $\ displaystyle f (-x) = f (x),$ dus wanneer we evalueren op de grenzen $\ displaystyle -a$ en $\ displaystyle a,$ dan $\ displaystyle F (-a) = F (a)$ impliceert dat onmiddellijk $\ displaystyle F (a) -F (-a) = 0.$
     • $\ displaystyle \ int _ - \ pi / 2 ^ \ pi / 2 (2x ^ 3 +2 \ sin x) \ mathrm d x = 0$
   • De eigenschappen van deze functies zijn zeer krachtig in het vereenvoudigen van de integralen, maar de grenzen moet symmetrisch zijn. Anders moeten we de oude manier evalueren.
     • $\ displaystyle \ int _ - a ^ a f (x) \ mathrm d x = 0, \ \ f (x) \ \ mathrm odd$

Deel zes van zeven:
U-Substitutie

1. 1 Zie het hoofdartikel over het uitvoeren van u-vervangingen. U-substitutie is een techniek die variabelen verandert met de hoop een eenvoudiger integraal te krijgen. Zoals we zullen zien, is het de analogie van de kettingregel voor derivaten.
2. 2 Evalueer de integraal van $\ displaystyle e ^ axel$. Wat doen we wanneer de exponent een coëfficiënt bevat? We gebruiken u-vervanging om variabelen te wijzigen. Het blijkt dat dit soort u-subs het eenvoudigst uit te voeren zijn, en ze worden zo vaak gedaan, dat de u-sub vaak wordt overgeslagen. Niettemin zullen we het hele proces laten zien.
   • $\ displaystyle \ int e ^ ax \ mathrm d x$
3. 3 Kies een $\ displaystyle u$ en vind $\ displaystyle \ mathrm d u$. We kiezen $\ displaystyle u = ax$ zodat we een krijgen $\ displaystyle e ^ u$ in de integrand, een functie wiens antiderivatie we kennen - zelf. Dan moeten we vervangen $\ displaystyle \ mathrm d x$ met $\ displaystyle \ mathrm d u,$ maar we moeten ervoor zorgen dat we onze voorwaarden bijhouden. In dit voorbeeld $\ displaystyle \ mathrm d u = a \ mathrm d x,$ dus we moeten de hele integraal delen door $\ displaystyle a$ compenseren.
   • $\ displaystyle \ int e ^ ax \ mathrm d x = \ frac 1 a \ int e ^ u \ mathrm d u$
4. 4 Evalueer en herschrijf in termen van de oorspronkelijke variabele. Voor onbepaalde integralen moet u de oorspronkelijke variabele herschrijven.
   • $\ displaystyle \ int e ^ ax \ mathrm d x = \ frac 1 a e ^ ax + C$
5. 5 Evalueer de volgende integraal met de gegeven grenzen. Dit is een duidelijke integraal, dus we moeten het antiderivaat aan de grenzen evalueren. We zullen ook zien dat deze u-sub een geval is waarin u 'back-substitute' moet gebruiken.
   • $\ displaystyle \ int _ 0 ^ 1 x \ sqrt 2x + 3 \ mathrm d x$
6. 6 Kies een $\ displaystyle u$ en vind $\ displaystyle \ mathrm d u$. Zorg ervoor dat je ook je grenzen wijzigt, afhankelijk van je vervanging. We kiezen $\ displaystyle u = 2x + 3$ zodat we de vierkantswortel vereenvoudigen. Dan $\ displaystyle \ mathrm d u = 2 \ mathrm d x,$ en de grenzen gaan dan van 3 naar 5. Echter, na het vervangen van de $\ displaystyle \ mathrm d x$ met een $\ displaystyle \ mathrm d u,$ we hebben nog steeds een $\ displaystyle x$ in de integrand.
   • $\ displaystyle \ int _ 0 ^ 1 x \ sqrt 2x + 3 \ mathrm d x = \ frac 1 2 \ int _ 3 ^ 5 x \ sqrt u \ mathrm d u$
7. 7 Oplossen voor $\ displaystyle x$ aangaande met $\ displaystyle u$ en vervanger. Dit is de back-substitutie waar we het eerder over hadden. Onze u-sub heeft niet alle $\ displaystyle x$ termen in de integrand, dus we moeten een back-sub maken om er vanaf te komen. Dat vinden we $\ displaystyle x = \ frac u-3 2.$ Na het vereenvoudigen krijgen we het volgende.
   • $\ displaystyle \ frac 1 2 \ int _ 3 ^ 5 x \ sqrt u \ mathrm d u = \ frac 1 4 \ int _ 3 ^ 5 (u-3) \ sqrt u \ mathrm d u$
8. 8 Uitbreiden en evalueren. Een voordeel bij het omgaan met definitieve integralen is dat u het antiderivatief in termen van de oorspronkelijke variabele niet hoeft te herschrijven voordat u evalueert. Dit zou nodeloze complicaties introduceren.
   • $\ displaystyle \ start aligned \ frac 1 4 \ int _ 3 ^ 5 (u-3) \ sqrt u \ mathrm d u & = \ frac 1 4 \ int _ 3 ^ 5 (u ^ 3/2 -3u ^ 1/2) \ mathrm d u \ & = \ frac 1 4 \ left (\ frac 2 5 u ^ 5/2 -3 \ cdot \ frac 2 3 u ^ 3/2 \ right) \ Bigg | _ 3 ^ 5 \ & = \ frac 1 4 \ left (\ frac 2 5 (5) ^ 5 / 2 -2 \ cdot (5) ^ 3/2 - \ frac 2 5 (3) ^ 5/2 +2 \ cdot (3) ^ 3/2 \ right ) \ & = \ frac 1 4 \ left (- \ frac 6 5 \ cdot 3 ^ 3/2 +2 \ cdot 3 ^ 3/2 \ rechts) \ & = \ frac 1 4 \ frac 4 5 3 ^ 3/2 \ & = \ frac 3 \ sqrt 3 5 \ end gericht$

Part Seven of Seven:
Integratie door onderdelen

1. 1 Zie het hoofdartikel over hoe te integreren door delen. De integratie volgens de onderdelenformule wordt hieronder gegeven. Het belangrijkste doel van integratie door delen is om het product van twee functies te integreren - vandaar dat het de analoog is van de productregel voor derivaten. Deze techniek vereenvoudigt de integraal in een die hopelijk gemakkelijker te evalueren is.
   • $\ displaystyle \ int u \ mathrm d v = uv- \ int v \ mathrm d u$
2. 2 Evalueer de integraal van de logaritmefunctie. We weten dat de afgeleide van $\ displaystyle \ ln x$ is $\ displaystyle \ frac 1 x,$ maar niet de antiderivative. Het blijkt dat deze integraal een eenvoudige toepassing van integratie door delen is.
   • $\ displaystyle \ int \ ln x \ mathrm d x$
3. 3 Kies een $\ displaystyle u$ en $\ displaystyle \ mathrm d v,$ en vind $\ displaystyle \ mathrm d u$ en $\ displaystyle v$. We kiezen $\ displaystyle u = \ ln x$ omdat het derivaat algebraïsch is en daarom gemakkelijker te manipuleren. Dan $\ displaystyle \ mathrm d v = \ mathrm d x.$ daarom $\ displaystyle \ mathrm d u = \ frac 1 x \ mathrm d x$ en $\ displaystyle v = x.$ Als we al deze in de formule vervangen, krijgen we het volgende.
   • $\ displaystyle \ int \ ln x \ mathrm d x = x \ ln x- \ int \ mathrm d x$
   • We hebben de integraal van een logaritme omgezet in de integraal van 1, wat triviaal is om te evalueren.
4. 4 Evalueren.
   • $\ displaystyle \ int \ ln x \ mathrm d x = x \ ln x-x + C$