Hoe Gaussische functies te integreren

De Gauss-functie $\ displaystyle f (x) = e ^ - x ^ 2$ is een van de belangrijkste functies in de wiskunde en de wetenschappen. De karakteristieke klokvormige grafiek komt overal vandaan, van de normale verdeling in statistieken tot positie-golfpakketten van een deeltje in de kwantummechanica.

Het integreren van deze functie over alle $\ displaystyle x$ is een extreem veel voorkomende taak, maar het weerstaat de technieken van elementaire calculus. Geen enkele hoeveelheid verandering van variabelen, integratie door onderdelen, trigonometrische substitutie, enz. Zal de integraal vereenvoudigen. In feite kan het antiderivaat van de Gauss, de foutfunctie, niet worden geschreven in termen van elementaire functies. Niettemin bestaat er een exacte oplossing voor de definitieve integraal, die we in dit artikel vinden. We generaliseren ook de Gausse integrale om wat interessantere resultaten te verkrijgen. Deze generalisaties vereisen wat meer technieken zoals differentiëren onder de integraal en kennis van de Gamma-functie.

Deel een van de drie:
Gaussian Integraal

1. 1 Begin met de integraal.
   • $\ displaystyle \ int _ - \ infty ^ \ infty e ^ - x ^ 2 \ mathrm d x$
2. 2 Overweeg het vierkant van de integraal. We breiden deze integraal uit in de $\ displaystyle xy$ vlak. Het idee hier is om van dit probleem een ​​dubbele integraal te maken, die we gemakkelijk kunnen oplossen en vervolgens de wortel kunnen nemen.
   • $\ displaystyle \ int _ - \ infty ^ \ infty \ mathrm d xe ^ - x ^ 2 \ int _ - \ infty ^ \ infty \ mathrm d ye ^ - y ^ 2$
3. 3 Converteren naar poolcoördinaten. Herinner dat de gebiedsintegraal van een polaire rechthoek van de vorm is $\ displaystyle r \ mathrm d r \ mathrm d \ theta,$ met de extra $\ displaystyle r$ om de hoek te schalen naar eenheden van lengte. Deze extra $\ displaystyle r$ maakt de integralen triviaal aangezien we ons kunnen identificeren $\ displaystyle r ^ 2 = x ^ 2 + y ^ 2.$
   • $\ displaystyle \ start aligned \ int _ - \ infty ^ \ infty \ mathrm d xe ^ - x ^ 2 \ int _ - \ infty ^ \ infty \ mathrm d ye ^ - y ^ 2 & = \ int _ - \ infty ^ \ infty \ mathrm d x \ int _ - \ infty ^ \ infty \ mathrm d ye ^ - (x ^ 2 + y ^ 2) \ & = \ int _ 0 ^ \ infty r \ mathrm d r \ int _ 0 ^ 2 \ pi \ mathrm d \ theta e ^ - r ^ 2 \ end aligned$
4. 4 Evalueer door middel van een u-substitutie. Laat $\ displaystyle u = r ^ 2.$ Dan is het differentieel $\ displaystyle \ mathrm d u = 2r \ mathrm d r$ zal de extra annuleren $\ displaystyle r$ die we kregen van het veranderen naar polair. Omdat de integrand geen heeft $\ displaystyle \ theta$ afhankelijkheid, we kunnen de $\ displaystyle \ theta$ integraal meteen.
   • $\ displaystyle \ begin uitgelijnd \ int _ 0 ^ \ infty r \ mathrm d r \ int _ 0 ^ 2 \ pi \ mathrm d \ theta e ^ - r ^ 2 & = 2 \ pi \ int _ 0 ^ \ infty re ^ - r ^ 2 \ mathrm d r, \ quad u = r ^ 2 \ & = \ pi \ int _ 0 ^ \ infty e ^ - u \ mathrm d u \ & = \ pi (-e ^ - \ infty + e ^ 0) \ & = \ pi \ end aligned$
5. 5 Kom aan bij de integraal van een Gaussiaan. Omdat we het kwadraat van de integraal evalueerden, nemen we de vierkantswortel van ons resultaat.
   • $\ displaystyle \ int _ - \ infty ^ \ infty e ^ - x ^ 2 \ mathrm d x = \ sqrt \ pi$
   • Belangrijk is dat de Gauss-functie gelijk is.
     • $\ displaystyle \ int _ - \ infty ^ \ infty e ^ - x ^ 2 \ mathrm d x = 2 \ int _ 0 ^ \ infty e ^ -x ^ 2 \ mathrm d x = 2 \ cdot \ frac \ sqrt \ pi 2$
6. 6 Beschouw de integraal van de algemene Gauss-functie. Deze functie wordt bepaald door de parameters $\ displaystyle a$ en $\ displaystyle \ sigma,$ waar $\ displaystyle a$ is een (normalisatie) constante die de hoogte van de belcurve bepaalt, en $\ displaystyle \ sigma$ is de standaarddeviatie, die de breedte van de curve bepaalt.
   • $\ displaystyle f (x) = ae ^ - \ frac x ^ 2 2 \ sigma ^ 2$
   • Volg de bovenstaande stappen om deze integraal te verifiëren.
     • $\ displaystyle \ int _ - \ infty ^ \ infty ae ^ - \ frac x ^ 2 2 \ sigma ^ 2 \ mathrm d x = a \ sigma \ sqrt 2 \ pi$
   • Een andere manier om het probleem te formuleren is als we een Gaussiaanse vorm hebben $\ displaystyle e ^ - \ alpha x ^ 2.$ Controleer deze integraal ook.
     • $\ displaystyle \ int _ - \ infty ^ \ infty e ^ - \ alpha x ^ 2 \ mathrm d x = \ sqrt \ frac \ pi \ alpha$
7. 7 (Optioneel) Normaliseer het gebied om de normalisatieconstante te vinden $\ displaystyle a$. In veel toepassingen is het gewenst dat het gebied van de Gauss op één wordt ingesteld. In dit geval stellen we in $\ displaystyle a \ sigma \ sqrt 2 \ pi = 1$ en oplossen voor $\ displaystyle a.$
   • $\ displaystyle a = \ frac 1 \ sigma \ sqrt 2 \ pi$
   • Hier komen we aan bij de genormaliseerd Gaussiaans, zo gewenst in toepassingen als waarschijnlijkheidstheorie en kwantummechanica.
     • $\ displaystyle f (x) = \ frac 1 \ sigma \ sqrt 2 \ pi e ^ - \ frac x ^ 2 2 \ sigma ^ 2$

Tweede deel van de drie:
generalisaties

1. 1 Beschouw de integraal hieronder. De Gausse integrale $\ displaystyle \ int _ 0 ^ \ infty e ^ - \ alpha x ^ 2 \ mathrm d x = \ frac 1 2 \ sqrt \ frac \ pi \ alpha$ is een resultaat dat kan worden gebruikt om tal van gerelateerde integralen te vinden. De onderstaande worden gebeld momenten van de Gauss. hieronder $\ displaystyle n$ is een positief getal.
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ n e ^ - x ^ 2 \ mathrm d x$
2. 2 Als $\ displaystyle n$ is zelfs, denk aan de gerelateerde integraal (hieronder geschreven) en onderscheid onder de integraal. Het resultaat van differentiëren onder de integraal is dat zelfs krachten van $\ displaystyle x$ neergehaald worden. Merk op dat als de integraal wordt ontkend, het resultaat aan de rechterkant ook wordt genegeerd vanwege het negatieve vermogen in $\ displaystyle \ alpha,$ dus de antwoorden blijven positief. Omdat differentiatie veel eenvoudiger is dan integratie, kunnen we dit de hele dag doen, en zorgen dat we het instellen $\ displaystyle \ alpha = 1$ op een geschikt moment. We noemen een aantal van deze integralen hieronder. Zorg ervoor dat u ze zelf verifieert.
   • $\ displaystyle \ int _ 0 ^ \ infty e ^ - \ alpha x ^ 2 \ mathrm d x = \ frac 1 2 \ sqrt \ frac \ pi \ alpha$
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ 2 e ^ - x ^ 2 \ mathrm d x = - \ int _ 0 ^ \ infty \ frac \ partial \ partial \ alpha e ^ - \ alpha x ^ 2 \ mathrm d x = - \ frac \ mathrm d \ mathrm d \ alpha \ left (\ frac 1 2 \ sqrt \ frac \ pi \ alpha \ right) = \ frac \ sqrt \ pi 4$
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ 4 e ^ - x ^ 2 \ mathrm d x = \ frac 3 \ sqrt \ pi 8$
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ 6 e ^ - x ^ 2 \ mathrm d x = \ frac 15 \ sqrt \ pi 16$
3. 3 Als $\ displaystyle n$ is niet eens, gebruik de u-sub $\ displaystyle u = x ^ 2$. Dan kunnen we de Gamma-functie gebruiken om eenvoudig te evalueren. Hieronder kiezen we $\ displaystyle n = 9$ en $\ displaystyle n = 1/3$ als voorbeelden.
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ 9 e ^ - x ^ 2 \ mathrm d x = \ frac 1 2 \ int _ 0 ^ \ infty u ^ 4 e ^ - u \ mathrm d u = \ frac 4! 2 = 12$
   • $\ displaystyle \ int _ 0 ^ \ infty x ^ 1/3 e ^ - x ^ 2 \ mathrm d x = \ frac 1 2 \ int _ 0 ^ \ infty u ^ - 1/3 e ^ - u \ mathrm d u = \ frac \ Gamma (2/3) 2$
   • Het is interessant om op te merken dat we de Gamma-functie zelfs voor gebruik hadden kunnen gebruiken $\ displaystyle n$ ook. Het is een meer algemene methode voor het evalueren van dit soort integralen die doorgaans niet meer betrokken is dan differentiëren onder de integraal.
4. 4 set $\ displaystyle \ alpha = i$ om drie integralen te verkrijgen. Het resultaat is zo algemeen dat $\ displaystyle \ alpha$ kan zelfs complexe waarden aan, zolang als $\ displaystyle \ operatorname Re (\ alpha) \ geq 0.$ Herinner Euler's formule met betrekking tot de complexe exponentiële functie aan de trigonometrische functies. Als we de echte en imaginaire delen van ons resultaat nemen, krijgen we twee integralen gratis. Geen van de twee echte integralen heeft antiderivatieven die in gesloten vorm kunnen worden geschreven.
   • $\ displaystyle e ^ - ix ^ 2 = \ cos x ^ 2 -i \ sin x ^ 2$
   • $\ displaystyle \ int _ 0 ^ \ infty e ^ - ix ^ 2 \ mathrm d x = \ frac 1 2 \ sqrt \ frac \ pi i = \ frac \ sqrt \ pi 2 e ^ - i \ pi / 4 = \ frac \ sqrt \ pi 2 \ sqrt 2 (1-i)$
   • $\ displaystyle \ int _ 0 ^ \ infty \ cos x ^ 2 \ mathrm d x = \ int _ 0 ^ \ infty \ sin x ^ 2 \ mathrm d x = \ frac \ sqrt \ pi 2 \ sqrt 2$
   • Deze twee integralen zijn speciale gevallen van de Fresnel-integralen, waar ze belangrijk zijn in de studie van optica.
   • Als u niet erg vertrouwd bent met complexe getallen, het nummer $\ displaystyle i$ kan in polaire vorm worden herschreven als $\ displaystyle e ^ i \ pi / 2,$ omdat imaginaire exponenten rotaties zijn in het complexe vlak - in dit geval onder een hoek van $\ displaystyle \ pi / 2.$ De polaire vorm vereenvoudigt bijna alles wat met complexe getallen geassocieerd is, dus we kunnen gemakkelijk de vierkantswortel nemen.
5. 5 Bereken de Fourier-transformatie van de Gauss-functie door het vierkant te voltooien. Het berekenen van de Fourier-transformatie is rekenkundig heel eenvoudig, maar het vereist een kleine aanpassing. We kiezen ervoor om het vierkant te voltooien, omdat we de eigenschap herkennen die de integraal is onafhankelijk van de verschuiving (zie de discussie). Omdat we 0 moeten toevoegen om de integrand niet te wijzigen, moeten we compenseren door een $\ displaystyle - \ frac \ omega ^ 2 4$ termijn. Bekijk de borden - ze kunnen lastig zijn.
   • $\ displaystyle \ start aligned \ mathcal F \ e ^ - t ^ 2 \ & = \ int _ - \ infty ^ \ infty e ^ - t ^ 2 e ^ - i \ omega t \ mathrm d t \ & = \ int _ - \ infty ^ \ infty e ^ - (t ^ 2 + i \ omega t- \ omega ^ 2 / 4 + \ omega ^ 2 / 4) \ mathrm d t \ & = e ^ - \ omega ^ 2 / 4 \ int _ - \ infty ^ \ infty e ^ - (t + i \ omega / 2) ^ 2 \ mathrm d t \ & = \ sqrt \ pi e ^ - \ omega ^ 2 / 4 \ end aligned$
   • Interessant is dat de Fourier-transformatie van een Gauss een andere (geschaalde) Gaussiaanse is, een eigenschap die weinig andere functies hebben (de hyperbolische secant, waarvan de functie ook de vorm van een belkromme heeft, is ook zijn eigen Fourier-transformatie).
   • Deze techniek van het voltooien van het vierkant kan ook worden gebruikt om integralen zoals die hieronder te vinden. Controleer dit door de "gecomplexeerde" uitdrukking te beschouwen $\ displaystyle e ^ i \ alpha x / \ beta$ en dan het echte deel van het resultaat te nemen.
     • $\ displaystyle \ int _ - \ infty ^ \ infty \ cos \ frac \ alpha x \ beta e ^ - x ^ 2 \ mathrm d x = \ sqrt \ pi e ^ - \ alpha ^ 2 / 4 \ beta ^ 2$

Derde deel van de drie:
Foutfunctie

1. 1 Definieer de foutfunctie. Het is vaak het geval dat de Gausse integrale over de reële lijn moet worden geëvalueerd. Veel andere toepassingen, zoals in diffusie en statistieken, vereisen echter een meer algemene relatie.
   • Omdat de Gauss-functie geen antiderivatief heeft dat in termen van elementaire functies kan worden geschreven, definiëren we de foutfunctie $\ displaystyle \ operatorname erf (x)$ als het antiderivatief van de Gauss. Het is een speciale functie die conventioneel wordt gedefinieerd met een normalisatiefactor die een bereik van $\ displaystyle x \ in (-1,1).$ Het heeft een sigmavorm die qua vorm overeenkomt met de logistieke functie.
     • $\ displaystyle \ operatorname erf (x) = \ frac 2 \ sqrt \ pi \ int _ 0 ^ x e ^ - t ^ 2 \ mathrm d t$
   • Het is ook handig om de complementaire foutfunctie ook.
     • $\ displaystyle \ operatorname erfc (x) = 1- \ operatorname erf (x)$
   • Opgemerkt moet worden dat de handeling van het definiëren van deze speciale functie geen nieuwe inzichten of fundamentele invallen geeft in de wiskunde. Het is slechts een definitie van een functie die toevallig vaak genoeg wordt aangetroffen om een ​​eigen naam te krijgen.
2. 2 Los de eendimensionale warmtevergelijking op, gegeven de initiële condities. Als een voorbeeld van een toepassing die het gebruik van de foutfunctie vereist, lossen we de warmtevergelijking op met behulp van Fourier-transformaties, waarbij de beginvoorwaarden de rechthoekige functie zijn. hieronder $\ displaystyle \ alpha$ staat bekend als de diffusiecoëfficiënt.
   • $\ displaystyle \ frac \ partial u \ partial t - \ alpha \ frac \ partial ^ 2 u \ partial x ^ 2 = 0$
   • $\ displaystyle u (x, 0) = u_ 0 (x) = \ begin cases 1 & | x | \ leq 1/2 \ 0 & | x |> 1/2 \ end cases$
3. 3 Zoek de fundamentele oplossing. De fundamentele oplossing $\ displaystyle U (x, t)$ is de oplossing voor de warmtevergelijking gegeven beginvoorwaarden van een puntbron, de Dirac delta-functie. De fundamentele oplossing in deze context is ook bekend als de heat kernel.
   • We voeren een Fourier-transformatie uit om van echte ruimte naar om te zetten $\ displaystyle \ xi$ ruimte om een ​​gewone differentiaalvergelijking te verkrijgen $\ displaystyle t.$ Dan lossen we eenvoudig op voor $\ displaystyle \ hat u (\ xi, t).$ De nuttige eigenschap van de Fourier-transformatie die we hier gebruiken, is dat de Fourier-transformatie van een afgeleide van de orde $\ displaystyle n$ komt overeen met vermenigvuldiging van $\ displaystyle (i \ xi) ^ n$ in $\ displaystyle \ xi$ ruimte.
     • $\ displaystyle \ frac \ partial \ hat u \ partial t + \ alpha \ xi ^ 2 \ hat u = 0$
   • De extra constante komt eenvoudigweg overeen met de beginvoorwaarden.
     • $\ displaystyle \ hat u (\ xi, t) = \ hat u _ 0 (\ xi) e ^ - \ alpha \ xi ^ 2 t$
   • Nu moeten we terug transformeren in de echte ruimte. Dit is handig voor ons omdat vermenigvuldiging in $\ displaystyle \ xi$ ruimte komt overeen met convolutie in de echte ruimte. De fundamentele oplossing is dan simpelweg de inverse Fourier-transformatie van de exponentiële term, hieronder weergegeven. Het wordt als de fundamentele oplossing beschouwd omdat de deltafunctie de identiteitsoperator is van convolutie: $\ displaystyle \ delta (x) * U (x, t) = U (x, t).$
     • $\ displaystyle u (x, t) = u_ 0 (x) * \ mathcal F ^ - 1 \ left \ e ^ - \ alpha \ xi ^ 2 t \ right \$
   • We hebben al gezien hoe de Fourier-transformatie van een Gauss-functie te berekenen. We passen de techniek van het voltooien van het vierkant hier ook toe.
   • $\ displaystyle \ begin uitgelijnd U (x, t) & = \ mathcal F ^ - 1 \ left \ e ^ - \ alpha \ xi ^ 2 t \ right \ \ & = \ frac 1 2 \ pi \ int _ - \ infty ^ \ infty e ^ - \ alpha \ xi ^ 2 t e ^ ix \ xi \ mathrm d \ xi \ & = \ frac 1 2 \ pi \ int _ - \ infty ^ \ infty e ^ - \ alpha t \ left (\ xi ^ 2 -2 \ frac ix \ xi 2 \ alpha t - \ frac x ^ 2 4 \ alpha ^ 2 t ^ 2 \ right ) e ^ - x ^ 2 / 4 \ alpha t \ mathrm d \ xi \ & = \ frac 1 2 \ pi e ^ - x ^ 2 / 4 \ alpha t \ int _ - \ infty ^ \ infty e ^ - \ alpha t \ left (\ xi - \ frac ix 2 \ alpha t \ right) ^ 2 \ mathrm d \ xi \ & = \ frac 1 \ sqrt 4 \ pi \ alpha t e ^ - x ^ 2 / 4 \ alpha t \ end gericht$
4. 4 Oplossen voor $\ displaystyle u (x, t)$ gegeven beginvoorwaarden. Nu hebben we onze fundamentele oplossing $\ displaystyle U (x, t),$ we kunnen de convolutie van aannemen $\ displaystyle U (x, t)$ met $\ displaystyle u_ 0 (x).$
   • $\ displaystyle \ begin uitgelijnd u (x, t) & = u_ 0 (x) * U (x, t) = \ int _ - \ infty ^ \ infty u_ 0 ( y) U (xy, t) \ mathrm d y \ & = \ frac 1 \ sqrt 4 \ pi \ alpha t \ int _ - 1/2 ^ 1/2 e ^ - (xy) ^ 2 / 4 \ alpha t \ mathrm d y \ & = \ frac 1 \ sqrt 4 \ pi \ alpha t \ int _ - 1/2-x ^ 1/2-x e ^ - \ left (\ frac z \ sqrt 4 \ alpha t \ right) ^ 2 \ mathrm d z \ & = \ frac 1 2 \ left [\ operatorname erf \ left (\ frac 1/2-x \ sqrt 4 \ alpha t \ right) - \ operatorname erf \ left (\ frac -1 / 2-x \ sqrt 4 \ alpha t \ right) \ right] \ end uitgelijnde$
   • In de laatste stap maken we gebruik van het feit dat $\ displaystyle \ int e ^ - x ^ 2 \ mathrm d x = \ frac \ sqrt \ pi 2 \ operatorname erf (x).$
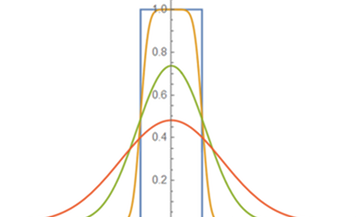
   • Een grafiek van deze functie in de tijd hierboven laat zien dat de "scherpte" van de functie na verloop van tijd afneemt en uiteindelijk neigt naar een evenwichtsoplossing. De beginvoorwaarden zijn in het blauw uitgezet, terwijl $\ displaystyle u (x, t)$ wordt geplot voor waarden $\ displaystyle t = 0.005,$ $\ displaystyle t = 0.1,$ en $\ displaystyle t = 0.3,$ voor respectievelijk oranje, groene en rode plots.
   • We zien aan de grafiek dat de functie dichtbij schuin afloopt $\ displaystyle x = \ pm 1/2,$ waarvoor de foutfunctie zorgt. De foutfunctie is echter nog steeds een continu, braaf functie, dus deze oplossing kan op dit moment niet bestaan $\ displaystyle t = 0,$ wanneer het argument binnen de foutfunctie enkelvoudig wordt en wanneer de functie de onderbreking $\ displaystyle u_ 0 (x)$ eerder gedefinieerd.