Hoe ombuigingspunten te vinden

In calculus is een buigpunt een punt op een curve waar de kromming van teken verandert. Het wordt gebruikt in verschillende disciplines, waaronder techniek, economie en statistiek, om fundamentele verschuivingen in gegevens te bepalen. Als u de buigpunten van een curve wilt vinden, gaat u naar deel 2.

Deel een van de drie:
Inflection Points begrijpen

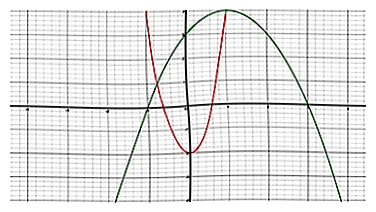
1. 1 Begrijp de concave up en concave down-functies. Om buigpunten te begrijpen, moet u een onderscheid maken tussen deze twee.
   • Een concave down-functie is een functie waarbij geen enkel lijnsegment dat twee punten op de grafiek met elkaar verbindt, ooit boven de grafiek uitkomt. Intuïtief heeft de grafiek de vorm van een heuvel.
   • Een concave up-functie daarentegen is een functie waarbij geen enkel lijnsegment dat twee punten op de grafiek met elkaar verbindt, ooit onder de grafiek uitkomt. Het heeft de vorm van een U.
   • In de bovenstaande grafiek is de rode curve hol omhoog, terwijl de groene curve hol omlaag is.
   • Functies in het algemeen hebben zowel concave omhooggaande als concave neerwaartse intervallen. Er zijn buigpunten wanneer een functie concaviteit verandert.
2. 2 Bekijk de wortels van een functie. Een wortel van een functie is het punt waarop de functie gelijk is aan nul. In de bovenstaande grafiek kunnen we zien dat de wortels van de groene parabool zich bevinden $\ displaystyle x = -1$ en $\ displaystyle x = 3.$ Dit zijn de punten waarop de functie de x-as snijdt.

Tweede deel van de drie:
De afgeleide producten van een functie vinden

1. 1 Differentiëren. Voordat u een buigpunt kunt vinden, moet u derivaten van uw functie zoeken. De afgeleiden van de basisfuncties zijn te vinden in elke calculustekst; je moet ze leren voordat je verder kunt gaan met meer complexe taken. Eerste derivaten worden aangeduid als $\ displaystyle f ^ \ prime (x)$ of $\ displaystyle \ frac \ mathrm d f \ mathrm d x.$
   • Stel dat je het buigpunt van de onderstaande functie moet vinden.
     • $\ displaystyle f (x) = x ^ 3 + 2x-1$
   • Gebruik de machtsregel.
     • $\ displaystyle \ begin uitgelijnd f ^ \ prime (x) & = 3x ^ 3-1 + 2x ^ 1-1 \ & = 3x ^ 2 +2 \ end aligned$
2. 2 Onderscheid opnieuw. Het tweede derivaat is het derivaat van het derivaat en wordt aangeduid als $\ displaystyle f ^ \ prime \ prime (x)$ of $\ displaystyle \ frac \ mathrm d ^ 2 f \ mathrm d x ^ 2.$
   • $\ displaystyle \ begin uitgelijnd f ^ \ prime \ prime (x) & = (2) (3) x ^ 2-1 \ & = 6x \ end aligned$
3. 3 Stel de tweede afgeleide gelijk aan nul en los de resulterende vergelijking op. Je antwoord is a mogelijk buigpunt.
   • $\ displaystyle \ start aligned 6x & = 0 \ x & = 0 \ end aligned$

Derde deel van de drie:
Een buigpunt vinden

1. 1 Controleer of het tweede afgeleide teken op het kandidaat-punt verandert. Als het teken van de tweede afgeleide verandert terwijl u het kandidaat-buigpunt passeert, bestaat er een buigpunt. Als het teken niet verandert, bestaat er geen buigpunt.
   • Houd er rekening mee dat u tekenwijzigingen zoekt en de waarde niet evalueert. In meer gecompliceerde uitdrukkingen kan substitutie ongewenst zijn, maar zorgvuldige aandacht voor tekens haalt vaak veel sneller het antwoord. Bijvoorbeeld, in plaats van cijfers onmiddellijk te evalueren, kunnen we in plaats daarvan naar bepaalde termen kijken en deze als positief of negatief beoordelen.
   • In ons voorbeeld $\ displaystyle f ^ \ prime \ prime (x) = 6x.$ Vervolgens een negatief aansluiten $\ displaystyle x$ levert een negatief op $\ displaystyle f ^ \ prime \ prime (x),$ terwijl je een positief aansluit $\ displaystyle x$ levert een positief op $\ displaystyle f ^ \ prime \ prime (x).$ daarom $\ displaystyle x = 0$ is een buigpunt van de functie $\ displaystyle f (x) = x ^ 3 + 2x-1.$ Het was niet nodig om daadwerkelijk te evalueren voor onze gekozen waarden.
2. 2 Vervangen door de oorspronkelijke functie.
   • $\ displaystyle f (0) = (0) ^ 3 +2 (0) -1 = -1.$
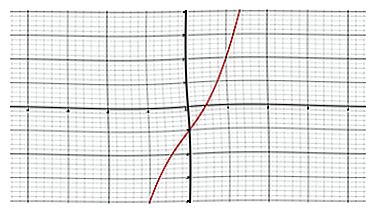3. 3 Zoek het buigpunt. De coördinaat van het buigpunt wordt aangeduid als $\ displaystyle (x, f (x)).$ In dit geval, $\ displaystyle (0, -1),$ zoals hierboven weergegeven.