Het delen door een decimaal getal kan in eerste instantie moeilijk lijken. Niemand onderwees je immers de '0.7 maal tafels'. Het geheim is om het delingprobleem te veranderen in een formaat dat alleen hele getallen gebruikt. Zodra je het probleem op deze manier hebt herschreven, wordt het een regulier langdelingsprobleem.
Deel een van de twee:
Het probleem schrijven als een gewone divisie Probleem
-
 1 Schrijf je verdeeldheidsprobleem op. Gebruik een potlood voor het geval u uw werk wilt herzien.
1 Schrijf je verdeeldheidsprobleem op. Gebruik een potlood voor het geval u uw werk wilt herzien. - Voorbeeld: Wat is 3 ÷ 1.2?
-
 2 Schrijf het hele getal als een decimaal. Schrijf een decimaalteken achter het hele getal, noteer nullen achter de komma. Doe dit totdat beide nummers hetzelfde aantal plaatsen rechts van de komma hebben. Dit heeft geen invloed op de waarde van het hele getal.
2 Schrijf het hele getal als een decimaal. Schrijf een decimaalteken achter het hele getal, noteer nullen achter de komma. Doe dit totdat beide nummers hetzelfde aantal plaatsen rechts van de komma hebben. Dit heeft geen invloed op de waarde van het hele getal. - Voorbeeld: In probleem 3 ÷ 1.2 is ons gehele getal 3. Omdat 1.2 één plaats rechts van de komma heeft, herschrijft u 3 als 3.0, dus het heeft ook één plaats na het decimaalteken. Nu is ons probleem 3.0 ÷ 1.2.
- Waarschuwing: voeg geen nullen toe links van de komma! 3 is hetzelfde als 3.0 of 3.00, maar dat is het wel niet hetzelfde als 30 of 300.
-
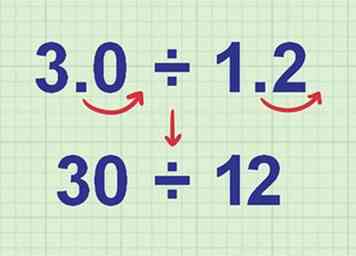 3 Verplaats de komma naar rechts tot je hele getallen hebt. Bij divisieproblemen mag u de komma's verplaatsen, maar enkel en alleen als je ze voor elk nummer met hetzelfde aantal verplaatst. Hiermee kunt u het probleem omzetten in hele getallen.
3 Verplaats de komma naar rechts tot je hele getallen hebt. Bij divisieproblemen mag u de komma's verplaatsen, maar enkel en alleen als je ze voor elk nummer met hetzelfde aantal verplaatst. Hiermee kunt u het probleem omzetten in hele getallen. - Voorbeeld: Als u 3.0 ÷ 1.2 in hele getallen wilt veranderen, verplaatst u de decimalen één vak naar rechts. 3.0 wordt 30 en 1.2 wordt 12. Nu is ons probleem 30 ÷ 12.
-
 4 Schrijf het probleem op met behulp van long division. Zet het dividend (meestal het grotere aantal) onder het langeafstandsymbool. Schrijf de deler erbuiten. Nu heb je een gewoon probleem met de lange divisie met hele getallen. Lees het volgende gedeelte als u een herinnering wilt hebben over hoe u long-division kunt doen.
4 Schrijf het probleem op met behulp van long division. Zet het dividend (meestal het grotere aantal) onder het langeafstandsymbool. Schrijf de deler erbuiten. Nu heb je een gewoon probleem met de lange divisie met hele getallen. Lees het volgende gedeelte als u een herinnering wilt hebben over hoe u long-division kunt doen.
Deel twee van twee:
Het probleem van de lange divisie oplossen
-
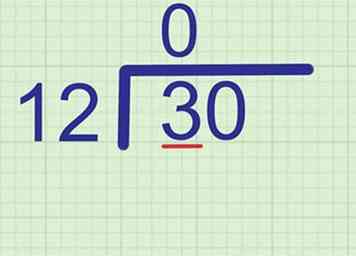 1 Zoek het eerste cijfer van het antwoord. Begin dit op te lossen, net zoals je normaal zou doen, door de deler te vergelijken met het eerste cijfer van het dividend. Bereken het aantal keren dat de deler naar dit cijfer gaat en schrijf dit getal boven dat cijfer.
1 Zoek het eerste cijfer van het antwoord. Begin dit op te lossen, net zoals je normaal zou doen, door de deler te vergelijken met het eerste cijfer van het dividend. Bereken het aantal keren dat de deler naar dit cijfer gaat en schrijf dit getal boven dat cijfer. - Voorbeeld: We proberen 12 in 30 te passen. Vergelijk 12 met het eerste cijfer van de deler, 3. Aangezien 12 groter is dan 3, gaat het er 0 keer in. Schrijven 0 boven de 3, op de antwoordregel.
-
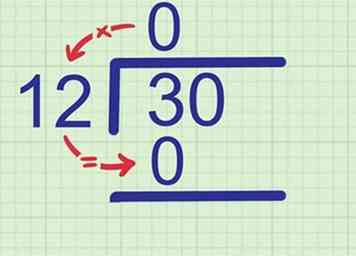 2 Vermenigvuldig dat cijfer met de deler. Schrijf het product (het antwoord op het vermenigvuldigingsprobleem) onder het dividend. Schrijf het direct onder het eerste cijfer van het dividend, omdat dit het cijfer is dat u zojuist hebt bekeken.
2 Vermenigvuldig dat cijfer met de deler. Schrijf het product (het antwoord op het vermenigvuldigingsprobleem) onder het dividend. Schrijf het direct onder het eerste cijfer van het dividend, omdat dit het cijfer is dat u zojuist hebt bekeken. - Voorbeeld: Aangezien 0 x 12 = 0, schrijf 0 onder de 3.
-
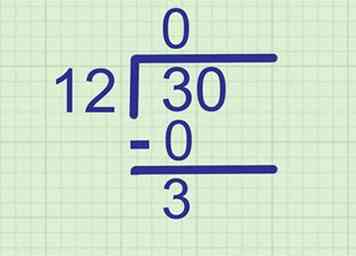 3 Trek af om te vinden wat er nog over is. Trek het product dat u zojuist hebt gevonden af van het cijfer er direct boven. Schrijf het antwoord op een nieuwe regel hieronder.
3 Trek af om te vinden wat er nog over is. Trek het product dat u zojuist hebt gevonden af van het cijfer er direct boven. Schrijf het antwoord op een nieuwe regel hieronder. - Voorbeeld: 3 - 0 = 3, dus schrijf 3 direct onder de 0.
-
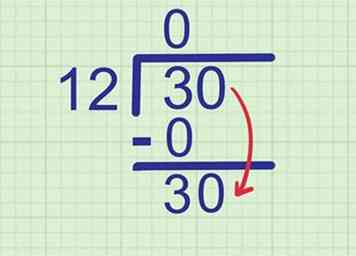 4 Breng het volgende cijfer naar beneden. Breng het volgende cijfer van het dividend naar beneden naast het nummer dat u zojuist hebt geschreven.
4 Breng het volgende cijfer naar beneden. Breng het volgende cijfer van het dividend naar beneden naast het nummer dat u zojuist hebt geschreven. - Voorbeeld: Ons dividend is 30. We hebben al naar de 3 gekeken, dus het volgende cijfer dat naar beneden gehaald moet worden is 0. Breng dit naast je 3 om te maken 30.
-
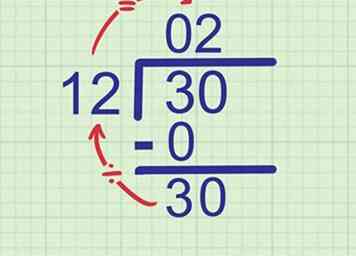 5 Probeer de deler in het nieuwe nummer te passen. Herhaal nu de eerste stap van dit gedeelte om het tweede cijfer van uw antwoord te vinden. Vergelijk deze keer met de deler met het nummer dat u zojuist op de onderste regel hebt genoteerd.
5 Probeer de deler in het nieuwe nummer te passen. Herhaal nu de eerste stap van dit gedeelte om het tweede cijfer van uw antwoord te vinden. Vergelijk deze keer met de deler met het nummer dat u zojuist op de onderste regel hebt genoteerd. - Voorbeeld:' Hoe vaak past 12 in 30? Het dichtst dat we kunnen krijgen is 2, omdat 12 x 2 = 24. Schrijf 2 op de tweede plaats van de antwoordregel.
- Als je niet zeker weet wat het antwoord is, probeer dan een aantal vermenigvuldigingsproblemen totdat je het grootste antwoord vindt dat past. Bijvoorbeeld, als het lijkt alsof 3 gaat over schrijven, vermenigvuldig dan 12 x 3 en je krijgt 36. Dit is te groot, omdat we proberen binnen 30 te passen. Probeer de volgende naar beneden, 12 x 2 = 24 Dit past wel, dus 2 is het juiste antwoord.
-
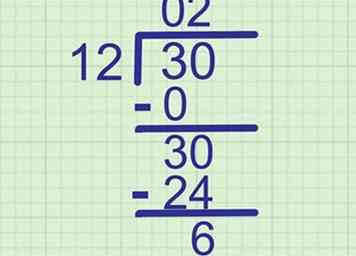 6 Herhaal de bovenstaande stappen om het volgende nummer te vinden. Dit is hetzelfde langeafstandsproces dat hierboven wordt gebruikt, en voor elk probleem van langdurige verdeeldheid:
6 Herhaal de bovenstaande stappen om het volgende nummer te vinden. Dit is hetzelfde langeafstandsproces dat hierboven wordt gebruikt, en voor elk probleem van langdurige verdeeldheid: - Vermenigvuldig het nieuwe cijfer op uw antwoordregel met de deler: 2 x 12 = 24.
- Schrijf het product op een nieuwe regel onder uw dividend: schrijf 24 direct onder de 30.
- Trek de onderste regel van de laag erboven af: 30 - 24 = 6, dus schrijf 6 op een nieuwe regel eronder.
-
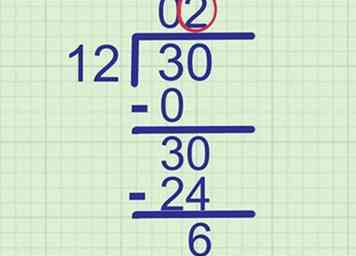 7 Ga door totdat je het einde van de antwoordregel hebt bereikt. Als er nog een cijfer in uw dividend zit, haal het dan naar beneden en blijf het probleem op dezelfde manier oplossen. Als je het einde van de antwoordregel hebt bereikt, ga je naar de volgende stap.
7 Ga door totdat je het einde van de antwoordregel hebt bereikt. Als er nog een cijfer in uw dividend zit, haal het dan naar beneden en blijf het probleem op dezelfde manier oplossen. Als je het einde van de antwoordregel hebt bereikt, ga je naar de volgende stap. - Voorbeeld: We hebben net geschreven 2 aan het einde van de antwoordregel. Ga naar de volgende stap.
-
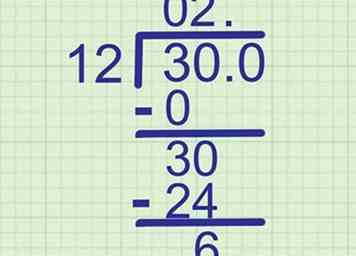 8 Voeg een decimaal toe om het dividend indien nodig te verlengen. Als de nummers gelijk verdeeld zijn, heeft uw laatste aftrekprobleem "0" als antwoord. Dat betekent dat je klaar bent, en je hebt een heel getal als antwoord op je probleem. Maar als u het einde van de antwoordregel hebt bereikt en er nog iets te splitsen is, moet u het dividend verlengen door een decimaalteken gevolgd door een 0 toe te voegen. Onthoud dat dit de waarde van het nummer niet verandert.
8 Voeg een decimaal toe om het dividend indien nodig te verlengen. Als de nummers gelijk verdeeld zijn, heeft uw laatste aftrekprobleem "0" als antwoord. Dat betekent dat je klaar bent, en je hebt een heel getal als antwoord op je probleem. Maar als u het einde van de antwoordregel hebt bereikt en er nog iets te splitsen is, moet u het dividend verlengen door een decimaalteken gevolgd door een 0 toe te voegen. Onthoud dat dit de waarde van het nummer niet verandert. - Voorbeeld: We zijn aan het einde van de antwoordregel, maar het antwoord op ons laatste aftrekklacht is "6." Verleng de "30" onder het langeafstandsymbool door ".0" aan het einde toe te voegen. Schrijf ook een decimaalteken op dezelfde plek op de antwoordregel, maar schrijf er nog niets achter.
-
 9 Herhaal dezelfde stappen om het volgende cijfer te vinden. Het enige verschil is dat u de komma naar dezelfde plek op de antwoordregel moet brengen. Als je dat eenmaal hebt gedaan, is het vinden van de resterende cijfers van het antwoord precies hetzelfde.
9 Herhaal dezelfde stappen om het volgende cijfer te vinden. Het enige verschil is dat u de komma naar dezelfde plek op de antwoordregel moet brengen. Als je dat eenmaal hebt gedaan, is het vinden van de resterende cijfers van het antwoord precies hetzelfde. - Voorbeeld: Breng de nieuwe 0 omlaag naar de laatste regel om "60" te maken. Aangezien 12 precies 5 keer in 60 gaat, schrijf 5 als het laatste cijfer op onze antwoordregel. Vergeet niet dat we een decimaal op onze antwoordregel plaatsen, dus 2.5 is het laatste antwoord op ons probleem.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Schrijf je verdeeldheidsprobleem op. Gebruik een potlood voor het geval u uw werk wilt herzien.
1 Schrijf je verdeeldheidsprobleem op. Gebruik een potlood voor het geval u uw werk wilt herzien.  2 Schrijf het hele getal als een decimaal. Schrijf een decimaalteken achter het hele getal, noteer nullen achter de komma. Doe dit totdat beide nummers hetzelfde aantal plaatsen rechts van de komma hebben. Dit heeft geen invloed op de waarde van het hele getal.
2 Schrijf het hele getal als een decimaal. Schrijf een decimaalteken achter het hele getal, noteer nullen achter de komma. Doe dit totdat beide nummers hetzelfde aantal plaatsen rechts van de komma hebben. Dit heeft geen invloed op de waarde van het hele getal. 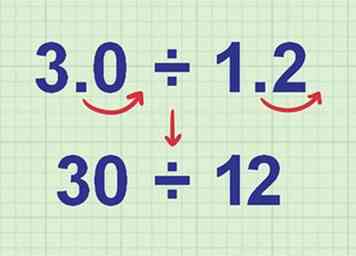 3 Verplaats de komma naar rechts tot je hele getallen hebt. Bij divisieproblemen mag u de komma's verplaatsen, maar enkel en alleen als je ze voor elk nummer met hetzelfde aantal verplaatst. Hiermee kunt u het probleem omzetten in hele getallen.
3 Verplaats de komma naar rechts tot je hele getallen hebt. Bij divisieproblemen mag u de komma's verplaatsen, maar enkel en alleen als je ze voor elk nummer met hetzelfde aantal verplaatst. Hiermee kunt u het probleem omzetten in hele getallen.  4 Schrijf het probleem op met behulp van long division. Zet het dividend (meestal het grotere aantal) onder het langeafstandsymbool. Schrijf de deler erbuiten. Nu heb je een gewoon probleem met de lange divisie met hele getallen. Lees het volgende gedeelte als u een herinnering wilt hebben over hoe u long-division kunt doen.
4 Schrijf het probleem op met behulp van long division. Zet het dividend (meestal het grotere aantal) onder het langeafstandsymbool. Schrijf de deler erbuiten. Nu heb je een gewoon probleem met de lange divisie met hele getallen. Lees het volgende gedeelte als u een herinnering wilt hebben over hoe u long-division kunt doen. 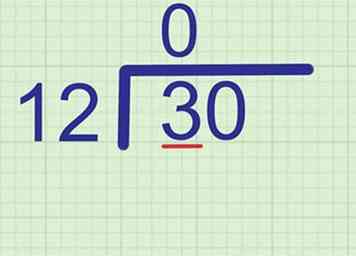 1 Zoek het eerste cijfer van het antwoord. Begin dit op te lossen, net zoals je normaal zou doen, door de deler te vergelijken met het eerste cijfer van het dividend. Bereken het aantal keren dat de deler naar dit cijfer gaat en schrijf dit getal boven dat cijfer.
1 Zoek het eerste cijfer van het antwoord. Begin dit op te lossen, net zoals je normaal zou doen, door de deler te vergelijken met het eerste cijfer van het dividend. Bereken het aantal keren dat de deler naar dit cijfer gaat en schrijf dit getal boven dat cijfer. 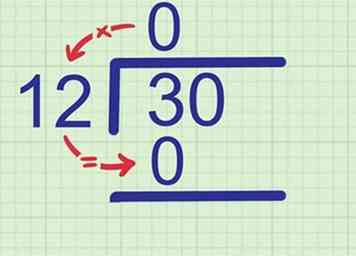 2 Vermenigvuldig dat cijfer met de deler. Schrijf het product (het antwoord op het vermenigvuldigingsprobleem) onder het dividend. Schrijf het direct onder het eerste cijfer van het dividend, omdat dit het cijfer is dat u zojuist hebt bekeken.
2 Vermenigvuldig dat cijfer met de deler. Schrijf het product (het antwoord op het vermenigvuldigingsprobleem) onder het dividend. Schrijf het direct onder het eerste cijfer van het dividend, omdat dit het cijfer is dat u zojuist hebt bekeken. 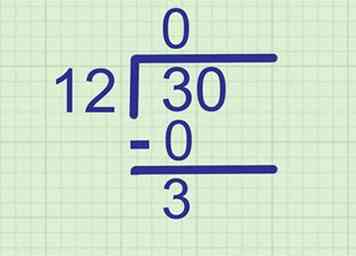 3 Trek af om te vinden wat er nog over is. Trek het product dat u zojuist hebt gevonden af van het cijfer er direct boven. Schrijf het antwoord op een nieuwe regel hieronder.
3 Trek af om te vinden wat er nog over is. Trek het product dat u zojuist hebt gevonden af van het cijfer er direct boven. Schrijf het antwoord op een nieuwe regel hieronder. 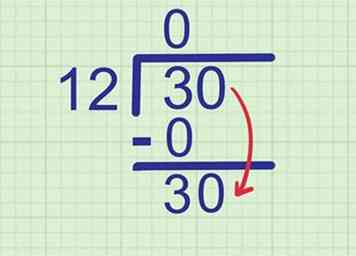 4 Breng het volgende cijfer naar beneden. Breng het volgende cijfer van het dividend naar beneden naast het nummer dat u zojuist hebt geschreven.
4 Breng het volgende cijfer naar beneden. Breng het volgende cijfer van het dividend naar beneden naast het nummer dat u zojuist hebt geschreven. 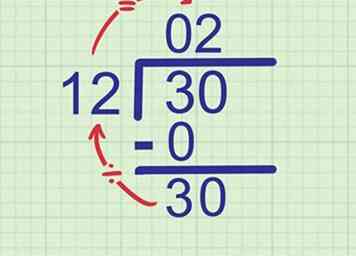 5 Probeer de deler in het nieuwe nummer te passen. Herhaal nu de eerste stap van dit gedeelte om het tweede cijfer van uw antwoord te vinden. Vergelijk deze keer met de deler met het nummer dat u zojuist op de onderste regel hebt genoteerd.
5 Probeer de deler in het nieuwe nummer te passen. Herhaal nu de eerste stap van dit gedeelte om het tweede cijfer van uw antwoord te vinden. Vergelijk deze keer met de deler met het nummer dat u zojuist op de onderste regel hebt genoteerd. 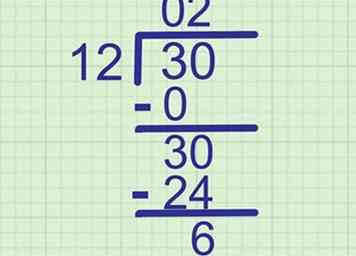 6 Herhaal de bovenstaande stappen om het volgende nummer te vinden. Dit is hetzelfde langeafstandsproces dat hierboven wordt gebruikt, en voor elk probleem van langdurige verdeeldheid:
6 Herhaal de bovenstaande stappen om het volgende nummer te vinden. Dit is hetzelfde langeafstandsproces dat hierboven wordt gebruikt, en voor elk probleem van langdurige verdeeldheid:  7 Ga door totdat je het einde van de antwoordregel hebt bereikt. Als er nog een cijfer in uw dividend zit, haal het dan naar beneden en blijf het probleem op dezelfde manier oplossen. Als je het einde van de antwoordregel hebt bereikt, ga je naar de volgende stap.
7 Ga door totdat je het einde van de antwoordregel hebt bereikt. Als er nog een cijfer in uw dividend zit, haal het dan naar beneden en blijf het probleem op dezelfde manier oplossen. Als je het einde van de antwoordregel hebt bereikt, ga je naar de volgende stap. 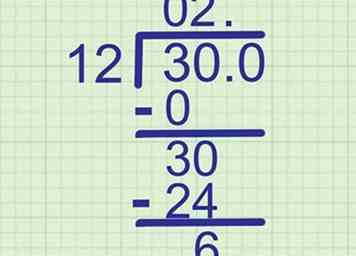 8 Voeg een decimaal toe om het dividend indien nodig te verlengen. Als de nummers gelijk verdeeld zijn, heeft uw laatste aftrekprobleem "0" als antwoord. Dat betekent dat je klaar bent, en je hebt een heel getal als antwoord op je probleem. Maar als u het einde van de antwoordregel hebt bereikt en er nog iets te splitsen is, moet u het dividend verlengen door een decimaalteken gevolgd door een 0 toe te voegen. Onthoud dat dit de waarde van het nummer niet verandert.
8 Voeg een decimaal toe om het dividend indien nodig te verlengen. Als de nummers gelijk verdeeld zijn, heeft uw laatste aftrekprobleem "0" als antwoord. Dat betekent dat je klaar bent, en je hebt een heel getal als antwoord op je probleem. Maar als u het einde van de antwoordregel hebt bereikt en er nog iets te splitsen is, moet u het dividend verlengen door een decimaalteken gevolgd door een 0 toe te voegen. Onthoud dat dit de waarde van het nummer niet verandert.  9 Herhaal dezelfde stappen om het volgende cijfer te vinden. Het enige verschil is dat u de komma naar dezelfde plek op de antwoordregel moet brengen. Als je dat eenmaal hebt gedaan, is het vinden van de resterende cijfers van het antwoord precies hetzelfde.
9 Herhaal dezelfde stappen om het volgende cijfer te vinden. Het enige verschil is dat u de komma naar dezelfde plek op de antwoordregel moet brengen. Als je dat eenmaal hebt gedaan, is het vinden van de resterende cijfers van het antwoord precies hetzelfde.